Übungsblatt zum Baumdiagramm

Übungsaufgaben zum Baumdiagramm und Pfadregeln

1. Regeln
1.1. Versuche die Verzweigungsregel mit eigenen Worten zu beschreiben!

1.2. Finde nun auch noch eigene Worte für die erste Pfadregel!

1.3. Fasse jetzt noch die zweite Pfadregel in eigene Worte!
weiter
2. Zuordnung von Bäumen.

2.1. Ein Zahlenschloss mit drei Wahlscheiben hat die Nummern 0-9. Die abgebildete richtige Zahlenkombination soll erraten werden. Wähle von folgenden Ereignisbäumen den richtigen aus und begründe deine Wahl.

a b

weiter

2.2. Ein Laplace-Würfel, der auf je zwei Seiten dieselbe Farbe hat wird dreimal hintereinander geworfen, welches ist der richtige Ereignisbaum?
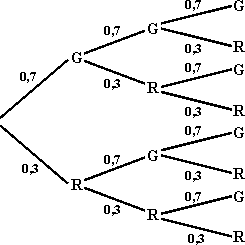
a

b

weiter

2.3. Im Losverfahren werden 3 von 15 Schüler ausgewählt, um zu ermitteln welche Schüler Referate halten dürfen, dabei wird die Reihenfolge mitbeachtet. Wähle ein geeignetes Baumdiagramm und begründe deine Wahl.

a

b

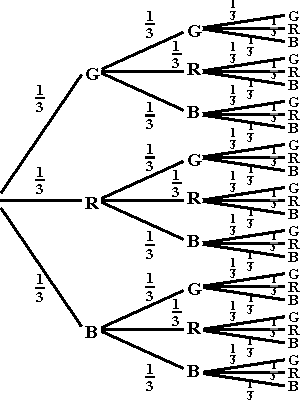
weiter
3. Zeichnen von einfachen Baumdiagrammen.
3.1. Ein Manager muss von München nach London fliegen.
Er hat zum einen die Möglichkeit den Flug A nach Hamburg zu nehmen, um anschließend mit der Maschine B bzw. mit dem Flugzeug C weiter zum Zielflughafen zu fliegen. Zum anderen kann er aber auch mit dem Flug X bis Amsterdam fliegen und von dort aus mit der Fluggesellschaft Y oder mit Z weiter bis zum Bestimmungsort.
Zeichne dafür einen passenden Ereignisbaum!
3.2. Auf dem Kurfürsten-Damm in Berlin werden des Nächtens illegale Gücksspiele abgehalten. Eines davon ist wie folgt: Auf einem Tisch befinden sich drei Becher, wobei sich unter einem von ihnen eine Holzkugel befindet. Wir bemühen uns zu glauben, dass alles mit rechten Dingen zugeht.
Darum zeichne ein Baumdiagramm, das symbolisiert, wie das Raten nach der Kugel ausfällt, nachdem zwei Spiele gemacht wurden. Gib die Einzelwahrscheinlichkeiten zu den Zweigen an!
3.3. (Etwas anspruchsvoller) Noch ein Spiel, jetzt jedoch mit traditionellen Schafkopf- Karten (32 Karten). Während dem Austeilen scheint es einem der vier Spieler, als bekäme er gute Karten für ein Herz Solo. Zu seinem Glück fehlt ihm nur noch eine Karte, der Alte (Eichel Ober). Es sind nun noch 12 Karten auszuteilen (pro Spieler 3x je eine Karte) und eine davon ist dieser Alte. Zeichne nun den Ereignisbaum, der darstellt, ob genannter Spieler seine Wunschkarte nach dem Austeilen bekommen bzw. nicht bekommen hat.

weiter Lösungen
4. Übungen zur ersten Pfadregel
Ein BOS Schüler geht 3mal in der Woche Schwimmen. Er hat jede Woche sieben frischgewaschene, unterschiedliche Handtücher, wobei zwei davon lediglich Gästehandtücher sind, die nur 30 x 30cm messen. Der Schüler greift immer ohne genau hinzusehen in seinen Kleiderschrank und eilt danach zum Schwimmbad. Da kommt es schon mal vor, dass er ein zu kleines Handtuch erwischt.
4.1. Zeichne einen passenden Ereignisbaum!
4.2. Danach berechne unter Anwendung der 1. Pfadregel die Wahrscheinlichkeit,...
4.2.1. ...mit der er nur am ersten Tag ein kleines Handtuch mitnimmt.
4.2.2. ...dass er nur am dritten Tag keines der grossen Handtücher dabei hat.
4.2.3. ...mit der er nur am zweiten Tag ein grosses Handtuch mit sich trägt.
4.2.4. ...dass er am ersten und am dritten Tag ein kleines Handtuch bei sich hat.
4.2.5. ...dass der Schüler sich an jedem der Tage mit einem richtig grossen Handtuch abtrocknen darf.

weiter Lösungen

5. Aufgaben zu beiden Pfadregeln.
Für den anspruchsvollen Schüler!
5.1. Zeichne für die abgebildete Urne ein Baumdiagramm, das ein dreimaliges ziehen darstellt.
5.2. Beschrifte die Pfade mit den Wahrscheinlichkeiten.
Die Kugeln werden nach dem Herausnehmen nicht wieder zurückgelegt.

5.3. Errechne die Wahrscheinlichkeiten sämtlicher Elementarereignisse unter Anwendung der ersten Pfadregel und notiere diese.
5.4. Berechne anhand des Ereignisbaumes die Wahrscheinlichkeiten für folgende Ereignisse:
5.4.1 P₁=({mindestens einmal R})
5.4.2 P₂=({höchstens einmal G})
5.4.3 P₃=({genau zweimal B})

ENDE

5. Aufgaben zu beiden Pfadregeln. Für den anspruchsvollen Schüler! 5.1. Zeichne für die abgebildete Urne ein Baumdiagramm, das ein dreimaliges ziehen darstellt. 5.2. Beschrifte die Pfade mit den Wahrscheinlichkeiten. Die Kugeln werden nach dem Herausnehmen nicht wieder zurückgelegt.
5.3. Errechne die Wahrscheinlichkeiten sämtlicher Elementarereignisse unter Anwendung der ersten Pfadregel und notiere diese. 5.4. Berechne anhand des Ereignisbaumes die Wahrscheinlichkeiten für folgende Ereignisse: 5.4.1 P₁=({mindestens einmal R}) 5.4.2 P₂=({höchstens einmal G}) 5.4.3 P₃=({genau zweimal B})