Wichtig zur Ermittlung der
Hoch-, Tief-, und Terrassenpunkte
1.Ableitung (Hoch-, Tief-, Terrassenpunkt)
|
Bedeutung: |
|
Wichtig zur Ermittlung der |
Hoch- / Tiefpunkt
 |
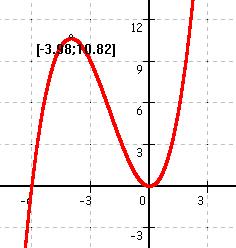Der Punkt (-3,98/10,82) ist der Hochpunkt (HOP) dieses Graphen. Der Punkt (0/0) ist der Tiefpunkt (TIP) des Graphen. |
Terrassenpunkt
 |
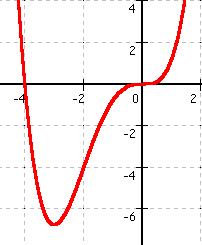Der Punkt (-3/-6,75) ist der Tiefpunkt des Graphen. Der Punkt (0/0) ist der Terrassenpunkt (TEP) des Graphen. |
Die HOP und TIP sind Extrempunkte und TEP hat ebenfalls eine horizontale Tangente, d. h. ....
Die
Berechnung der "Horizontalpunkte":
1. Schritt: ableiten !
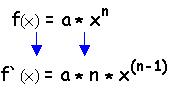
2. Schritt: Die Nullstellen der 1. Ableitung berechnen, da die Nullstellen der 1. Ableitung den X-Werten der Horizontalpunkte der Ursprungsfunktion entsprechen !
f'(x) = 0
3. Schritt: Ermittlung welche Art des Horizonzalpunktes vorliegt: Dazu nimmt man sich eine Monotonietabelle zur Hilfe.
Zur allgemeinen Erklärung seien
in diesem Fall x1, x2 und x3 die erhaltenen Nullstellen der 1. Ableitung!
|
|
x <
|
x1
|
< x <
|
x2
|
< x <
|
x3
|
< x
|
|
f'(x)
|
f'(x < x1) > 0
|
f'(x1) = 0
|
f'(x1 < x < x2) >
0
|
f'(x2) = 0
|
f'(x2 < x < x3) < 0
|
f'(x3) = 0
|
f'(x3 < x) > 0
|
|
|
|
|
|
|
|
|
|
|
|
das heißt:
der Wert von pos. Vorzeichen (+) |
|
das heißt: der Wert von f' pos. Vorzeichen (+) |
|
das heißt: der Wert von f' neg. Vorzeichen (-) |
|
das heißt: der Wert von f' pos. Vorzeichen (+) |
|
|
 |
|
|
|
|
|
|
|
|
das heißt: dass die |
|
das heißt: dass die Funktion |
|
das heißt: dass die |
|
das heißt: dass die Funktion |
|
|
|
|
|
|
|
|
|
|
|
|
Daran
kann man erkennen, dass es sich um einen TEP handelt. |
|
Daran
kann man erkennen, dass es sich um einen HOP handelt. |
|
Daran
kann man erkennen, dass es sich um einen TIP handelt. |
|
oder:
Man nimmt sich seine Formelsammlung zur Hand und entscheidet anhand folgender Gesetzmäßigkeiten, welche Art des Horizontalpunktes vorliegt:
f'(x) = 0 sowie f''(x) < 0 
Hochpunkt !
f'(x) = 0 sowie f''(x) > 0 Tiefpunkt !
f'(x) = 0 sowie f''(x) = 0 aber f'''(x) ist ungleich 0 Terrassenpunkt !