2. Ableitung (Wendepunkt)
 |
Bedeutung: |
 |
Wichtig zur Ermittlung der |
 |
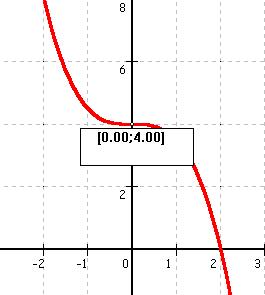Der Punkt (0/4) ist der Wendepunkt (WEP) dieses Graphen.
|
Der Wendepunkt ist der Punkt einer Funktion an dem sich das Krümmungsverhalten der Funktion ändert.
Zur
Berechnung des WEPs:
1. Schritt: Die 1. Ableitung der
Ursprungsfunktion ableiten !
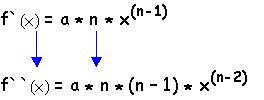
2. Schritt: Die Nullstellen der 2. Ableitung berechnen, da die Nullstellen der 2. Ableitung den X-Werten der Wendepunkte der Ursprungsfunktion entsprechen !
f''(x) = 0
3. Schritt: Nachweis des Wendepunkts durch eine Krümmungstabelle
Zur allgemeinen Erklärung sei in diesem Fall x1 die erhaltene Nullstelle der 2.Ableitung !
|
|
x <
|
x1
|
< x
|
|
f''(x)
|
f''(x < x1) > 0
|
f''(x1) = 0
|
f''(x1 < x) < 0
|
|
|
 |
|
|
|
|
das heißt: der Wert von f'' hat ein pos. Vorzeichen (+) |
|
das heißt: der Wert von f'' hat ein neg. Vorzeichen (-) |
|
|
|
|
|
|
|
das heißt: dass die Funktion in diesem Bereich linksgekrümmt ist |
|
das heißt: dass die Funktion in diesem Bereich rechtsgekrümmt ist |
oder:
Man nimmt sich seine Formelsammlung zur Hand und entscheidet anhand folgender Gesetzmäßigkeit, ob ein WEP vorliegt:
f''(x) = 0 und f'''(x) ungleich 0 
Wendepunkt !