| Grundbegriffe der Stochastik | Seminararbeit von Antje Lauber, November
2003 |
Definition:
und 
seien zwei Ereignisse desselben Egebnisraumes 
.
Gilt 
= 
,
d. h. die beiden Ereignisse schließen sich gegenseitig aus, so heißen
und
unvereinbare Ereignisse.
Gilt
,
d. h. die beiden Ereignisse schließen sich gegenseitig nicht aus, so heißen
und
vereinbare Ereignisse.
Betrachtet man zwei Ereignisse
und
eines Ergebnisraumes ,
so ist es wichtig zu wissen, ob beide Ereignisse gleichzeitig eintreten können
oder nicht.
Beispiel:
Es werden zwei unterscheidbare Würfel gewofen, die gefallenen Augenzahlen
werden notiert. Dabei betrachtet man folgende Ereignisse:
:
Augensumme weniger als 10; :
Augenprodukt gleich 20. Es ist zu untersuchen, ob beide Ereignisse gleichzeitig
eintreten können oder nicht.
Die Mengendarstellungen von
und lauten:
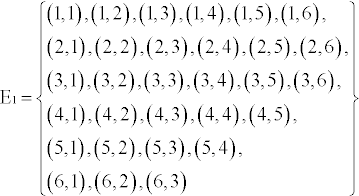
Offenbar können
und
gleichzeitig eintreten, nämlich dann, wenn bei Ausführung des Experimentes
z. B. das Ergebnis (4,5) auftritt. Die Ereignisse sind vereinbar.
Ändert man das zweite vorgegebne Ereignis ab in 
:
Augenprodukt gleich 24, so erhält man 
und sieht, daß jetzt
und
nicht gleichzeitig eintreten können. Dies liegt daran, daß hier
und
unvereinbare Ereignisse sind.
| << Ereignis |