Ein Ereignis A tritt ein, wenn das Ergebnis
eines Versuchs ein Element von A ist, also
A, es tritt nicht ein, wenn
kein Element von A ist, also
A. Die Menge aller Ereignisse aus 
heißt Ereignisraum P ().| Grundbegriffe der Stochastik | Seminararbeit von Antje Lauber, November
2003 |
Definition:
Ein Ereignis A tritt ein, wenn das Ergebnis
eines Versuchs ein Element von A ist, also
A, es tritt nicht ein, wenn
kein Element von A ist, also
A. Die Menge aller Ereignisse aus
heißt Ereignisraum P ().
Beispiel:
Der Ergebnisraum des Experiments "Zweimaliges Werfen einer Münze"
sei 
.
Gesucht ist der Ereignisraum P(),
also die Menge aller Teilmengen von .
Am übersichtlichsten ordnet man diese Teilmengen nach ihrer Mächtigkeit
und erhält dann:
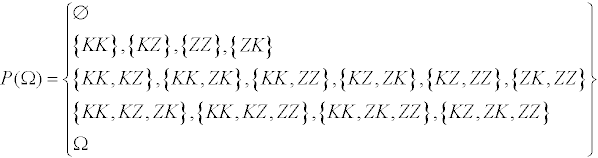
Ein Ereignisraum ist also immer eine Menge, deren Elemente selbst wiederum Mengen sind.
| << Ergebnis |
Ereignis >>
|