1.0
Gegeben sind die reellen Funktionen
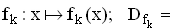 IR
IR
![]() mit k ≥ 0
mit k ≥ 0 ![]() k
k  IR .
IR .
Der Graph einer solchen Funktion f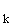 in einem kartesischen Koordinatensystem wird mit
in einem kartesischen Koordinatensystem wird mit ![]() bezeichnet.
bezeichnet.
1.1.1
Bestimmen Sie die Koordinaten des Wendepunktes W des Graphen
die Koordinaten des Wendepunktes W des Graphen 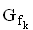 und begründen Sie, dass der Punkt W Wendepunkt eines jeden Graphen
und begründen Sie, dass der Punkt W Wendepunkt eines jeden Graphen ![]() ist . (Teilergebnis:
ist . (Teilergebnis: ![]() .) (4 BE)
.) (4 BE)
1.1.2
Ermitteln Sie in Abhängigkeit von k die maximalen Intervalle, in denen die Funktion fk echt monoton zunehmend ist.
1.1.3
Zeigen Sie, dass für einen geeigneten Wert von k die Gerade mit der Gleichung
dass für einen geeigneten Wert von k die Gerade mit der Gleichung 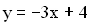 Wendetangente des zugehörigen Graphen
Wendetangente des zugehörigen Graphen ![]() ist. (3 BE)
ist. (3 BE)
1.2.0
Setzen Sie für die folgenden Teilaufgaben k = 3.
1.2.1
Bestimmen Sie die Nullstellen der Funktion 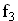 mit ihren Vielfachheiten und zerlegen Sie den Funktionsterm
mit ihren Vielfachheiten und zerlegen Sie den Funktionsterm 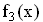 in Linearfaktoren. (7 BE)
in Linearfaktoren. (7 BE)
1.2.2
Geben Sie unter Verwendung bisheriger Ergebnisse Art und Koordinaten der relativen Extrempunkte des Graphen
unter Verwendung bisheriger Ergebnisse Art und Koordinaten der relativen Extrempunkte des Graphen 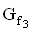 an und zeichnen Sie diesen Graphen für
an und zeichnen Sie diesen Graphen für 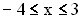 mit Hilfe einer geeigneten Wertetabelle.
mit Hilfe einer geeigneten Wertetabelle.
Maßstab auf beiden Achsen: 1 LE = 1 cm. (7 BE)
1.3.0
Die Parabel ![]() ist der Graph der quadratischen Funktion
ist der Graph der quadratischen Funktion ![]() ;
; ![]() IR . Die Funktion p hat bei x
IR . Die Funktion p hat bei x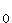 = –4 eine Nullstelle. Ihr Graph
= –4 eine Nullstelle. Ihr Graph ![]() schneidet den Graphen
schneidet den Graphen 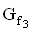 auf der y-Achse und hat in diesem Schnittpunkt die Steigung
auf der y-Achse und hat in diesem Schnittpunkt die Steigung 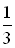 .
.
1.3.1
Bestimmen Sie den Funktionsterm p(x).
(Ergebnis: ![]() ) (6 BE)
) (6 BE)
1.3.2
Berechnen Sie die Koordinaten des Scheitelpunktes der Parabel ![]() und zeichnen Sie diese Parabel für
und zeichnen Sie diese Parabel für 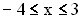 in das vorhandene Koordinatensystem ein. (4 BE)
in das vorhandene Koordinatensystem ein. (4 BE)
1.3.3
Die Parabel ![]() und der Graph
und der Graph 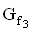 schließen im II. Quadranten des Koordinatensystems ein Flächenstück ein. Berechnen Sie seinen Flächeninhalt. (5 BE)
schließen im II. Quadranten des Koordinatensystems ein Flächenstück ein. Berechnen Sie seinen Flächeninhalt. (5 BE)
1.4.0
Gegeben ist nun die Funktion
nun die Funktion 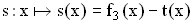 ;
; 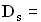 IR , wobei der Graph
IR , wobei der Graph 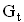 die Tangente an die Parabel
die Tangente an die Parabel 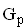 an der Stelle
an der Stelle 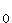 = –4
= –4
1.4.1
Zeigen Sie, dass sich der Funktionsterm s(x) in der Form
dass sich der Funktionsterm s(x) in der Form 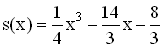 schreiben lässt.
schreiben lässt.
1.4.2
Begründen Sie, dass die Funktion s im Intervall [–1; 0] genau eine Nullstelle hat . (6 BE)
2.
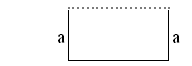 Im Geometrie-Unterricht der 5.Klasse findet ein "Wettbewerb" statt. Jedes der Kinder erhält ein Stück Draht der Länge 15 cm. Durch rechtwinkliges Aufbiegen je eines Stückes der Länge a an beiden Enden soll daraus ein U-förmiges Gebilde entstehen. Denkt man sich nun die beiden Drahtenden durch eine unsichtbare Linie verbunden, so erhält man ein Rechteck (siehe Skizze).
Im Geometrie-Unterricht der 5.Klasse findet ein "Wettbewerb" statt. Jedes der Kinder erhält ein Stück Draht der Länge 15 cm. Durch rechtwinkliges Aufbiegen je eines Stückes der Länge a an beiden Enden soll daraus ein U-förmiges Gebilde entstehen. Denkt man sich nun die beiden Drahtenden durch eine unsichtbare Linie verbunden, so erhält man ein Rechteck (siehe Skizze).
Sieger des Wettbewerbs ist dasjenige Kind, dessen Rechteck den größten Flächeninhalt hat.
2.1
Stellen Sie die Maßzahl A(a) der Rechtecksfläche in Abhängigkeit von a dar; bestimmen Sie die Definitionsmenge 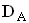 der Funktion A sinnvoll.
der Funktion A sinnvoll.
(Teilergebnis: 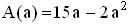 ) (4 BE)
) (4 BE)
2.2
Berechnen Sie denjenigen Wert von a, für den der Flächeninhalt den absolut größten Wert 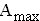 annimmt. Bestimmen Sie auch
annimmt. Bestimmen Sie auch 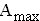 . (5 BE)
. (5 BE)
1.0
Gegeben sind die reellen Funktionen
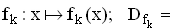 IR
IR
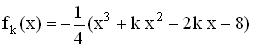 mit k
mit k  IR .
IR .
Der Graph einer solchen Funktion f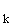 in einem kartesischen Koordinatensystem heißt
in einem kartesischen Koordinatensystem heißt 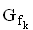 .
.
1.1.1
Zeigen Sie, dass x = 2 für alle Werte von k eine Nullstelle von f
= 2 für alle Werte von k eine Nullstelle von f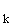 ist, und zerlegen Sie damit den Term
ist, und zerlegen Sie damit den Term ![]() in ein Produkt mit genau einem Linearfaktor. (5 BE)
in ein Produkt mit genau einem Linearfaktor. (5 BE)
(Mögliches Teilergebnis: ![]() )
)
1.1.2
Untersuchen Sie, für welche Werte von k die Funktion f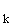 neben
neben  = 2
= 2
1.1.3
Berechnen Sie nun k so, dass die Funktion f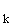 bei x
bei x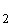 = –2 eine doppelte Nullstelle hat. (3 BE)
= –2 eine doppelte Nullstelle hat. (3 BE)
1.2.0
Für die Aufgaben dieser Gruppe gilt k = 2.
1.2.1
Bestimmen Sie Art und Koordinaten sämtlicher relativer Extrempunkte sowie die Koordinaten des Wendepunktes des Graphen 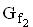 . (9 BE)
. (9 BE)
1.2.2
Zeichnen Sie den Graphen 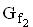 für –4 ≤ x ≤ 2,5. Verwenden Sie dazu die bisherigen Ergebnisse und berechnen Sie zusätzlich die Funktionswerte
für –4 ≤ x ≤ 2,5. Verwenden Sie dazu die bisherigen Ergebnisse und berechnen Sie zusätzlich die Funktionswerte 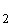 (–4)
(–4)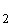 (0) und f
(0) und f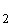 (2,5).
(2,5).
Maßstab auf beiden Achsen: 1 LE = 1 cm. (5 BE)
1.2.3
Der Graph 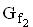 besitzt zwei Tangenten t
besitzt zwei Tangenten t und t
und t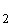 , die parallel zur Winkelhalbierenden des ersten und dritten Quadranten verlaufen. Die Berührpunkte dieser Tangenten mit dem Graphen
, die parallel zur Winkelhalbierenden des ersten und dritten Quadranten verlaufen. Die Berührpunkte dieser Tangenten mit dem Graphen 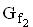 heißen B
heißen B und B
und B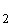 .
.
Der weiter rechts liegende Berührpunkt wird mit B bezeichnet.
bezeichnet.
Ermitteln Sie die Koordinaten der Punkte B und B
und B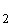 sowie die Gleichung der Tangente t
sowie die Gleichung der Tangente t .
.
(Teilergebnis: t hat die Funktionsgleichung y = x + 2) (7 BE)
hat die Funktionsgleichung y = x + 2) (7 BE)
1.2.4
Die Tangente t schließt mit dem Graphen
schließt mit dem Graphen 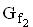 zwischen den Stellen
zwischen den Stellen 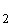 = –2
= –2 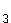 = 0
= 0  und
und 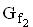 .)
.)
Zeichnen Sie die Gerade t in das vorhandene Koordinatensystem ein, schraffieren Sie das oben beschriebene Flächenstück und berechnen Sie die Maßzahl seines Flächeninhalts.
in das vorhandene Koordinatensystem ein, schraffieren Sie das oben beschriebene Flächenstück und berechnen Sie die Maßzahl seines Flächeninhalts.
1.3
Gegeben ist nun die reelle Funktion
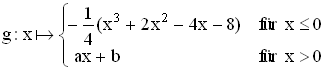 , a, b
, a, b  IR .
IR .
Berechnen Sie a und b so, dass die Funktion g an der Stelle x
Sie a und b so, dass die Funktion g an der Stelle x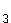 = 0 stetig und differenzierbar ist. (7 BE)
= 0 stetig und differenzierbar ist. (7 BE)
2.0
Ein Kino hat bei einem Eintrittspreis von DM 10,-- durchschnittlich 200 Besucher. Man schätzt, dass bei einer Erhöhung des Eintrittspreises um DM 1,-- die ursprüngliche Besucherzahl um durchschnittlich 10 abnehmen wird, bei einer Erhöhung um DM 2,-- um 20, bei einer Erhöhung um DM 3,-- um 30 usw.. (Zur Vereinfachung werden für die Berechnungen sämtliche Einheiten weggelassen.)
2.1
Die zu erwartenden Einnahmen in Abhängigkeit von der Preiserhöhung x lassen sich mit Hilfe einer differenzierbaren Funktion E beschreiben.
Ermitteln Sie den Funktionsterm E(x). Geben Sie auch eine sinnvolle Definitionsmenge 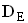 an, wenn man als Grundmenge IR wählt.
an, wenn man als Grundmenge IR wählt.
(Teilergebnis: 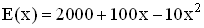 ) (4 BE)
) (4 BE)
2.2
Berechnen Sie den Eintrittspreis so, dass die Einnahmen den absolut größten Wert annehmen. (5 BE)
