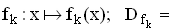 IR
IR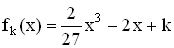 mit k
mit k  IR .
IR .Der Graph einer solchen Funktion wird mit
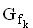 bezeichnet.
bezeichnet.1.1
Bestimmen Sie Art und Koordinaten sämtlicher Extrempunkte sowie die Koordinaten des Wendepunkts von
Sie Art und Koordinaten sämtlicher Extrempunkte sowie die Koordinaten des Wendepunkts von 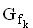 .
.
(Teilergebnisse: xT = 3; xH = –3) (9 BE)
1.2
Ermitteln Sie mit Hilfe der Extrempunkte aus Teilaufgabe 1.1 diejenigen Werte von k, für die die Funktion fk eine, zwei bzw. drei Nullstellen hat. (6 BE)
2.1
Die Funktion f5 (k = 5) besitzt genau eine Nullstelle (vgl. 1.2).
Zeigen Sie, dass sich diese Nullstelle zwischen x1 = –7 und x2 = –6 befindet.
Führen Sie für diese Nullstelle ausgehend vom Startwert x0 = –6,5 zwei Schritte des Newtonverfahrens durch. Geben Sie auch die für die Berechnung notwendigen Teilergebnisse an.
Runden Sie das Ergebnis auf zwei Nachkommastellen. (8 BE)
2.2
Zeichnen Sie den Graphen 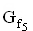 im Bereich –6,5 ≤ x ≤ 6,5 unter Berücksichtigung vorhandener Ergebnisse und unter Berechnung weiterer geeigneter Funktionswerte. Verwenden Sie ein gesondertes DIN-A4-Blatt im Hochformat und legen Sie den Koordinatenursprung in die Blattmitte.
im Bereich –6,5 ≤ x ≤ 6,5 unter Berücksichtigung vorhandener Ergebnisse und unter Berechnung weiterer geeigneter Funktionswerte. Verwenden Sie ein gesondertes DIN-A4-Blatt im Hochformat und legen Sie den Koordinatenursprung in die Blattmitte.
Maßstab auf beiden Achsen: 1 LE = 1 cm. (5 BE)
3.0
Die Parabel 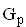 ist der Graph der quadratischen Funktion
ist der Graph der quadratischen Funktion 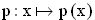 ;
; 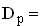 IR . Diese Parabel geht durch den Hochpunkt des Graphen
IR . Diese Parabel geht durch den Hochpunkt des Graphen 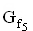 und berührt
und berührt 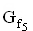 in dessen Tiefpunkt.
in dessen Tiefpunkt.
3.1
Bestimmen Sie den Funktionsterm p(x) und zeichnen Sie die Parabel 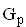 für –3 ≤ x ≤ 9 in das vorhandene Koordinatensystem ein. (8 BE)
für –3 ≤ x ≤ 9 in das vorhandene Koordinatensystem ein. (8 BE)
(Mögliches Teilergebnis: p(x) = 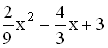 )
)
3.2.0
Gegeben sind die linearen Funktionen g mit g
mit g (x) = mx – 3m + 3;
(x) = mx – 3m + 3; 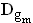 = IR
= IR IR.
IR.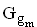 .
.
3.2.1
Zeigen Sie, dass die Parabel 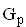 von jeder der Geraden
von jeder der Geraden 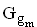 in zwei Punkten geschnitten wird. (4 BE)
in zwei Punkten geschnitten wird. (4 BE)
3.2.2
Bestimmen Sie für den Sonderfall m = 1 die x–Koordinaten der Schnittpunkte der Geraden
Sie für den Sonderfall m = 1 die x–Koordinaten der Schnittpunkte der Geraden 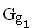 und der Parabel
und der Parabel 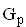 .
.
Zeichnen Sie die Gerade 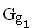 in das vorhandene Koordinatensystem ein und berechnen Sie den Inhalt des endlichen Flächenstücks, das diese Gerade und die Parabel
in das vorhandene Koordinatensystem ein und berechnen Sie den Inhalt des endlichen Flächenstücks, das diese Gerade und die Parabel 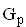 einschließen. (7 BE)
einschließen. (7 BE)
4.1
Betrachtet wird nun zusätzlich die Funktion
wird nun zusätzlich die Funktion 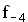 (k = –4). Begründen Sie kurz, wie der Graph
(k = –4). Begründen Sie kurz, wie der Graph 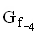 aus dem Graphen
aus dem Graphen 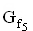 hervorgeht. Zeichnen Sie den Graphen
hervorgeht. Zeichnen Sie den Graphen 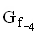 im Bereich
im Bereich 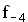 mit jeweiliger Vielfachheit an. (7 BE)
mit jeweiliger Vielfachheit an. (7 BE)
4.2
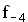 ist die Ableitungsfunktion einer Funktion
ist die Ableitungsfunktion einer Funktion 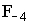 . Bestimmen Sie die maximalen Intervalle, in denen die Funktion
. Bestimmen Sie die maximalen Intervalle, in denen die Funktion 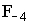 echt monoton zu- bzw. abnimmt. Geben Sie die x-Koordinaten sämtlicher Punkte an, in denen der Graph
echt monoton zu- bzw. abnimmt. Geben Sie die x-Koordinaten sämtlicher Punkte an, in denen der Graph 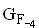 waagrechte Tangenten besitzt. Begründen Sie kurz, um welche Art Punkt es sich dabei jeweils handelt. (6 BE)
waagrechte Tangenten besitzt. Begründen Sie kurz, um welche Art Punkt es sich dabei jeweils handelt. (6 BE)

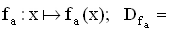 IR
IR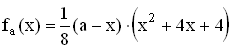 mit a
mit a 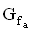 bezeichnet.
bezeichnet.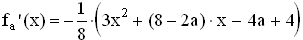 . )
. )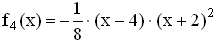 schreiben. (Beweis nicht erforderlich !)
schreiben. (Beweis nicht erforderlich !) .
.  ,
,  = IR
= IR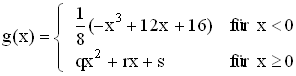 , mit q, r, s
, mit q, r, s  = 0 stetig und differenzierbar ist und der Graph G
= 0 stetig und differenzierbar ist und der Graph G
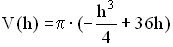 .) (4 BE)
.) (4 BE)