Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2003
Aufgabengruppe A: A I A II
A I
1.0
Die reelle Funktion 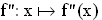 ;
;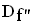 = IR
= IR
mit 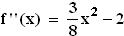
ist die zweite Ableitung der Funktion 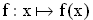 mit
mit 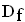 = IR .
= IR .
Der Graph der Funktion f wird mit 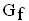 bezeichnet.
bezeichnet.
Gegeben ist außerdem die reelle Funktion p: x 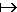 p(x);
p(x); 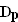 = IR
= IR
mit 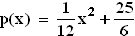 .
.
Der Graph dieser Funktion ist die Parabel 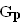 .
.
1.1
Der Graph 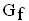 schneidet die Parabel
schneidet die Parabel 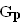 im Punkt A(2;
im Punkt A(2; 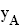 ). Die Steigung der Tangente an
). Die Steigung der Tangente an 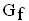 im Punkt A wird
im Punkt A wird 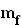 genannt, die Steigung der Tangente an
genannt, die Steigung der Tangente an 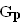 im selben Punkt
im selben Punkt 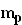 . Es gilt nun:
. Es gilt nun: 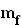 ·
· 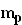 = –1. Berechnen Sie den Funktionsterm der Funktion f. (8 BE)
= –1. Berechnen Sie den Funktionsterm der Funktion f. (8 BE)
(Mögliches Ergebnis: 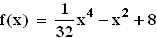 )
)
1.2
Untersuchen Sie den Graphen 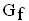 auf Symmetrie. (2 BE)
auf Symmetrie. (2 BE)
1.3
Berechnen Sie die Nullstellen der Funktion f. Geben Sie auch die zugehörigen Vielfachheiten an. (4 BE)
1.4
Ermitteln Sie Art und Koordinaten aller relativen Extrempunkte von 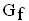 und geben Sie mit deren Hilfe die maximalen Intervalle an, in denen die Funktion f echt monoton zunimmt bzw. abnimmt. (8 BE)
und geben Sie mit deren Hilfe die maximalen Intervalle an, in denen die Funktion f echt monoton zunimmt bzw. abnimmt. (8 BE)
1.5
Bestimmen Sie die maximalen Intervalle, in denen der Graph rechts- bzw. linksgekrümmt ist sowie die Koordinaten der Wendepunkte. (7 BE)
1.6
Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter Funktionswerte die Graphen Gf und Gp für
Maßstab auf beiden Achsen: 1 LE = 1 cm. (8 BE)
1.7
Gf und Gp schließen miteinander 3 Flächenstücke ein. Berechnen Sie den Inhalt desjenigen Flächenstücks, das symmetrisch zur y-Achse liegt. (5 BE)
2.0
Eine Schnecke kriecht auf einer flachen Straße vom Startpunkt aus geradlinig immer in dieselbe Richtung. Modellhaft wird angenommen:
Die Funktion s: t 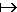
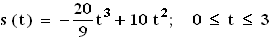
gibt den zurückgelegten Weg s (gemessen in Zentimetern) in Abhängigkeit von der Zeit t (gemessen in Minuten) wieder.
Die 1. Ableitung der Funktion s nach der Variablen t ist die Geschwindigkeit der Schnecke zum entsprechenden Zeitpunkt t.
(Auf Benennungen wird bei den folgenden Rechnungen verzichtet!)
2.1
Berechnen Sie den zurückgelegten Weg und die jeweilige Geschwindigkeit der Schnecke zu den Zeitpunkten
2.2
Ermitteln Sie, nach welcher Zeit die Schnecke ihre größte Geschwindigkeit erreicht hat. Wie groß ist diese maximale Geschwindigkeit? (4 BE)
3.0
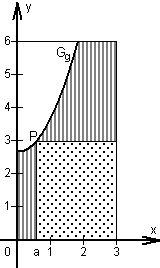
Die schraffierte Fläche in der nebenstehenden Skizze stellt den Rest einer längs eines Parabelstücks Gg zersprungenen ehemals rechteckigen Glasplatte dar. Der zu diesem Parabelstück gehörende Funktionsterm lautet:
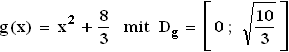 .
.
Aus dem Rest der Glasplatte soll eine achsenparallele Scheibe (punktiert) so geschnitten werden, dass der Punkt P(a; g(a)) auf Gg liegt.
3.1
Stellen Sie die Maßzahl A(a) der „neuen“ Rechtecksfläche in Abhängigkeit von der Abszisse a des Punktes P dar. Geben Sie auch eine sinnvolle Definitionsmenge DA an. (Lage von P siehe Skizze!) (4 BE)
(Mögliches Teilergebnis: 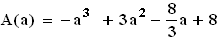 )
)
3.2
Bestimmen Sie nun denjenigen Wert von a, für den der Flächeninhalt den größten Wert Amax annimmt. Berechnen Sie auch Amax . (7 BE)
A II
1.0
Gegeben sind die reellen Funktionen
f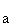 : x
: x 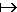 f
f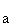 (x) ;
(x) ; 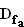 = IR
= IR
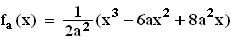 mit a
mit a  IR
IR 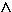 a > 0.
a > 0.
Der Graph einer solchen Funktion f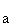 heißt
heißt 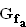 .
.
1.1
Begründen oder widerlegen Sie folgende Behauptung: Es gibt unter den Funktionen f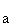 solche mit genau einer Nullstelle. (4 BE)
solche mit genau einer Nullstelle. (4 BE)
1.2
Zeigen Sie, dass der Wendepunkt eines jeden Graphen 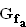 auf der x-Achse liegt und bestimmen Sie in Abhängigkeit von a die Gleichung der Wendetangente. (6 BE)
auf der x-Achse liegt und bestimmen Sie in Abhängigkeit von a die Gleichung der Wendetangente. (6 BE)
(Teilergebnis: xW = 2a )
1.3.0
In den folgenden Teilaufgaben ist a = 2.
1.3.1
Berechnen Sie alle Nullstellen der Funktion f2. (3 BE)
1.3.2
Ermitteln Sie die maximalen Intervalle, in denen die Funktion f2 echt monoton zunimmt bzw. abnimmt. Bestimmen Sie auf eine Nachkommastelle gerundet die Koordinaten der Extrempunkte und deren Art. (8 BE)
1.3.3
Zeichnen Sie unter Verwendung schon bekannter Werte und einer geeigneten Wertetabelle, die auch
Sie unter Verwendung schon bekannter Werte und einer geeigneten Wertetabelle, die auch 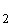 (–0,5)
(–0,5) 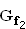 für –1 ≤ x ≤ 9.
für –1 ≤ x ≤ 9.
Maßstab auf beiden Achsen: 1 LE = 1 cm.
Verwenden Sie eine eigene Seite und legen Sie den Koordinatenursprung in die Blattmitte. (5 BE)
1.3.4
Tragen Sie in das Koordinatensystem von 1.3.3 die Wendetangente von 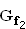 ein und kennzeichnen Sie die Fläche, die der Graph
ein und kennzeichnen Sie die Fläche, die der Graph 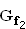 und seine Wendetangente mit der y-Achse einschließen. (2 BE)
und seine Wendetangente mit der y-Achse einschließen. (2 BE)
1.4
Berechnen Sie in Abhängigkeit von a > 0 die Maßzahl des Inhalts der Fläche, die die Wendetangente, der Graph
Sie in Abhängigkeit von a > 0 die Maßzahl des Inhalts der Fläche, die die Wendetangente, der Graph 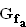 und die y-Achse einschließen. (5 BE)
und die y-Achse einschließen. (5 BE)
2.0
Der Graph der quadratischen Funktion p: x 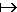 p(x);
p(x); 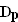 = IR, geht durch den Punkt A(–2; 3) und durch den Wendepunkt des Graphen
= IR, geht durch den Punkt A(–2; 3) und durch den Wendepunkt des Graphen 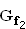 . Die Wendetangente von
. Die Wendetangente von 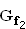 ist auch Tangente von
ist auch Tangente von 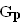 .
.
2.1
Bestimmen Sie den Funktionsterm p(x). (6 BE)
(Mögliches Ergebnis: p(x) = –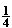 x
x + 4 )
+ 4 )
2.2
Zeigen Sie, dass die Graphen 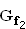 und
und 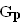 genau zwei gemeinsame Punkte aufweisen und geben Sie deren Koordinaten an. (7 BE)
genau zwei gemeinsame Punkte aufweisen und geben Sie deren Koordinaten an. (7 BE)
2.3
Zeichnen Sie die Parabel 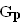 für –4 ≤ x ≤ 6 in das Koordinatensystem von Teilaufgabe 1.3.3 ein. (2 BE)
für –4 ≤ x ≤ 6 in das Koordinatensystem von Teilaufgabe 1.3.3 ein. (2 BE)
3.1
Eine natürliche Zahl heißt vollkommen, wenn sie gleich der Summe ihrer echten Teiler ist. Beispiel: 6 ist vollkommen, da
Zeigen Sie, dass auch 28 eine vollkommene Zahl ist. (2 BE)
3.2.0
Eine Fachoberschule beschließt, ein Denkmal zu errichten. Es soll die Form einer Pyramide mit quadratischer Grundfläche haben. Sie wird in der Hinsicht vollkommen sein, dass die Summe aus dem Umfang der Grundfläche und der Pyramidenhöhe 28 dm ergibt.
3.2.1
Bestimmen Sie das Volumen V(s) der Pyramide in Abhängigkeit von der Länge s einer Quadratseite und geben Sie eine sinnvolle Definitionsmenge DV an. (4 BE)
(Teilergebnis: V(s) = 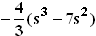 )
)
3.2.2
Berechnen Sie s so, dass das Pyramidenvolumen maximal wird. Geben Sie auch diesen maximalen Wert Vmax an. (6 BE)
