| 1.0 |
|
Gegeben sind die ganzrationalen Funktonen dritten Grades |
| |
|
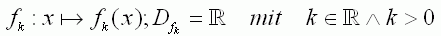 |
| |
|
| Der Graph einer solchen Funktion wird mit |
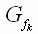 |
bezeichnet. |
|
|
|
|
|
|
(7 BE) |
| |
| 1.2 |
|
| Untersuchen Sie den Graphen |
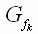 |
auf Symmetrie . |
|
|
|
(2 BE) |
| |
| 1.3 |
|
Ermitteln Sie Art und Koordinaten aller relativen Extrempunkte sowie das |
| |
|
| Krümmungsverhalten des Graphen |
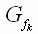 . . |
|
| |
|
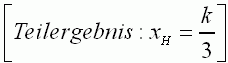 |
|
|
|
(8 BE) |
|
| 1.4 |
|
| Bestimmen Sie k so, dass der relative Hochpunkt des Graphen |
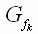 |
auf der |
|
| |
|
| Geraden g mit der Gleichung |
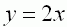 |
liegt. |
|
|
|
(3 BE) |
| |
| Für alle folgenden Teilaufgaben ist |
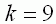 |
und somit |
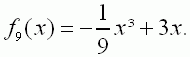 |
|
|
|
| 1.5 |
|
| Berechnen Sie die Nullstellen der Funktion |
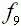 . . |
|
|
|
(3 BE) |
| |
| 1.6 |
|
Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter |
| |
|
| Funktionswerte den Graphen |
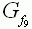 |
für |
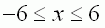 |
in ein Koordinatensystem. |
|
| |
|
Verwenden Sie eine eigene Seite. |
| |
|
Maßstab auf beiden Achsen: 1LE = 1cm. |
|
|
(6 BE) |
| |
| 2.1 |
|
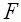 |
ist diejenige Stammfunktion der Funktion |
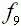 |
mit |
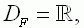 |
deren Graph |
|
| |
|
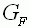 |
den Punkt |
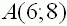 |
enthält. Bestimmen Sie den Funktionsterm |
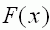 . . |
|
|
|
(3 BE) |
| |
| 2.2 |
|
Ermitteln Sie nur mit Hilfe bereits vorliegender Ergebnisse die maximalen |
| |
|
| Intervalle, in denen die Funktion |
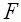 |
echt monoton zu- bzw. abnimmt. |
|
|
|
|
(4 BE) |
| |
| 2.3 |
|
| Der Graph |
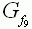 |
schließt mit der x-Achse zwei Flächenstücke ein. Berechnen Sie |
|
| |
|
deren Gesamtinhalt. |
|
|
(4 BE) |
| |
| 3.0 |
|
| Gegeben ist die Funktion |
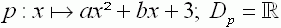 |
mit |
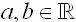 . . |
|
| |
|
| Der Graph der Funktion |
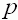 |
und |
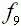 |
besitzen bei |
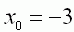 |
dieselbe Tangente. |
|
|
|
| 3.1 |
|
| Berechnen Sie den Funktionsterm |
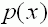 . . |
|
| |
|
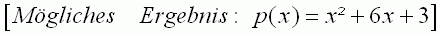 |
|
|
|
(5 BE) |
| |
|
|
|
(3 BE) |
| |
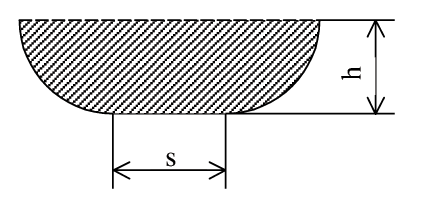
| 4.0 |
|
Der Querschnitt des abge- |
|
| |
bildeten, oben offenen Kanals |
| |
ist begrenzt durch zwei Vier- |
| |
telkrisbögen und durch eine |
| |
| Strecke der Länge |
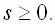 |
|
| |
| Die Höhe des Kanals ist |
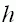 . . |
|
|
|
| 4.1 |
|
| Berechnen Sie den Inhalt der schraffierten Querschnittsfläche |
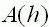 |
|
| |
|
in Abhängigkeit von der Höhe 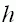 , wenn der „Umfang“ , wenn der „Umfang“ |
| |
|
(2 Viertelkreisbögen und Strecke s) 5 LE beträgt. |
| |
|
Ermitteln Sie die größtmögliche geometrisch sinnvolle Definitionsmenge der |
| |
|
| Funktion |
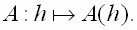 |
|
| |
|
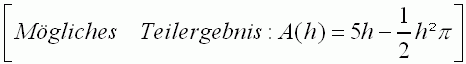 |
|
|
(7 BE) |
| |
|
|
|
(5 BE) |
| |
| |
 |
| |
| |
| |
| |
A II |
Seminararbeit von
Maria Mitterleitner
|
| |
| |
|
1.0 |
Gegeben sind die reellen Funktionen
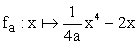 mit
mit
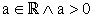 und
D und
D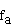 =
= 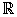 . .
Der Graph einer solchen Funktion wird mit
G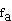 bezeichnet. bezeichnet.
|
|
1.1 |
Geben Sie das Verhalten der Funktionswerte für
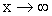 und und
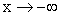 an. (2 BE) an. (2 BE)
|
|
1.2 |
Berechnen Sie die Nullstellen der Funktion
f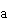 und geben Sie auch die
zugehörigen Vielfachheiten an. (4 BE) und geben Sie auch die
zugehörigen Vielfachheiten an. (4 BE)
|
|
1.3 |
Zeigen Sie rechnerisch, dass alle Graphen
G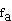 im Ursprung dieselbe Tangente besitzen. (3 BE)
im Ursprung dieselbe Tangente besitzen. (3 BE)
|
|
1.4 |
Berechnen Sie a so, dass der Graph
G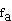 bei
x bei
x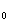 = 2 einen relativen Extrempunkt hat. = 2 einen relativen Extrempunkt hat.
Bestimmen Sie Art und Koordinaten dieses Extrempunkts. (5 BE)
|
Für alle folgenden Teilaufgaben ist a = 4 und
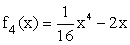
|
|
1.5 |
Ermitteln Sie das Krümmungsverhalten des Graphen
G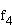 und untersuchen Sie, ob Wendepunkte vorliegen. (4 BE)
und untersuchen Sie, ob Wendepunkte vorliegen. (4 BE)
|
|
1.6 |
Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter Funktionswerte
den Graphen
G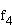 für für
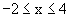 in ein Koordinatensystem. in ein Koordinatensystem.
Maßstab auf beiden Achsen: 1 LE= 1 cm. (5 BE)
|
|
1.7 |
Die Funktion F mit
D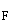 = =
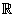 ist eine Stammfunktion von
f ist eine Stammfunktion von
f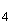 . .
Untersuchen Sie F auf Wendestellen, ohne F(x) zu berechnen. (3 BE)
|
|
1.8 |
Gegeben ist nun die abschnittsweise definierte Funktion |
|
g: x 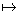
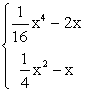
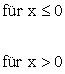
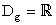
|
|
1.8.1 |
Weisen Sie nach, dass die Funktion g an der Nahtstelle stetig ist.
Untersuchen Sie anschließend rechnerisch, ob der Graph von g an dieser Stelle
„ohne Knick“ verläuft. (6 BE)
|
|
1.8.2 |
Zeichnen Sie den Graphen der Funktion g für
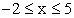 mit Farbe in das vorhandene
Koordinatensystem ein. (4 BE) mit Farbe in das vorhandene
Koordinatensystem ein. (4 BE)
|
|
1.9 |
Zwischen den Graphen G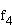 ,
G ,
G , der Geraden x = 2 und
dem Koordinatenursprung liegt im 4. Quadranten ein Flächenstück. , der Geraden x = 2 und
dem Koordinatenursprung liegt im 4. Quadranten ein Flächenstück.
Schraffieren Sie dieses Flächenstück und berechnen Sie die Maßzahl
des Flächeninhalts. (6 BE)
|
|
2.0 |
Untenstehende Skizze zeigt den Querschnitt einer
überdachten Wasserrutsche.
Der Graph
G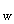 stellt die Wasserrutsche, der Graph
G
stellt die Wasserrutsche, der Graph
G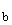 stellt die Bedachung dar,
stellt die Bedachung dar,
die über die Rutsche hinaus verlängert ist.
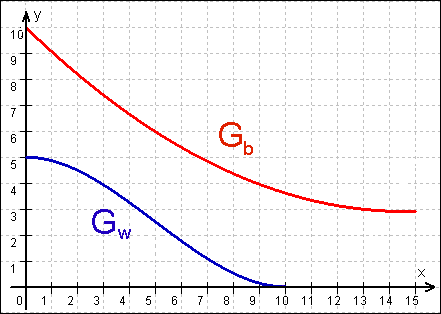
Die Funktionen w und b sind gegeben durch
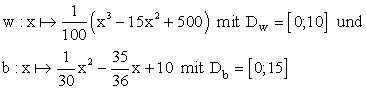
|
|
2.1 |
Berechnen Sie, an welcher Stelle
x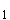 die Wasserrutsche das stärkste
Gefälle aufweist. (4 BE) die Wasserrutsche das stärkste
Gefälle aufweist. (4 BE)
|
|
2.2 |
Kondenswasser, das sich an der Unterseite der Bedachung gebildet
hat, tropft von der tiefsten Stelle des Daches herunter.
Berechnen Sie die Stelle
x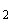 , an der das Wasser heruntertropft.
(4 BE) , an der das Wasser heruntertropft.
(4 BE)
|
|
2.3 |
Die Funktion d:x 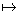 d(x) mit
D d(x) mit
D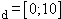 beschreibt den in y-Richtung
gemessenen
Abstand zwischen Wasserrutsche und Dach. beschreibt den in y-Richtung
gemessenen
Abstand zwischen Wasserrutsche und Dach.
Zeigen Sie, dass sich d(x) auch in der Form
d(x) = 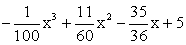 schreiben lässt. (2 BE) schreiben lässt. (2 BE)
|
|
2.4 |
Aus Sicherheitsgründen wird ein in y-Richtung gemessener
Mindestabstand zwischen Wasserrutsche und Dach von 3,30 (LE) vorgegeben. Untersuchen Sie
rechnerisch, ob dieser Mindestabstand an jeder Stelle eingehalten wird. (8 BE)
|
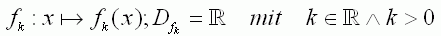
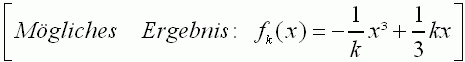
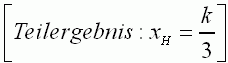
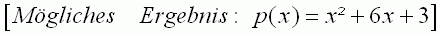
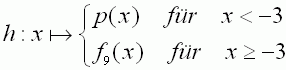
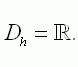
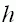 , wenn der „Umfang“
, wenn der „Umfang“ 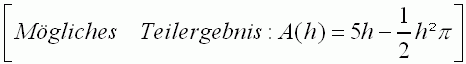
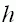 so, dass die Querschnittsfläche
so, dass die Querschnittsfläche 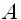 den größten Wert besitzt.
den größten Wert besitzt. 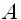 .
.
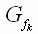
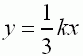
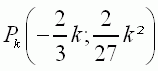 .
.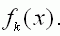
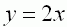
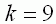
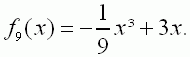
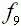 .
.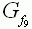
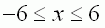
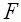
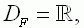
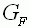
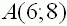
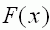 .
. 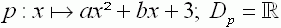
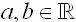 .
.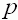
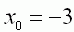
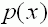 .
.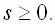
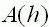
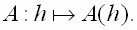
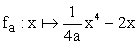 mit
mit
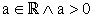 und
D
und
D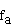 =
= 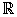 .
.
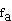 bezeichnet.
bezeichnet.
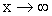 und
und
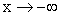 an. (2 BE)
an. (2 BE)
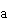 und geben Sie auch die
zugehörigen Vielfachheiten an. (4 BE)
und geben Sie auch die
zugehörigen Vielfachheiten an. (4 BE)
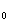 = 2 einen relativen Extrempunkt hat.
= 2 einen relativen Extrempunkt hat.
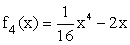
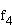 und untersuchen Sie, ob Wendepunkte vorliegen. (4 BE)
und untersuchen Sie, ob Wendepunkte vorliegen. (4 BE)
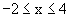 in ein Koordinatensystem.
in ein Koordinatensystem.
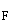 =
=
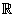 ist eine Stammfunktion von
f
ist eine Stammfunktion von
f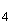 .
.
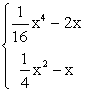
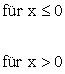
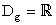
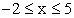 mit Farbe in das vorhandene
Koordinatensystem ein. (4 BE)
mit Farbe in das vorhandene
Koordinatensystem ein. (4 BE)
 , der Geraden x = 2 und
dem Koordinatenursprung liegt im 4. Quadranten ein Flächenstück.
, der Geraden x = 2 und
dem Koordinatenursprung liegt im 4. Quadranten ein Flächenstück.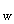 stellt die Wasserrutsche, der Graph
G
stellt die Wasserrutsche, der Graph
G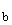 stellt die Bedachung dar,
stellt die Bedachung dar,

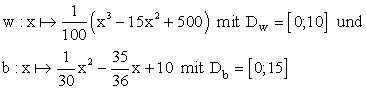
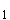 die Wasserrutsche das stärkste
Gefälle aufweist. (4 BE)
die Wasserrutsche das stärkste
Gefälle aufweist. (4 BE)
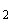 , an der das Wasser heruntertropft.
(4 BE)
, an der das Wasser heruntertropft.
(4 BE)
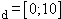 beschreibt den in y-Richtung
gemessenen
Abstand zwischen Wasserrutsche und Dach.
beschreibt den in y-Richtung
gemessenen
Abstand zwischen Wasserrutsche und Dach.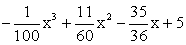 schreiben lässt. (2 BE)
schreiben lässt. (2 BE)