
Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2006
Aufgabengruppe A: A I A II
A I
Seminararbeit von Vanja Raicevic, Klasse 13f, Januar 2007



A II
Seminararbeit von Melanie Rothkegel, Klasse 13d, Januar 2007
1.0
Gegeben sind die reellen Funktionen ![]() und
und ![]() mit
mit ![]() .
.
1.1
Zeigen Sie, dass in der gesamten Definitionsmenge ![]() gilt und geben Sie die Bedeutung dieser Gleichung für den Graphen von
f an.
gilt und geben Sie die Bedeutung dieser Gleichung für den Graphen von
f an.
1.2
Bestimmen Sie die Nullstellen von f mit jeweiliger Vielfachheit.
1.3
Ermitteln Sie mit Hilfe der Ergebnisse von 1.1 und 1.2 Art und Koordinaten
sämtlicher Extrempkunkte des Graphen ![]() der Funktion g.
der Funktion g.
1.4
Berechnen Sie die Gleichung der Tangente an ![]() im Punkt
im Punkt ![]() .
.
1.5
Bestimmen Sie die maximalen Intervalle, in denen der Graph ![]() rechts- bzw. linksgekrümmt ist sowie die Koordinaten der Wendepunkte
rechts- bzw. linksgekrümmt ist sowie die Koordinaten der Wendepunkte
![]() und
und
![]() .
.
[Teilergebnis: ![]() ]
]
1.6
Zeichnen Sie den Graphen ![]() für
für ![]() in ein Koordinatensystem. Verwenden Sie dazu auch die Ergebnisse aus 1.l bis
1.5. Maßstab auf beiden Achsen: 1 LE = 1 cm.
in ein Koordinatensystem. Verwenden Sie dazu auch die Ergebnisse aus 1.l bis
1.5. Maßstab auf beiden Achsen: 1 LE = 1 cm.
1.7
Die Strecke [![]()
![]() ]
zwischen den beiden Hochpunkten (siehe 1.3) und der Graph von g begrenzen
ein Flächenstück. Berechnen Sie dessen Inhalt.
]
zwischen den beiden Hochpunkten (siehe 1.3) und der Graph von g begrenzen
ein Flächenstück. Berechnen Sie dessen Inhalt.
2.0
Gegeben ist die Funktion ![]() ;
;
![]() .
Ihr Graph
.
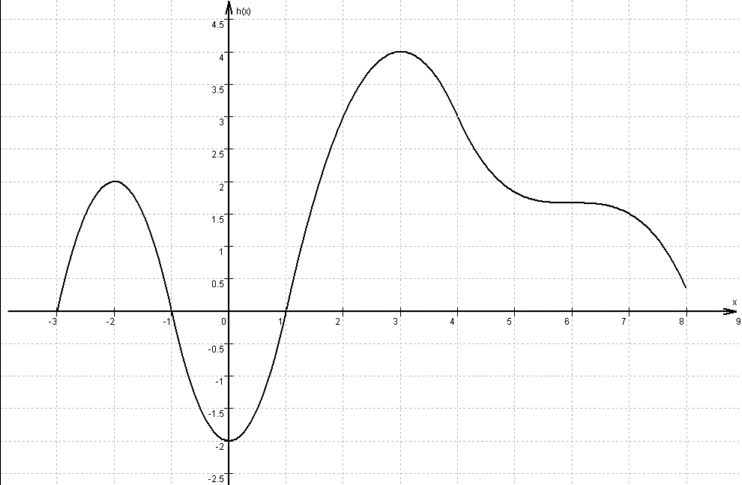
Ihr Graph ![]() hat folgendes Aussehen:
hat folgendes Aussehen:
2.1
Geben Sie die Nullstellen der Funktion h an.
2.2
An der Stelle 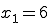 gilt
gilt ![]() ,
, ![]() ;
an der Stelle
;
an der Stelle 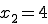 gilt
gilt ![]() ,
,
![]() . Geben Sie an, welcher Art die Punkte
. Geben Sie an, welcher Art die Punkte ![]() und
und ![]() demnach
sind.
demnach
sind.
2.3
Erläutern Sie kurz, was es jeweils für den Graphen ![]() bedeutet, wenn in einem bestimmten Intervall eine der Bedingungen
bedeutet, wenn in einem bestimmten Intervall eine der Bedingungen
| (A): |
(B): |
(C): |
gilt.
2.4
Geben Sie mit Hilfe der Zeichnung jeweils diejenigen Intervalle an, in denen
a) die Bedingungen (A) und (B) aus 2.3 zugleich,
b) alle 3 Bedingungen aus 2.3 zugleich gelten.
2.5
Im Intervall [-1 ; 4] lässt sich die Funktion h mit Hilfe von zwei ganzrationalen Termen 2. Grades darstellen. Geben Sie diese Darstellung in abschnittsweise definierter Form an.
3.0
Nebenstehendes Diagramm beschreibt den Zusammenhang zwischen der Momentangeschwindigkeit v(t) eines Fahrzeugs (in Kilometer pro Minute) und der Zeit t (in Minuten). (Auf Benennungen wird verzichtet!) |
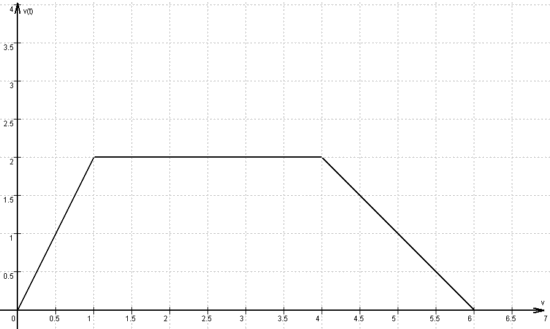 |
3.1
Begründen oder widerlegen Sie anhand des Diagramms die Behauptung:
Die Funktion v ist im dargestellten Bereich differenzierbar.
3.2
Geben Sie die Geschwindigkeiten zur Zeit ![]() und
und ![]() an.
an.
3.3
Die 1. Ableitung der Geschwindigkeit v(t) ist die Beschleunigung a(t) des Fahrzeugs.
Zeichnen Sie den Graphen der Funktion a.
3.4
Die Geschwindigkeit v(t) ist die 1. Ableitung der Funktion s(t), die den in der Zeit t zurückgelegten Weg beschreibt.
Bestimmen Sie mit Hilfe der Zeichnung den am Ende (nach 6 Minuten) zurückgelegten Weg.