| 1.0 |
Gegeben sind die reellen Funktionen 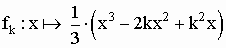 mit mit 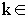 IR IR 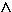 k ≥ 0 und k ≥ 0 und 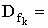 IR. Der Graph einer solchen Funktion wird mit IR. Der Graph einer solchen Funktion wird mit 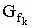 bezeichnet. bezeichnet. |
|
| 1.1 |
Berechnen Sie die Nullstellen der Funktion fk in Abhängigkeit von k. Geben Sie auch die zugehörigen Vielfachheiten an. |
(5 BE) |
| 1.2 |
Bestimmen Sie die maximalen Krümmungsintervalle von 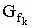 sowie mit deren Hilfe die Koordinaten des Wendepunktes. sowie mit deren Hilfe die Koordinaten des Wendepunktes.
[Teilergebnis: 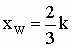 ] ] |
(6 BE) |
| 1.3 |
Bestimmen Sie die Gleichung der Wendetangente tk.
[Ergebnis: tk: y = 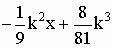 ] ]
|
(4 BE) |
| 1.4 |
Bestimmen Sie denjenigen Wert von 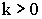 , für den der Inhalt des rechtwinkligen Dreiecks, das von der Wendetangente und den Koordinatenachsen begrenzt wird, 288 FE beträgt. , für den der Inhalt des rechtwinkligen Dreiecks, das von der Wendetangente und den Koordinatenachsen begrenzt wird, 288 FE beträgt. |
(6 BE) |
| 2.0 |
Nun sei k = 3. Man erhält die Funktion f3 mit 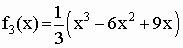 . . |
|
| 2.1 |
Ermitteln Sie die maximalen Intervalle, in denen die Funktion f3 echt monoton zunimmt bzw. abnimmt. Bestimmen Sie Art und Koordinaten aller relativen Extrempunkte des Graphen. |
(7 BE) |
| 2.2 |
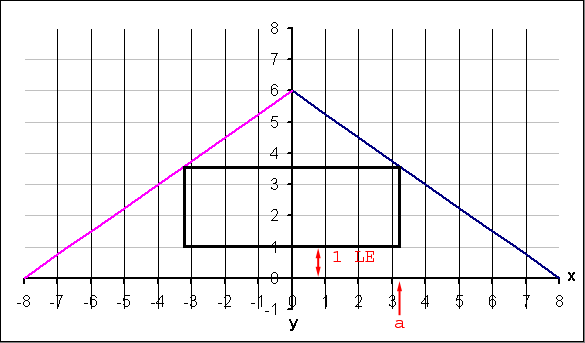
Zeichnen Sie unter Verwendung der bisherigen Ergebnisse und geeigneter Funktionswerte den Graphen der Funktion 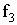 für –0,5 ≤ x ≤ 4 in ein Koordinatensystem. Zeichnen Sie auch den Wendepunkt und die Wendetangente ein. Maßstab: 1 LE = 2 cm. für –0,5 ≤ x ≤ 4 in ein Koordinatensystem. Zeichnen Sie auch den Wendepunkt und die Wendetangente ein. Maßstab: 1 LE = 2 cm. |
(5 BE) |
| 2.3 |
Der Graph 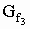 , die Wendetangente und die x-Achse schließen zwei Flächenstücke ein. Markieren Sie das größere der beiden im Koordinatensystem von Teilaufgabe 2.2 und berechnen Sie die Maßzahl des Flächeninhalts. , die Wendetangente und die x-Achse schließen zwei Flächenstücke ein. Markieren Sie das größere der beiden im Koordinatensystem von Teilaufgabe 2.2 und berechnen Sie die Maßzahl des Flächeninhalts. |
(8 BE) |
| 3.0 |
Für einen Snowboard-Sprungwettbewerb wird eine Rampe präpariert. Die Teilnehmer starten von einer waagrechten Plattform (AB), gleiten ab B(-5|4) ohne Knick durch die Rampe (BC) und beginnen den Sprung im Punkt C(0|0). Die Bahnkurve des Sprunges entspricht annähernd einer Parabel.
Skizze des Querschnitts, Flugbahn gestrichelt gezeichnet:
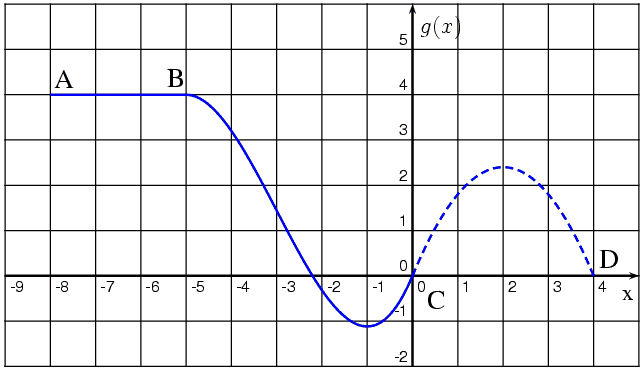
Der Querschnitt der Rampe (BC) kann durch die ganzrationale Funktion dritten Grades 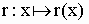 beschrieben werden mit Tiefpunkt beschrieben werden mit Tiefpunkt 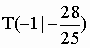 . . |
|
| 3.1 |
Ermitteln Sie den Funktionsterm r(x) dieser Funktion. |
(9 BE) |
| 3.2 |
Die Kurve aus obiger Skizze wird durch folgende abschnittsweise definierte Funktion beschrieben:
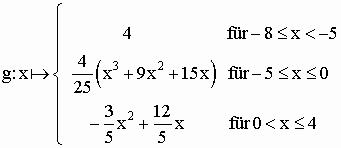
Die Funktion g ist stetig innerhalb ihrer gesamten Definitionsmenge (Nachweis nicht erforderlich). Begründen Sie rechnerisch, dass die Funktion an den Stellen x1 = –5 und x2 = 0 differenzierbar ist. |
(6 BE) |
| 3.3 |
Bestimmen Sie die Koordinaten desjenigen Punktes im abfallenden Teil der Rampe, in dem diese am steilsten ist. |
(4 BE) |
![]() mit
mit ![]() IR
IR 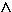 k ≥ 0 und
k ≥ 0 und ![]() IR. Der Graph einer solchen Funktion wird mit
IR. Der Graph einer solchen Funktion wird mit ![]() bezeichnet.
bezeichnet.
![]() beschrieben werden mit Tiefpunkt
beschrieben werden mit Tiefpunkt ![]() .
.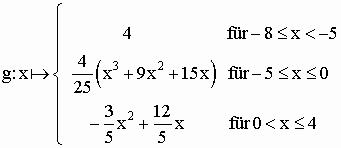

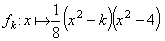
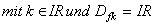 . Der Graph einer solchen Funktion wird mit
. Der Graph einer solchen Funktion wird mit 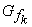 bezeichnet.
bezeichnet.