
Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2008
Aufgabengruppe A: A I A II
A I
Seminararbeit von Eva Henkel, Klasse 13a, Oktober 2008
Korrigiert von OStR Rudolf Litzberski




A II
Seminararbeit von Sarah Rabura Oktober 2008 Korrigiert von OStR Peter Starfinger |
||
1.0 |
Gegeben ist die reelle Funktion 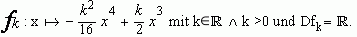
Der Graph wird mit 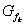 bezeichnet. bezeichnet. |
|
1.1 |
Bestimmen Sie Lage und Vielfachheit der Nullstellen der Funktion 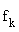 . .
Untersuchen Sie den Graphen 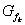 auf Symmetrie. auf Symmetrie. |
(5BE) |
1.2 |
Ermitteln Sie Art und Koordinaten des relativen Extrempunktes des Graphen 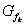 . .
Begründen Sie dann, dass dieser Extrempunkt für jeden Wert von k auf der Parabel 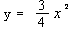 liegt. liegt.
 |
(8BE) |
2.0 |
Gegeben ist nun die reelle Funktion 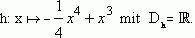
Der Graph dieser Funktion wird 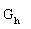 genannt. genannt. |
|
2.1 |
Begründen Sie kurz, dass 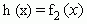 gilt und berechnen Sie dann für gilt und berechnen Sie dann für
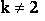 die x-Koordinaten der Schnittpunkte der Graphen die x-Koordinaten der Schnittpunkte der Graphen 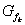 und und 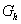 . . |
(7BE) |
2.2 |
Berechnen Sie die Koordinaten der Wendepunkte von 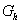 . Begründen Sie . Begründen Sie
auch, ob einer dieser Wendepunkte ein Terrassenpunkt ist. |
(6BE) |
2.3 |
Geben Sie die Nullstellen sowie die Koordinaten des Extrempunktes von 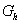
an und zeichnen Sie mit Hilfe vorliegender Ergebnisse und geeigneter Funktionswerte den Graphen 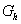 im Bereich im Bereich 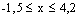 auf ein gesondertes auf ein gesondertes
DIN-A4-Blatt.( Koordinatenursprung auf der Seitenmitte, Maßstab auf beiden Achsen: 1 LE = 1 cm) |
(6BE) |
2.4 |
Der Graph 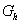 , die y-Achse und die Tangente im Hochpunkt des Graphen , die y-Achse und die Tangente im Hochpunkt des Graphen
schließen eine im I. Quadranten liegende Fläche ein. Kennzeichnen Sie diese Fläche im Koordinatensystem von Aufgabe 2.3 und berechnen Sie ihren Inhalt. |
(6BE) |
3.0 |
Gegeben ist nun die reelle Funktion 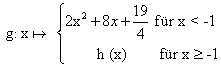
Begründen Sie rechnerisch, dass die Funktion g an der Stelle 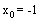
stetig und differenzierbar ist, und zeichnen Sie den Graphen dieser Funktion im Bereich 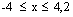 mit Farbe in das vorhandene Koordinatensystem mit Farbe in das vorhandene Koordinatensystem
ein. |
(9BE) |
4.0 |
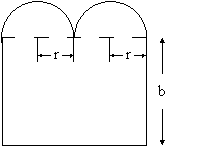 Ein Doppelrundbogenfenster
Ein Doppelrundbogenfenster
(siehe Zeichnung) wird von drei Seiten eines Rechtecks sowie von zwei Halbkreisen (jeweils Radius r) begrenzt. Der Umfang des Fensters be- trägt 10 m. (Auf Einheiten wird in der Rechnung verzichtet!) |
|
4.1 |
Stellen Sie den Flächeninhalt A(r) des Fensters in Abhängigkeit vom Radius r der Halbkreise dar und geben Sie eine sinnvolle Definitions- menge 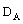 an. an.
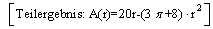 |
(7BE) |
4.2 |
Berechnen Sie auf 3 Nachkommastellen genau denjenigen Wert von r, für den der Flächeninhalt des Fensters seinen größten Wert annimmt. Wie viel Prozent des Inhalts nimmt in diesem Fall der rechteckige Teil des Fensters ein? |
(6BE) |