Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 1999
Aufgabengruppe A: A I A II
A I
1.0
Die reelle Funktion
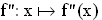 ;
; 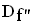 = IR
= IR
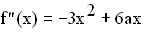 mit a
mit a  IR
IR
ist die zweite Ableitungsfunktion der Funktion 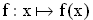 mit
mit 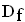 = IR . Der Graph der Funktion f in einem kartesischen Koordinatensystem heißt
= IR . Der Graph der Funktion f in einem kartesischen Koordinatensystem heißt 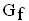 .
.
1.1.1
Der Graph 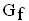 besitzt im Punkt P(2; 0) einen Wendepunkt. Die Tangente an diesen Graphen an der Stelle
besitzt im Punkt P(2; 0) einen Wendepunkt. Die Tangente an diesen Graphen an der Stelle 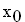 = 0 hat die Steigung m = –4.
= 0 hat die Steigung m = –4.
Bestimmen Sie den Funktionsterm f(x) der Funktion f. (6 BE)
(Ergebnis: 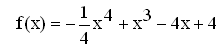 )
)
1.1.2
Ermitteln Sie Art und Koordinaten sämtlicher Wendepunkte des Graphen 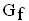 . (6 BE)
. (6 BE)
1.1.3
Bestimmen Sie die maximalen Intervalle, in denen die Funktion f echt monoton zu- bzw. abnimmt, sowie die Wertemenge 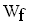 der Funktion f. (11 BE)
der Funktion f. (11 BE)
1.1.4
Zeichnen Sie den Graphen 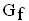 für –2 ≤ x ≤ 3. Verwenden Sie dazu die bisherigen Ergebnisse und berechnen Sie zusätzlich die Funktionswerte
für –2 ≤ x ≤ 3. Verwenden Sie dazu die bisherigen Ergebnisse und berechnen Sie zusätzlich die Funktionswerte
Maßstab: x-Achse: 1 LE = 2 cm; y-Achse: 1 LE = 1 cm.
1.2.0
Gegeben sind nun die reellen Funktionen
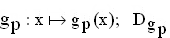 = IR
= IR
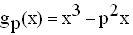 mit p
mit p  IR .
IR .
1.2.1
Untersuchen Sie den Graphen 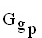 der Funktion
der Funktion 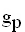 in Bezug auf Symmetrie und bestimmen Sie Anzahl und Lage sämtlicher Nullstellen der Funktion
in Bezug auf Symmetrie und bestimmen Sie Anzahl und Lage sämtlicher Nullstellen der Funktion 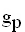 in Abhängigkeit von p. (7 BE)
in Abhängigkeit von p. (7 BE)
1.2.2
Für p > 0 schließt der Graph 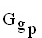 mit der x-Achse im IV. Quadranten ein endliches Flächenstück ein.
mit der x-Achse im IV. Quadranten ein endliches Flächenstück ein.
Berechnen Sie p > 0 so, dass die Maßzahl des zugehörigen Flächeninhalts den Wert 4 annimmt. (6 BE)
1.3.0
Für die folgenden Teilaufgaben sei p = 2.
1.3.1
Bestimmen Sie Art und Koordinaten der relativen Extrempunkte des Graphen 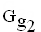 und zeichnen Sie diesen Graphen nur mit Hilfe bisheriger Ergebnisse für –2 ≤ x ≤ 2 in das vorhandene Koordinatensystem ein. (8 BE)
und zeichnen Sie diesen Graphen nur mit Hilfe bisheriger Ergebnisse für –2 ≤ x ≤ 2 in das vorhandene Koordinatensystem ein. (8 BE)
1.3.2
Die Graphen 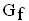 und
und 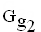 schließen ein endliches Flächenstück ein. Begründen Sie ohne Rechnung unter Verwendung bisheriger Ergebnisse und der Zeichnung, dass die Maßzahl des zugehörigen Flächeninhalts gleich
schließen ein endliches Flächenstück ein. Begründen Sie ohne Rechnung unter Verwendung bisheriger Ergebnisse und der Zeichnung, dass die Maßzahl des zugehörigen Flächeninhalts gleich 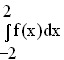 ist. (5 BE)
ist. (5 BE)
2.
Die Zahl 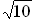 ist so in zwei reelle positive Summanden zu zerlegen, dass die Summe der Quadrate dieser Summanden einen absoluten Extremwert annimmt. Berechnen Sie die beiden Summanden und entscheiden Sie, welche Art von absolutem Extremum vorliegt. (6 BE)
ist so in zwei reelle positive Summanden zu zerlegen, dass die Summe der Quadrate dieser Summanden einen absoluten Extremwert annimmt. Berechnen Sie die beiden Summanden und entscheiden Sie, welche Art von absolutem Extremum vorliegt. (6 BE)
A II
1.0
Gegeben sind die reellen Funktionen
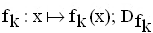 = IR
= IR
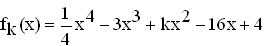 mit k
mit k  IR .
IR .
Der Graph einer solchen Funktion 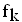 in einem kartesischen Koordinatensystem wird mit
in einem kartesischen Koordinatensystem wird mit 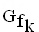 bezeichnet.
bezeichnet.
1.1
Begründen Sie mit Worten die folgende allgemeine Aussage: Ist 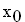 eine doppelte Nullstelle der zweiten Ableitung f '' einer ganzrationalen Funktion f, dann ist
eine doppelte Nullstelle der zweiten Ableitung f '' einer ganzrationalen Funktion f, dann ist 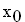 keine Wendestelle von f. (2 BE)
keine Wendestelle von f. (2 BE)
1.2
Bestimmen Sie die Anzahl und die Abszissen der Wendepunkte des Graphen 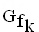 in Abhängigkeit von k. (8 BE)
in Abhängigkeit von k. (8 BE)
1.3
Berechnen Sie nun k so, dass der Graph 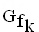 an der Stelle
an der Stelle 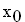 = 1 eine waagrechte Tangente besitzt. (2 BE)
= 1 eine waagrechte Tangente besitzt. (2 BE)
1.4.0
Für alle weiteren Teilaufgaben wird k = 12 gesetzt. Die Funktion 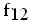 wird im Folgenden kurz mit f bezeichnet, ihr Graph mit
wird im Folgenden kurz mit f bezeichnet, ihr Graph mit 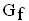 .
.
1.4.1
Ermitteln Sie Art und Koordinaten des relativen Extrempunktes sowie sämtlicher Wendepunkte des Graphen Gf . (12 BE)
1.4.2
Begründen Sie, dass die Funktion f zwischen den Stellen x1 = 0 und x2 = 1 genau eine Nullstelle besitzt.
Führen Sie ausgehend vom Startwert x1= 0 drei Schritte des Newtonverfahrens durch. Geben Sie auch die für die Berechnung notwendigen Teilergebnisse an. (10 BE)
1.4.3
Zeichnen Sie den Graphen 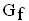 für 0 ≤ x ≤ 5. Verwenden Sie dazu die bisherigen Ergebnisse sowie die in Teilaufgabe 1.4.2 näherungsweise bestimmte Nullstelle und berechnen Sie zusätzlich die Funktionswerte f (3) und f (5). (5 BE)
für 0 ≤ x ≤ 5. Verwenden Sie dazu die bisherigen Ergebnisse sowie die in Teilaufgabe 1.4.2 näherungsweise bestimmte Nullstelle und berechnen Sie zusätzlich die Funktionswerte f (3) und f (5). (5 BE)
Maßstab auf beiden Achsen: 1 LE = 2 cm.
1.4.4
Die Gerade mit der Gleichung y = 4 schließt mit dem Graphen 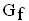 zwischen den Stellen x
zwischen den Stellen x = 0 und
= 0 und  = 4
= 4
2.
Gegeben ist nun die reelle Funktion
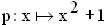 ;
; 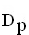 = { x
= { x  IR | x ≥ 0 }.
IR | x ≥ 0 }.
Bestimmen Sie diejenigen x-Werte mit x 
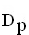 , für die gilt:
, für die gilt: 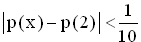 . (5 BE)
. (5 BE)
3.
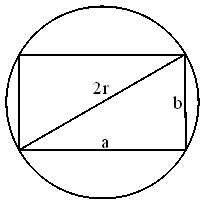 Aus einer kreisförmigen Rasenfläche mit dem Radius r = 5 (L.E.) soll für ein Blumenbeet eine rechteckige Fläche mit den Seiten a und b so ausgestochen werden, dass dieses Rechteck dem Kreis einbeschrieben ist (siehe Skizze). Die von a abhängige Maßzahl des Flächeninhalts des Rechtecks wird mit A(a) bezeichnet.
Aus einer kreisförmigen Rasenfläche mit dem Radius r = 5 (L.E.) soll für ein Blumenbeet eine rechteckige Fläche mit den Seiten a und b so ausgestochen werden, dass dieses Rechteck dem Kreis einbeschrieben ist (siehe Skizze). Die von a abhängige Maßzahl des Flächeninhalts des Rechtecks wird mit A(a) bezeichnet.
Berechnen Sie, wie lang die Seite a sein muss, damit die Größe g(a) = 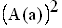 (und damit auch
(und damit auch
( Teilergebnis: g(a) = 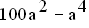 )
)
