Bei umfangreichen Verkehrszählungen in einer Großstadt wurden Zusammenhänge zwischen der Anzahl der vorbeifahrenden PKWs bzw. LKWs und dem Geschlecht der am Steuer sitzenden Personen festgestellt. Im Folgenden werden nur diese beiden Fahrzeugarten betrachtet. Die dabei ermittelten relativen Häufigkeiten werden als Wahrscheinlichkeiten interpretiert.
Nach dem Ergebnis der Zählungen handelt es sich bei 20% der betrachteten Fahrzeuge um LKWs. Je 31 von 100 der am Steuer eines Fahrzeugs sitzenden Personen sind weiblichen Geschlechts. Die Wahrscheinlichkeit, dass es sich bei einem zufällig herausgegriffenen Auto um einen von einer Dame gesteuerten PKW handelt, beträgt 0,28.
Folgende Bezeichnungen für Ereignisse werden festgelegt:
L:  "Das Fahrzeug ist ein LKW."
D:  "Das Fahrzeug wird von einer Dame gesteuert."

1.    

Zunächst werden die durch Verknüpfung der Ereignisse  L  und  D  entstandenen Ereignisse  A,  B  und  C  betrachtet:
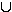
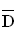a) A = L D;     b) B = L ;     c) C = .
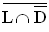Berechnen Sie die Wahrscheinlichkeiten der Ereignisse  A,  B  und  C,  z. B. mit Hilfe einer Vierfeldertafel, und formulieren Sie  A,  B  und  C  im Sinne der vorliegenden Thematik möglichst einfach mit Worten.   (8 BE)

2.

Weisen Sie rechnerisch nach, dass die Ereignisse  L  und  D  stochastisch abhängig sind.   (3 BE)

3.0

Nun wird eine Gruppe von drei aufeinander folgenden Fahrzeugen zufällig ausgewählt. Die Zufallsgröße  X  gibt die Anzahl der  PKWs  in dieser Gruppe an.
(Hinweis: Alle Wahrscheinlichkeiten sollen auf jeweils drei Stellen nach dem Komma angegeben werden.)

3.1

Zeichnen Sie für dieses Zufallsexperiment ein Baumdiagramm und geben Sie die Wahrscheinlichkeiten für die einzelnen Pfade an. Erstellen Sie ferner eine Wertetabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße  X  und zeichnen Sie dann ein zugehöriges Histogramm.   (7 BE)

3.2

Geben Sie für die zur Zufallsgröße  X  gehörige kumulative Verteilungsfunktion  F  eine Wertetabelle an und interpretieren Sie den Funktionswert  F(2) = 0,488.   (3 BE)

4.0

Nun wird eine Reihe von zehn hintereinander fahrenden Fahrzeugen betrachtet.

4.1

Berechnen Sie die Wahrscheinlichkeiten folgender Ereignisse:
E:   "Nur das fünfte Fahrzeug ist ein LKW."
E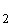:   "Genau die Hälfte der Fahrzeuge sind LKWs."
E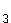:   "Die Fahrzeuge bilden eine 'bunte Reihe',
         d.h. abwechselnde Reihenfolge in Bezug auf die Fahrzeugart."
(Rechengenauigkeit bei P(E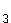): vier Nachkommastellen.)   (6 BE)

4.2

Bestimmen Sie die Wahrscheinlichkeit dafür, dass mindestens eines der zehn Fahrzeuge ein  LKW  ist.   (2 BE)

4.3

Berechnen Sie, welchen Wert die Wahrscheinlichkeit  p = P(L)  haben müsste, dass mit einer Wahrscheinlichkeit von  0,99  mindestens eines der zehn Fahrzeuge ein  LKW  wäre.   (4 BE)

5.

Zwei Jahre nach der Verkehrszählungsaktion äußern mehrere Mitglieder des Verkehrsausschusses die Vermutung, dass der Anteil der  LKWs  unter den betrachteten Fahrzeugen gegenüber der eingangs dargestellten Situation gestiegen sei (Gegenhypothese).
Es wird daraufhin ein Signifikanztest mit  200  zufällig ausgewählten Fahrzeugen vorgenommen. Dabei werden  45 LKWs  gezählt. Geben Sie für diesen Signifikanztest die Testgröße sowie die Nullhypothese an und bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem 5%-Niveau. Entscheiden Sie mit Hilfe dieses Tests, ob die Annahme, dass der Prozentsatz der  LKWs  nahezu gleich geblieben ist, als bestätigt angesehen werden kann oder nicht.   (7 BE)

1.0

Max Molle ist ein Junggeselle von 22 Jahren, der noch bei seinen Eltern wohnt. Wir treffen ihn gegen 18.00 Uhr auf einem Volksfest. An einer Schießbude gibt Herr Molle 8 Schüsse auf Papierblumen ab. Seine Trefferwahrscheinlichkeit pro Schuss beträgt konstant p = .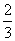
Herrn Molles Mutter hat heute ihren 46. Geburtstag und deshalb möchte er sie am Abend mit genau  6  Papierblumen überraschen. Bei mehr als  6  Treffern will er die übrigen Blumen der netten jungen Dame schenken, die er gerade kennen gelernt hat. Bei weniger als  6  Treffern soll diese neue Bekannte alle Blumen bekommen.
Bestimmen Sie jeweils auf  4  Nachkommastellen gerundet die Wahrscheinlichkeit dafür, dass

1.1

von Molles  8  Schüssen nur der erste und der letzte Schuss treffen;   (2 BE)

1.2

Herrn Molles Mutter heute ihre  6  Papierblumen erhält;   (3 BE)

1.3

die junge Dame mindestens eine Blume erhält.   (4 BE)

2.

Nach dem Schießen besucht Herr Molle mit der neuen Bekannten eine Bar und spielt dort ein Würfelspiel. Er wirft gleichzeitig zwei ideale, unterscheidbare Würfel.
Folgende Spielregel wird vereinbart:
Ist der Betrag der Differenz der geworfenen Augenzahlen gerade, so erhält Herr Molle den entsprechenden Betrag in DM von der Dame, bei einem ungeraden Differenzbetrag zahlt Herr Molle den entsprechenden Betrag in DM an diese.
Die Zufallsgröße  X  gibt den Gewinn (bzw. Verlust) von Herrn Molle bei einem solchen Spiel an.
Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße  X  in tabellarischer Form und zeichnen Sie mit Hilfe einer Wertetabelle den Graphen der kumulativen Verteilungsfunktion der Zufallsgröße  X.   (7 BE)

3.

Leider trinkt Herr Molle in der Bar ein paar Gläser Bier und daher möchte die junge Dame lieber gehen. Sie lässt sich jedoch überreden, ihre Entscheidung von einem weiteren Spiel abhängig zu machen: Herr Molle zieht aus einem gut durchmischten Kartenspiel (bestehend aus 32 Karten, darunter 4 Asse) ohne Zurücklegen zufällig nacheinander 10 Karten. Befindet sich unter diesen 10 Karten kein Ass, will die Dame noch etwas länger bleiben.
Berechnen Sie die Wahrscheinlichkeit dafür, dass die junge Dame aufgrund des Spielausgangs die Bar verlässt.   (4 BE)

4.0

Herrn Molle fällt um 22.00 Uhr der Geburtstag seiner Mutter wieder ein. Auf dem Heimweg kommt er noch einmal an der Schießbude vorbei.
Der Budenbesitzer behauptet, dass Molles Trefferwahrscheinlichkeit pro Schuss jetzt auf Grund seines inzwischen erhöhten Alkoholspiegels nicht mehr 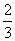beträgt, sondern dass sie größer oder kleiner geworden ist (Gegenhypothese). Herr Molle wettet, dass er weiterhin mit einer Wahrscheinlichkeit von 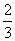trifft und bietet an, dies durch eine Testreihe von 30 Schuss nachzuweisen, bei denen er mindestens 18-, höchstens 22-mal treffen will.

4.1

Formulieren Sie Testgröße und Testart und geben Sie die Nullhypothese H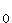 an sowie den Annahme- und den Ablehnungsbereich von H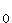. Berechnen Sie dann die Wahrscheinlichkeit dafür, dass Herr Molle seine Wette verliert, obwohl er immer noch mit einer Quote von 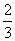trifft.   (6 BE)

4.2

Bestimmen Sie den kleinstmöglichen Annahmebereich der Nullhypothese symmetrisch zum Erwartungswert  20, der gewählt werden muss, wenn der Fehler 1. Art höchstens 5% beträgt.   (5 BE)

5.0

Ein neugieriger Nachbar von Herrn Molle führt schon seit längerem Aufzeichnungen über dessen abendliches Nachhausekommen. Kommt Herr Molle nach 22.00 Uhr heim, notiert der Nachbar dies als "Verspätung". Die Zufallsgröße  Y  gibt Herrn Molles Verspätungen in Stunden (gerundet) an. Es ergibt sich dabei mit a,  b  [0; 1] folgende Wahrscheinlichkeitstabelle:

y	0	1	2	3	4	5
P(Y = y)	a	0,40	0,25	a + b	b	0,05

5.1

Bestimmen Sie  a  und  b,  wenn  P(Y ≤ 2) = 0,70  ist.
(Ergebnis:  a = 0,05;  b = 0,10)   (3 BE)

5.2

Errechnen Sie, wie viele Stunden Herr Molle im Beobachtungszeitraum durchschnittlich zu spät nach Hause kommt.
(Ergebnis:  E(Y) = 2)   (2 BE)

5.3

Berechnen Sie die Wahrscheinlichkeit  P(|Y – E(Y)| ≤ 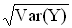).   (4 BE)