1.0   

Die Post eines kleineren Landes gibt den Druck einer neuen Sonderbriefmarke in Auftrag. Beim ersten Probedruck einer größeren Menge dieser Marken werden noch Fehler bei der Zähnung, beim Farbton sowie bei der Grafik festgestellt. Es kann davon ausgegangen werden, dass diese Fehlerarten unabhängig voneinander auftreten und dass die Wahrscheinlichkeiten ihres Auftretens während des Probedrucks konstant bleiben.
Folgende Bezeichnungen seien vorgegeben:
Z:  Bei einer zufällig ausgewählten Marke ist die Zähnung in Ordnung. 
F:  Bei einer zufällig ausgewählten Marke ist die Farbe in Ordnung. 
G:  Bei einer zufällig ausgewählten Marke ist die Grafik in Ordnung.
Die Wahrscheinlichkeit für einen Farbfehler beträgt P(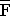) = 0,3,
diejenige für einen Fehler bei der Zähnung P(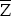) = 0,5.

1.1

Eine zufällig ausgewählte Briefmarke wird hinsichtlich der Merkmale Z, F und G untersucht.
Veranschaulichen Sie alle möglichen Ergebnisse dieser Untersuchung mit Hilfe eines Baumdiagramms. Begründen Sie, dass die Wahrscheinlichkeit für einen Fehler in der Grafik 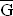P() = 0,2 beträgt, wenn bekannt ist, dass eine fehlerfreie Briefmarke mit der Wahrscheinlichkeit P(ZFG) = 0,28 auftritt. Bestimmen Sie anschließend die Wahrscheinlichkeiten aller acht Elementarereignisse.   (8 BE)

1.2

Nun werden folgende Ereignisse betrachtet:

E1:	"Eine zufällig ausgewählte Marke hat mindestens zwei Fehler oder einen Zähnungsfehler."
E2:	"Eine zufällig ausgewählte Marke hat genau einen Fehler."

Überprüfen Sie rechnerisch, ob die Ereignisse E₁ und E₂ stochastisch unabhängig sind.   (5 BE)

2.0

Die Druckmaschine wird korrigiert. Die Zufallsgröße  X  gibt die Anzahl der Fehlerarten an, die  bei einer zufällig ausgewählten Briefmarke des neuen Drucks auftreten. Die Wahrscheinlichkeitsverteilung der Zufallsgröße  X  kann mit Hilfe eines geeigneten Parameters  a IR  so dargestellt werden:

2.1

Berechnen Sie den Parameter  a.   (4 BE)

Für die Teilaufgaben  2.2  bis  2.4  gilt:  a = 2.

2.2

Berechnen Sie die Wahrscheinlichkeit dafür, dass der Wert der Zufallsgröße innerhalb der zweifachen Standardabweichung um den Erwartungswert liegt.   (4 BE)

2.3

Bestimmen Sie die Wahrscheinlichkeit dafür, dass von 200 zufällig ausgewählten Briefmarken des neuen Drucks mindestens 150 und höchstens 170 fehlerfrei sind.   (2 BE)

2.4

Geben Sie die Wertetabelle der zugehörigen kumulativen Verteilungsfunktion  F  an und zeichnen Sie deren Graph farbig in ein geeignetes Koordinatensystem.
Bestimmen Sie ferner den Wert k = 1 – F(2,3) und interpretieren Sie ihn im Sinne der vorliegenden Thematik.   (4 BE)

3.0

Durch weitere Verbesserungen an der Druckmaschine ist es gelungen, die Anzahl der fehlerhaften Briefmarken weiter zu verringern. Bei den nachfolgenden Untersuchungen kann aufgrund der großen Stückzahlen davon ausgegangen werden, dass die Anzahl der fehlerhaften Briefmarken einer Druckreihe binomialverteilt ist.
Bei einer Druckreihe von  90 000  Sondermarken wird eine Standardabweichung von  σ = 90  festgestellt.

3.1

Berechnen Sie, für welche Werte der Wahrscheinlichkeit  p  eine zufällig herausgegriffene Marke dieser Druckreihe fehlerhaft ist. Welcher dieser Werte trifft zu, wenn insgesamt mehr fehlerfreie als fehlerhafte Briefmarken gedruckt werden?   (5 BE)
(Mögliches Zwischenergebnis:  100p² – 100p + 9 = 0 )

3.2

Mit wie vielen fehlerhaften Marken ist in dieser Druckreihe zu rechnen, wenn die Wahrscheinlichkeit für einen Fehler 0,1 beträgt?   (2 BE)

4.

Vor Beginn des endgültigen Drucks behauptet die Post gegenüber der Druckerei, dass der Anteil fehlerhafter Briefmarken immer noch mehr als  5%  beträgt (Gegenhypothese). Eine Prüfkommission führt daher einen Signifikanztest mit 200 zufällig ausgewählten Briefmarken des letzten großen Druckes durch.
Geben Sie die Testgröße, die Art des Tests sowie die Nullhypothese an und ermitteln Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem 1%-Niveau.   (6 BE)

1.0

Für eine Marktanalyse werden 2000 zufällig ausgewählte Bankkunden (beiderlei Geschlechts) danach befragt, ob sie beim Kauf von Wertpapieren eher risikofreudig (r) oder konservativ (k) handeln.
Die Befragten sind – wie folgt – drei Altersgruppen zuzuordnen:
690 Personen zählen zu den jungen Anlegern (J), 780 zur Gruppe mittleren Alters (M) und 530 zu den Senioren (S).
800 der Kunden sind eher konservative Anleger; davon sind 320 Senioren.
(Die folgenden drei Teilaufgaben beziehen sich ausschließlich auf die oben erwähnten 2000 Bankkunden!)

1.1

Die Analyse zeigt außerdem, dass die Anzahl der konservativen Anleger bei den Personen mittleren Alters dreimal so hoch ist wie bei den jungen Kunden. Ermitteln Sie auf Grund aller bisherigen Angaben die Anzahl der jungen konservativen Anleger.   (Ergebnis: 120)   (4 BE)

1.2

Berechnen Sie nun die Wahrscheinlichkeit, mit der es sich bei einer zufällig ausgewählten Person um einen jungen, eher risikofreudigen Bankkunden handelt.   (3 BE)

1.3

Untersuchen Sie, ob die Zugehörigkeit zur Gruppe der Senioren stochastisch unabhängig ist von der Zugehörigkeit zur Gruppe der konservativen Anleger.   (4 BE)

2.0

Anleger Muck sitzt an seinem PC, um am Online-Broking teilzunehmen. Seine fünfstellige Kennnummer enthält die Ziffern 2, 3, 4, 7 und 8.

2.1

Wie viele verschiedene Kennnummern können aus diesen Ziffern gebildet werden, wenn jede der Ziffern genau einmal vorkommen darf?   (2 BE)

2.2

Ein „Hacker“ versucht, die ihm unbekannte 5-stellige Kennnummer von Herrn Muck durch unsystematisches Probieren herauszufinden. Ihm ist bekannt, dass die erste Ziffer der gesuchten Kennnummer die  3  ist, die übrigen Ziffern kennt er jedoch nicht. Mit welcher Wahrscheinlichkeit „errät“ der Hacker die Kennnummer bereits beim 1. Versuch?   (3 BE)

3.0

Ein großes Internetcafé hat Plätze an 50 PCs. Umfangreiche Untersuchungen haben gezeigt, dass die Wahrscheinlichkeit dafür, dass ein PC in der Kernzeit belegt ist, für jeden der 50 PCs  p = 0,7  beträgt.
(In den beiden folgenden Aufgaben wird nur dieser Zeitbereich betrachtet.)

3.1

Berechnen Sie, mit welcher Wahrscheinlichkeit die Anzahl der belegten PCs innerhalb der einfachen Standardabweichung um den Erwartungswert liegt.   (5 BE)

3.2

Berechnen Sie die Wahrscheinlichkeit dafür, dass zu einem bestimmten Zeitpunkt mindestens 15 PCs frei sind.   (2 BE)

4.0

Der Internetprovider  A  behauptet in Werbeanzeigen, dass er einen Marktanteil von 60% besitzt. Konkurrent  B  hält diesen Wert für zu hoch (Gegenhypothese) und veranlasst daher die Durchführung eines Hypothesentests auf 5%-Niveau, mit dem die Aussage von  A  überprüft werden soll. Dazu werden 200 Internetnutzer befragt.

4.1

Geben Sie die Art des Tests und die Testgröße an und ermitteln Sie den größtmöglichen Ablehnungsbereich der Nullhypothese.
Worin besteht bei diesem Test der Fehler 2. Art?   (7 BE)

4.2

Zeigen Sie anhand eines Beispiels für den möglichen Ausgang der Stichprobe, wie die Entscheidungsregel anzuwenden ist.   (2 BE)

5.0

Ein Börseninformationsdienst bietet ein Abonnement an. Abonnenten nehmen automatisch an einem Preisausschreiben teil, bei dem es  1-mal  10000 €, 10-mal  500 €  und  100-mal  20 €  zu gewinnen gibt. Die Anzahl der Teilnehmer ist  n, wobei  n IN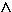    n ≥ 111.

5.1

Die Zufallsgröße  X  gibt den von einem zufällig ausgewählten Teilnehmer erzielten Gewinn bei obigem Preisausschreiben an.
Ermitteln Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße  X  und den Erwartungswert  E(X)  in Abhängigkeit von  n.   (5 BE)
(Teilergebnis: P(X = 0)  =  )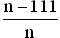

5.2

Berechnen Sie nun, wie groß die Teilnehmerzahl  n  mindestens sein müsste, damit ein zufällig ausgewählter Abonnent mit einer Wahrscheinlichkeit von mehr als 90% keinen Gewinn erzielt.   (3 BE)