Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 2003

Aufgabengruppe S:   S I   S II

S I

1.0       

In einem Mischwald wird eine Versuchsfläche auf Schäden durch Wildverbiss an den Jungtrieben der Bäume untersucht. Einzige Nadelbaumart ist die Fichte (F); sie macht 25 % des Baumbestandes aus. Auf der Versuchsfläche befinden sich außerdem 45 % Buchen (B), ansonsten Eichen (E). Alle Baumarten kommen auf der Fläche gleichmäßig verteilt vor.
Bei einer Zählung werden folgende Schadensanteile durch Verbiss unter den jeweiligen Baumarten beobachtet: 20 % bei Fichten, 30 % bei Buchen und 25 % bei Eichen.
Als Zufallsexperiment wird die Auswahl eines beliebigen Baumes betrachtet; dabei wird die Baumart festgestellt und geprüft, ob Verbiss (V) vorliegt oder nicht (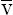). Die gegebenen Prozentsätze werden als Wahrscheinlichkeiten interpretiert.

1.1

Ermitteln Sie alle  6 Elementarereignisse und deren Wahrscheinlichkeiten mit Hilfe eines Baumdiagramms.   (6 BE)

1.2.0

Es werden nun folgende Ereignisse betrachtet:
A₁: „Ein zufällig ausgewählter Baum ist ein Laubbaum ohne Verbiss.“
A₂: „Ein zufällig ausgewählter Baum ist eine Fichte oder eine Eiche.“

1.2.1

Geben Sie diese Ereignisse in aufzählender Mengenschreibweise an.   (2 BE)

1.2.2

Prüfen Sie, ob die beiden Ereignisse  A₁  und  A₂  stochastisch unabhängig sind.   (4 BE)

1.3.0

Nun werden innerhalb der Versuchsfläche 20 Bäume zufällig ausgewählt.

1.3.1

Ermitteln Sie die Wahrscheinlichkeit dafür, dass sich unter diesen mehr als fünf Fichten befinden.   (3 BE)

1.3.2

Berechnen Sie die Wahrscheinlichkeit dafür, dass die Zahl der Laubbäume höchstens um  2  vom Erwartungswert abweicht.   (4 BE)

1.4.0

Bei einer Waldbegehung wird vermutet, dass sich der Schadensanteil bei Fichten (siehe 1.0) vergrößert hat (Gegenhypothese). Um dies zu überprüfen, werden 200 zufällig ausgewählte Fichten auf Wildverbiss untersucht. Sind hiervon mehr als 50 geschädigt, wird diese Vermutung als bestätigt angesehen.

1.4.1

Geben Sie die Testgröße T, die Nullhypothese H₀ und den Ablehnungsbereich der Nullhypothese an. Bestimmen Sie, mit welcher Wahrscheinlichkeit man sich irrtümlich für eine Vergrößerung des Schadensanteils entscheidet.   (6 BE)

1.4.2

Beschreiben Sie, worin bei diesem Beispiel der Fehler 2. Art besteht.   (2 BE)

2.0

Bei der Untersuchung von Kiefernnadeln wird die Länge L von 200 zufällig ausgewählten Nadeln bestimmt und in sechs Längengruppen eingeteilt. Die Zufallsgröße  X  gibt die Nummer der jeweiligen Längengruppe an. Dabei ergibt sich folgende Verteilung mit  a, b IN:

Die Wahrscheinlichkeit, dass eine zufällig ausgewählte Nadel in einer der Längengruppen  4  bis  6  liegt, beträgt dabei  0,66.

2.1

Berechnen Sie die Werte der Parameter  a  und  b.    (3 BE)

2.2.0

Setzen Sie für die folgenden Teilaufgaben  a = 20  und  b = 30.

2.2.1

Erstellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße  X  und zeichnen Sie ein zugehöriges Histogramm.   (4 BE)

2.2.2

Bestimmen Sie, mit welcher Wahrscheinlichkeit die Zufallswerte innerhalb der einfachen Standardabweichung um den Erwartungswert liegen.   (6 BE)

S II

Ein Hersteller von Kopierern bietet ein bestimmtes Gerät in zwei verschiedenen Qualitäten an: in einer hochwertigen (H) und in einer einfachen (E). Ein Gerät des Typs E liefert im Schnitt weniger gute Kopien als ein Gerät des Typs H.

1.0

Die Testabteilung der Firma hat in einer Versuchsreihe herausgefunden, dass unter gleichen Bedingungen beim Typ H im Schnitt 45 von 50 Kopien einwandfrei sind; beim Typ E sind im Schnitt 20 % der Kopien fehlerhaft.

1.1

Bestimmnen Sie jeweils auf 3 Nachkommastellen gerundet die Wahrscheinlichkeiten dafür, dass ein Gerät des Typs H bei einer Serie von 50 Kopien
a) mehr als 40 einwandfreie Kopien liefert.
b) am Anfang 49 gute, dann 1 fehlerhafte Kopie liefert.   (5 BE)

1.2

Berechnen Sie, mit welcher Wahrscheinlichkeit die Anzahl der guten Kopien für ein Gerät E bei einer Serie von 50 Kopien innerhalb der einfachen Standardabweichung um den zugehörigen Erwartungswert liegt.   (6 BE)

2.0

Ein Käufer hat ein Gerät des Typs H erworben. Er kennt die Untersuchungsergebnisse des Herstellers. Nach einem halben Jahr regelmäßiger Benutzung vermutet der Käufer jedoch, dass eine erkennbare Verschlechterung der Kopierqualität eingetreten sei (Gegenhypothese). Er führt einen Test durch und macht 50 Kopien von einer bestimmten Originalseite. Erhält er dabei mehr als 42 einwandfreie Kopien, so will er von seiner Meinung wieder abrücken.

2.1

Geben Sie die Testgröße sowie die Art des Tests an. Formulieren Sie in Worten die Nullhypothese H₀ und geben Sie die zugehörige Wahrscheinlichkeit sowie den maximalen Ablehnungsbereich von H₀ an.   (4 BE)

2.2

Bestimmen Sie die Wahrscheinlichkeit des Fehlers 1. Art und erläutern Sie die beiden Möglichkeiten den Test abzuändern, wenn man die Wahrscheinlichkeit für den Fehler 1. Art verringern möchte.   (4 BE)

2.3

Der misstrauische Käufer ändert sein Testverfahren ab. Zwar belässt er es bei 50 Kopien, doch soll der Fehler 1. Art mit einer Wahrscheinlichkeit von höchstens 2 % eintreten. Berechnen Sie für diesen Fall den maximalen Ablehnungsbereich.   (3 BE)

3.0

Die Geräte des Typs H und E sind äußerlich nur an Hand eines Aufklebers zu unterscheiden. Wegen einer Modellumstellung soll das Lager des Herstellers in Bezug auf oben erwähnten Gerätetyp geräumt werden. Der sehr große Restbestand an Kopierern der Typen H und E enthält genau 40 % einfache Geräte E. Von allen Geräten werden die Aufkleber entfernt. Je vier zufällig ausgewählte Geräte werden als Paket verpackt und Händlern in einer Sonderaktion zu einem sehr niedrigen Preis angeboten.
Die Zufallsgröße  X  gibt die Anzahl der Geräte vom Typ E in einem solchen „Viererpaket“ an.

3.1

Erstellen Sie eine Wertetabelle der Wahrscheinlichkeitsverteilung der Zufallsgröße  X  (4 Nachkommastellen)  und zeichnen Sie ein dazugehöriges Histogramm.   (4 BE)

3.2

Geben Sie für die zur Zufallsgröße  X  gehörige kumulative Verteilungsfunktion  F  eine Wertetabelle an und zeichnen Sie den Graphen von  F.   (4 BE)

3.3

Ermitteln Sie die Wahrscheinlichkeit dafür, dass in einem solchen „Viererpaket“ mindestens zwei und höchstens drei Geräte des Typs E zu finden sind.   (2 BE)

4.0

Ein Händler hat 50 Pakete aus der Sonderaktion des Herstellers erworben. Er erwägt, alle 200 erworbenen Geräte auf ihre Qualität hin zu überprüfen, um die Geräte des Typs H herauszufinden. Für Typ H könnte er dann pro Stück 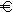80 mehr verlangen als für Typ E.

4.1

Ermitteln Sie zunächst, wie viele Geräte des Typs H der Händler haben müsste, um Mehreinnahmen von mindestens 8000 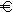zu erzielen. Berechnen Sie dann die Wahrscheinlichkeit dafür, dass er dieses Ziel erreicht, wenn man davon ausgeht, dass alle Geräte verkauft werden. Beachten Sie die Angaben in  3.0  über den Anteil der Geräte eines Typs.   (4 BE)

4.2

Untersuchen Sie, ob der Händler auch dann noch Mehreinnahmen erwarten könnte, wenn man berücksichtigt, dass ihm durch das Prüfverfahren pro Gerät zusätzliche Kosten in Höhe von 40 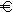entstehen.   (4 BE)