| 1.0 |
Ein Erlebnisparkbetreiber befragt eine große Zahl von Besuchern, ob sie aus der Region (R) kommen oder überregionale Besucher 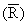 sind. Ferner interessiert, ob sie mit dem Auto(A), dem Bus(B) oder auf sonstige Weise(S) angereist sind. 45% der Befragten kommen aus der Region; von diesen haben 68% das Auto und 28% den Bus benutzt. 62% der überregionalen Besucher sind mit dem Auto angereist, 36% mit dem Bus. sind. Ferner interessiert, ob sie mit dem Auto(A), dem Bus(B) oder auf sonstige Weise(S) angereist sind. 45% der Befragten kommen aus der Region; von diesen haben 68% das Auto und 28% den Bus benutzt. 62% der überregionalen Besucher sind mit dem Auto angereist, 36% mit dem Bus.
Das Ergebnis der Befragung wird als Zufallsexperiment aufgefasst, die gegebenen Prozentsätze als Wahrscheinlichkeiten interpretiert. |
| |
|
| 1.1 |
Ermitteln Sie alle 6 Elementarereignisse des Zufallsexperiments und deren Wahrscheinlichkeiten mit Hilfe eines Baumdiagramms. (6BE) |
| |
|
| 1.2 |
Es werden nun folgende Ereignisse betrachtet:
E1: " Ein Besucher kommt nicht aus der Region oder reist mit dem Bus an."
E2: " Ein Besucher stammt aus der Region und reist nicht mit dem Auto an."
Geben Sie diese Ereignisse in aufzählender Mengenschreibweise an. (2BE) |
| |
|
| 2.0 |
An der Kasse des Erlebnisparks werden Bargeld und Kreditkarten akzeptiert. Die Wahrscheinlichkeit, dass ein Besucher mit Bargeld bezahlt, beträgt p. Es werden im Folgenden 12 zufällig ausgewählte Personen betrachtet. |
| |
|
| 2.1 |
Berechnen Sie für den Fall p= 0,8 die Wahrscheinlichkeit, dass von diesen 12 Personen mindestens 11 mit Bargeld bezahlen. (3BE) |
| |
|
| 2.2 |
Ermitteln Sie wie groß p mindestens sein müsste, damit mit einer Wahrscheinlichkeit von wenigstens 0,5 alle 12 Personen mit Bargeld bezahlen. (3BE) |
| |
|
| 3.0 |
Nach Angaben der Betreiber des Erlebnisparks gehen 75% der Besucher ins Varieté(V), 65% fahren mit der Wildwasserbahn(W), während 5% keines dieser beiden Angebote nutzen. Alle Prozentangaben werden als Wahrscheinlichkeiten interpretiert. |
| |
|
| |
|
| 3.1 |
Beschreiben Sie die Ereignisse 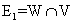 und und 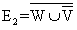 möglichst einfach mit Worten im Sinne der vorliegenden Thematik. Berechnen sie deren Wahrscheinlichkeiten z.B. mit Hilfe einer Vierfeldertafel. (6BE) möglichst einfach mit Worten im Sinne der vorliegenden Thematik. Berechnen sie deren Wahrscheinlichkeiten z.B. mit Hilfe einer Vierfeldertafel. (6BE) |
| |
|
| 3.2 |
Untersuchen Sie durch Rechnung, ob die Ereignisse W und V stochastisch unabhängig sind. (2BE) |
| |
|
| 4 |
Ein Achterbahnzug besitzt 40 Sitzplätze. Am Wochenende ist ein Sitzplatz mit der Wahrscheinlichkeit 0,9 besetzt. Die Zufallsgröße X gibt die Anzahl der freien Plätze bei einer zufällig ausgewählten Fahrt an.
Untersuchen Sie, ob der Wert x=6 der Zufallsgröße X innerhalb der doppelten Standardabweichung um den Erwartungswert liegt. (6BE) |
| |
|
| 5.0 |
Bei entsprechenden, vom Zufall abhängigen Voraussetzungen wird die Öffnungszeit des Parks verlängert. Die Zufallsgröße Y gibt die Verlängerung der Öffnungszeit in Stunden an. Die Wahrscheinlichkeitsverteilung lässt sich mit Hilfe eines Parameters a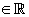 so darstellen: so darstellen:
| y | 0 | 1 | 1,5 | 2 |
| P(Y=y) | 0,4 | 1,5a | a | 0,5a |
|
| |
|
| 5.1 |
Berechnen Sie den Parameterwert a und stellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße Y geeignet graphisch dar. (3BE) |
| |
|
| 5.2 |
Setzen Sie a=0,2. Ermitteln Sie die Wahrscheinlichkeit dafür, dass die Verlängerung der Öffnungszeit größer ist als der Erwartungswert E(Y). (3BE) |
| |
|
| 6 |
Auf vielfache Nachfrage bietet das Parkrestaurant mehr fleischlose Gerichte an als früher. Durch einen Test soll herausgefunden werden, ob sich dadurch der Anteil der verkauften fleischlosen Gerichte gegenüber bisher 30% erhöht hat (Gegenhypothese). Hierzu werden die Essensbestellungen von 200 zufällig ausgewählten Gästen ausgewertet.
Geben Sie die Testgröße T und die Nullhypothese H0 an. Bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem 5%-Niveau.
Entscheiden Sie aufgrund dieses Tests ob die Nullhypothese abgelehnt wird, wenn 71 fleischlose Gerichte bestellt werden. (6BE) |

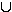 S möglichst einfach mit Worten im Sinne der vorliegenden Thematik und berechnen Sie seine Wahrscheinlichkeit. (3 BE)
S möglichst einfach mit Worten im Sinne der vorliegenden Thematik und berechnen Sie seine Wahrscheinlichkeit. (3 BE)