| 1. |
Am 22.04.2005 wurden 812.000 Tickets zur FIFA WM 2006 verlost. 900.000 Menschen hatten zuvor insgesamt 8,1 Millionen Karten bestellt. Jede Kartenbestellung hat die gleiche Chance.Ein Fußballfan hat 16 Karten bestellt. Berechnen Sie jeweils die Wahrscheinlichkeit dafür, dass er
a) keine Karte
b) mindestens eine Karte
c) genau zwei Karten
d) nur jeweils genau eine Karte (dabei kann wie oben p= 0,1 angenommen werden) für das
Eröffnungsspiel und das Finale erhält.
|
(6BE)
|

|
| 2.0 |
Eine Fangruppe hat es geschafft, 20 Karten für das Eröffnungsspiel zu erhalten. Die Plätze sind in drei Blöcken A, B und C verteilt. Im Block A erhält die Gruppe neun, in B sechs und in C fünf Karten. Die 20 Karten werden zufällig auf die 20 Fans verteilt.
Rosi erhält als erste und Sven als zweiter der Fangruppe die Eintrittskarte.
Die Verteilung von Rosi und Sven auf die einzelnen Blöcke wird als Zufallsexperiment aufgefasst.
|
|
|
| 2.1 |
Bestimmen Sie mit Hilfe eines Baumdiagramm die Wahrscheinlichkeiten aller 9 Elementarereignisse.
|
(6BE) |
 |
| 2.2 |
Berechnen Sie die Wahrscheinlichkeit dafür, dass Rosi und Sven Karten für denselben Block erhalten.
|
(2BE)
|

|
| 3.0 |
Um gefährliche Gegenstände (G) aufzuspüren, müssen die Zuschauer eine Sicherheitsschleuse passieren.
Erfahrungsgemäß wird bei 1% aller Personen ein Alarm (A) ausgelöst. In 2 von 1000 Fällen führt eine Person einen gefährlichen Gegenstand mit und löst den Alarm aus. Allerdings kann 1 von 1000 Personen mit einem gefährlichen Gegenstand die Schleuse passieren, ohne Alarm auszulösen.
|
|
|
| 3.1 |
Ermitteln Sie mit Hilfe einer Vierfeldertafel die Wahrscheinlichkeiten folgender Ereignisse:
E1: "| Bei einer zufällig ausgewählten Person wird Alarm ausgelöst, obwohl sie keinen gefährlichen Gegenstand mit sich führt." |
E2: "Eine zufällig ausgewählte Person führt keinen gefährlichen Gegenstand mit sich."
|
(5BE)
|

|
| 3.2 |
Untersuchen Sie durch Rechnung, ob die Ereignisse A und G stochastisch unabhängig sind.
|
(2BE)
|

|
| 3.3 |
Berechnen Sie P(A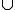 G). G).
|
(2BE)
|

|
| 3.4.0 |
Die Wahrscheinlichkeit, dass eine Person einen Alarm auslöst, beträgt 0,01. Im Folgenden wird eine zufällig ausgewählte Gruppe von 200 Personen betrachtet, die die Schleuse passieren. Die Zufallsgröße X gibt an, wie oft bei dieser Gruppe Alarm ausgelöst wird.
|
|
|
| 3.4.1 |
Berechnen Sie die Wahrscheinlichkeit dafür, dass mehr als fünfmal Alarm ausgelöst wird. |
(3BE) |

|
| 3.4.2 |
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Zahl der ausgelösten Alarme innerhalb der einfachen Standardabweichung um den Erwartungswert liegt. |
(5BE) |
 |
| 4.0 |
Der Torwart der Mannschaft A kann von 10 Elfmetern durchschnittlich 3 abwehren.
|
|
|
| 4.1 |
Es gibt 8 Elfmeter auf das Tor der Mannschaft A. Berechnen Sie die Wahrscheinlichkeit dafür, dass dabei höchstens 3 Tore fallen.
|
(3BE)
|

|
| 4.2 |
Der Ersatztorwart behauptet, dass er mehr Elfmeterschüsse abwehren kann (Gegenhypothese). Der Trainer beschließt einen Test mit dem Ersatztorwart bei 100 Elfmeterschüssen.
Geben Sie die Testgröße sowie die Nullhypothese an und berechnen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem 5%- Niveau.
Welche Trainerentscheidung legt der Test nahe, wenn der Ersatztorwart 35 Elfmeter abwehren kann? |
(6BE) |
 |
|

zu den Lösungen
Druckversion
|
