1.0
An einer Fachoberschule werden nur die Fachrichtungen Sozialwesen (S), Technik (T) und Wirtschaft (W) angeboten. An der Schule werden 275 Mädchen (M) und 225 Jungen (J) unterrichtet. 170 Schüler haben die Fachrichtung S gewählt, davon 143 Mädchen. Für die Fachrichtung T haben sich 22 Mädchen und 108 Jungen entschieden. Bei einem Zufallsexperiment werden bei einem zufällig herausgegriffenen Schüler Geschlecht und Fachrichtung notiert. Relative Häufigkeiten werden dabei als Wahrscheinlichkeiten interpretiert.
1.1
Erfassen Sie zunächst die Schülerzahlen in einer Tabelle nach folgendem Muster und ermitteln Sie alle Elementarereignisse und deren Wahrscheinlichkeiten.
| S | T | W | Σ | |
| M | ||||
| J | ||||
| Σ |
(6 BE)
1.2.0
Es werden nun folgende Ereignisse betrachtet:
E1: "Die zufällig ausgewählte Person ist ein Junge."
E2: "Die zufällig ausgewählte Person hat den W-Zweig gewählt."
1.2.1
Untersuchen Sie, ob die Ereignisse E1 und E2 stochastisch unabhängig sind.
Interpretieren Sie das Ergebnis im vorgegebenen Sachzusammenhang.
(4 BE)
1.2.2
Berechnen Sie die Wahrscheinlichkeit 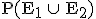 .
.
(2 BE)
2.0
Der Mathematiklehrer einer größeren Klasse hat durch Beobachtungen über einen längeren Zeitraum bemerkt, dass ab und zu einige Schüler ihre Hausaufgabe zum fälligen Termin nicht gemacht haben. Die Zufallsgröße X gibt die Anzahl der Schüler dieser Klasse an, die zu einem beliebigen Termin die Mathematik-Hausaufgabe nicht erledigt haben. Dabei ergibt sich mit den Parametern a, b, c 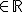 folgende Verteilung (andere Zufallswerte treten nicht auf):
folgende Verteilung (andere Zufallswerte treten nicht auf):
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P(X = x) | a | b | 0,2 | b + c | c | 0,1 | 0,05 |
2.1
Berechnen Sie die Parameter a, b und c, wenn im Durchschnitt 3 Schüler ihre Hausaufgabe nicht gemacht haben und P(X ≤ 3) = 0,65 ist. Stellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße X geeignet graphisch dar.
[ Teilergebnis: a = 0,05; b = 0,1 ]
(8 BE)
2.2
Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Zufallswerte innerhalb der einfachen Standardabweichung um den Erwartungswert liegen.
(4 BE)
3.0
Bei einem Multiple-Choice-Test werden einem Prüfling vier unabhängig voneinander zu beantwortende Fragen vorgelegt, die er alle zu bearbeiten hat. Der Prüfling hat sich auf die Prüfung schlecht vorbereitet und muss sich daher bei allen Fragen auf reines Raten verlassen.
3.1
Zu jeder der vier Fragen gibt es drei mögliche Antworten, von denen genau eine richtig ist. Der Test ist bestanden, wenn der Prüfling mindestens zwei aufeinanderfolgende Fragen richtig beantwortet hat. Berechnen Sie die Wahrscheinlichkeit dafür, dass der Prüfling den Test besteht.
(4 BE)
3.2
Der Test wird nun abgeändert. Alle 4 Fragen müssen jetzt richtig beantwortet werden, um zu bestehen. Berechnen Sie, wie viele "Antworten" zu jeder Frage mindestens gegeben sein müssen, damit der Prüfling den Test mit einer Wahrscheinlichkeit von höchstens 0,01 besteht.
(4 BE)
4.0
Im Kunstunterricht wird den Schülern ein zeitgenössisches Gemälde gezeigt, zu dem sie unabhängig voneinander ihre Meinung äußern sollen. Aus Erfahrung weiß der Lehrer, dass die Schüler sich im Schnitt zu 85% positiv, zu 11% negativ äußern; 4% sind neutral.
4.1
Bestimmen Sie die Wahrscheinlichkeiten dafür, dass von 10 Schülern
a) sich alle positiv äußern,
b) höchstens einer sich negativ äußert.
(3 BE)
4.2
Es tritt die Vermutung auf, dass der Anteil der Schüler, die das Gemälde nicht positiv beurteilen, in letzter Zeit gestiegen ist (Gegenhypothese). Daher führt der Lehrer einen Test durch, bei dem er 100 Schülerantworten auswertet. Geben Sie zu diesem Test die Testgröße sowie die Nullhypothese an und ermitteln Sie deren größtmöglichen Ablehnungsbereich, wenn das Signifikanzniveau 2% betragen soll.
(5 BE)

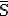 )
und 3% der Schränke haben Glastüren mit defekten Scharnieren. Aus allen
Schränken des Möbellagers wird nun ein Schrank zufällig ausgewählt.
)
und 3% der Schränke haben Glastüren mit defekten Scharnieren. Aus allen
Schränken des Möbellagers wird nun ein Schrank zufällig ausgewählt.