Prüfung zur Erlangung der Fachhochschulreife
Frühjahr 1999

Aufgabengruppe S:   S I   S II

S I

Eine Urne enthält sechs rote und vier weiße Kugeln, die sich nur durch ihre Farbe unterscheiden. Außerhalb der Urne stehen noch genügend viele rote und weiße Kugeln als zusätzlicher Kugelvorrat zur Verfügung.
Ein Zufallsexperiment besteht darin, dass nacheinander drei Kugeln zufällig aus der Urne gezogen werden, wobei nach jeder entnommenen Kugel eine andersfarbige Kugel aus dem Kugelvorrat wieder in die Urne gelegt wird.

1.       

Zeichnen Sie zu dem beschriebenen Zufallsexperiment ein Baumdiagramm und berechnen Sie die Wahrscheinlichkeiten aller Elementarereignisse.   (6 BE)
(Teilergebnis: P({RRR}) = 0,120; P({WWW}) = 0,024)

2.0

Es werden nun folgende Ereignisse betrachtet:
A: "Es werden ausschließlich gleichfarbige Kugeln gezogen."
B: "Unter den drei gezogenen Kugeln befinden sich mindestens zwei rote Kugeln."

2.1

Berechnen Sie die Wahrscheinlichkeiten P(A) und P(B). Untersuchen Sie auch, ob die Ereignisse A und B stochastisch unabhängig sind.   (5 BE)

2.2

Drücken Sie das Ereignis 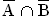möglichst einfach mit Worten aus und berechnen Sie dessen Wahrscheinlichkeit.   (3 BE)

2.3

Nun wird das Zufallsexperiment unter stets gleichen Anfangsbedingungen zehnmal durchgeführt. Berechnen Sie jeweils die Wahrscheinlichkeit, dass das Ereignis A
a) genau dreimal,
b) nur bei den ersten drei Malen,
c) höchstens einmal eintritt.   (5 BE)

3.0

Die Zufallsgröße  X  gibt die Anzahl der roten Kugeln unter den drei gezogenen Kugeln an.

3.1

Stellen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße  X  in Tabellenform dar.   (2 BE)

3.2

Zeichnen Sie mit Hilfe einer Wertetabelle den Graphen der kumulativen Verteilungsfunktion der Zufallsgröße  X.   (4 BE)

4.0

Für die Werte der Zufallsgröße  X  aus Aufgabe 3  wird bei einem Spiel folgender Gewinn/Verlust-Plan zugrunde gelegt:

4.1

Berechnen Sie, wie hoch der Auszahlungsbetrag  a  angesetzt werden müsste, damit es sich um ein faires Spiel handelt.   (4 BE)

4.2

Die Wahrscheinlichkeit, bei diesem Spiel einen Geldbetrag zu gewinnen, beträgt exakt  p = 0,352. Es werden zehn Spiele unter stets gleichen Anfangsbedingungen durchgeführt.
Untersuchen Sie, ob es günstiger ist, auf das Ereignis  E: "Es werden zwei oder drei Spiele gewonnen" oder auf das Ereignis 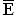zu setzen.   (4 BE)

5.

Bei einem anderen Spiel geht man davon aus, dass die Gewinnwahrscheinlichkeit  p = 0,45  beträgt (Nullhypothese). Im Rahmen eines zweiseitigen Signifikanztests wird das Spiel 100-mal durchgeführt. Geben Sie die Gegenhypothese an und bestimmen Sie den größtmöglichen Ablehnungsbereich der Nullhypothese auf dem  1%-Signifikanzniveau.
Wie ist bei obigem Test mit der Nullhypothese zu verfahren, wenn sich bei dessen Durchführung 32 Gewinnspiele ergeben?   (7 BE)

S II

1.0

In einem Kindergarten trinkt jedes der Kinder in der Frühstückspause genau eines der Getränke Kakao, Erdbeermilch bzw. Vanillemilch jeweils mit der Wahrscheinlichkeit  P({K}) = 0,6 , P({E}) = 0,25  bzw.  P({V}) = 0,15.  Nehmen Sie an, dass diese Wahrscheinlichkeiten konstant sind und dass die Entscheidungen für jedes der drei Getränke jeweils unabhängig erfolgen.

1.1

Veranschaulichen Sie das Wahlverhalten eines zufällig ausgewählten Kindes an zwei aufeinanderfolgenden Tagen in einem Baumdiagramm. Ermitteln Sie auch die Wahrscheinlichkeiten sämtlicher Elementarereignisse.   (5 BE)

1.2

Berechnen Sie jeweils, mit welcher Wahrscheinlichkeit ein zufällig ausgewähltes Kind an fünf aufeinanderfolgenden Tagen
a) stets Kakao,
b) viermal Kakao und einmal Erdbeermilch,
c) niemals Vanillemilch wählt.   (6 BE)

2.0

Nun wird eine Gruppe von 20 Kindern zufällig ausgewählt. Die Zufallsgröße  X  gibt die Anzahl der Kinder dieser Gruppe an, die für diesen Tag Vanillemilch bestellt haben.

2.1

Begründen Sie, dass die Zufallsgröße  X  binomial verteilt ist und bestimmen Sie die Wahrscheinlichkeit  P(X ≤ 1).   (3 BE)

2.2

Ermitteln Sie, mit welcher Wahrscheinlichkeit mindestens zwei der 20 Kinder Vanillemilch wählen.   (2 BE)

3.0

60 % der Kinder des Kindergartens sind Mädchen. Betrachtet werden die beiden Ereignisse
E₁: "Ein zufällig ausgewähltes Kind ist ein Mädchen."
E₂: "Ein zufällig ausgewähltes Kind wählt Erdbeermilch."
Es sei ferner bekannt, dass P(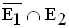) = 0,10 gilt.

3.1

Zeigen Sie rechnerisch, dass die beiden Ereignisse vereinbar sowie stochastisch unabhängig sind.   (6 BE)

3.2

Berechnen Sie die folgenden Wahrscheinlichkeiten:
a) P(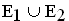);       b) 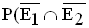).   (4 BE)

4.0

Bei einem Kindergartenfest ist die Hauptattraktion ein in acht gleich große Sektoren unterteiltes Glücksrad. Fünf der Sektoren sind rot, zwei grün und einer blau gefärbt. Zur Rotation gebracht, kommt das Rad nach kurzer Zeit zum Stillstand und eine der Farben erscheint in einem Fenster.
Bei einem Spiel wird das Glücksrad zweimal nacheinander zur Rotation gebracht. Erscheint beide Male der blaue Sektor, so erhält der entsprechende "Spieler" 10 Gummibärchen als Gewinn, bei zwei grünen Sektoren 8 Bärchen, bei zwei roten 3 Bärchen; in allen anderen Fällen wird 1 Bärchen als "Trostpreis" vergeben.
Die Zufallsgröße  Y  gibt die Anzahl der in einem Spiel gewonnenen Gummibärchen an.

4.1

Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsgröße  Y  und zeichnen Sie ein zugehöriges Histogramm.   (5 BE)

4.2

Berechnen Sie den Erwartungswert und die Standardabweichung der Zufallsgröße  Y.   (4 BE)

4.3

Ein Lausbub, der bereits bis 50 zählen kann, hat das Glücksrad "manipuliert", indem er heimlich einen Kaugummi auf die Rückseite des blauen Sektors geklebt hat. Er vermutet, dass der blaue Sektor nun häufiger erscheint (Gegenhypothese). Dazu beobachtet er 50 Drehungen des Rades und glaubt, seine Vermutung als bestätigt ansehen zu können, wenn dabei der blaue Sektor mehr als 10-mal erscheint.
Geben Sie die Testgröße, die Nullhypothese und die Gegenhypothese sowie die Art des vorliegenden Hypothesentests an.
Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Lausbub seine Vermutung als bestätigt betrachtet, obwohl das Rad durch den Kaugummi in Wirklichkeit nicht beeinflusst wird.   (5 BE)