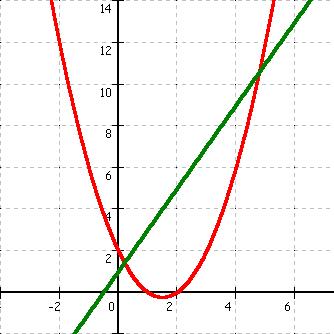
gegeben sind die Funktionen: g(x) = 2 * x + 1 und f (x) = x² - 3 * x + 2

Nun muss man die Terme der Funktionen gleichsetzen, um mit Hilfe der Mitternachtsformel ihre gemeinsamen Schnittpunkte errechnen zu können:

Somit wurde bewiesen, dass sich die Funktionen an 2 Punkten schneiden, das heißt die Gerade g(x) ist im Bezug auf die Parabel f (x) eine Sekante.

Um nun noch die Koordinaten der Schnittpunkte zu berechnen, setzt man einfach die eben erhaltenen x - Werte der Schnittpunkte in eine der 2 Funktionsgleichungen ein und erhält dann die y - Werte.

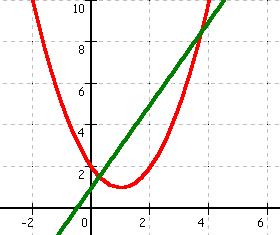
gegeben sind die Funktionen: h(x) = 2 * x + 1 und f (x) = x² - 2 * x + 2

Nun muss man die Terme der Funktionen gleichsetzen, um mit Hilfe der Mitternachtsformel ihre gemeinsamen Schnittpunkte errechnen zu können:

Somit wurde bewiesen, dass sich die Funktionen an 2 Punkten schneiden, das heißt die Gerade h(x) ist im Bezug auf die Parabel f (x) eine Sekante.

Um nun noch die Koordinaten der Schnittpunkte zu berechnen, setzt man einfach die eben erhaltenen x - Werte der Schnittpunkte in eine der 2 Funktionen ein und erhält dann die y - Werte.

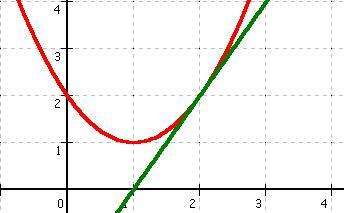
Damit aus der Geraden h(x) nun eine Tangente wird, darf die Gleichung, die durch das Gleichsetzen von h(x) und f (x) entstanden ist nur eine Nullstelle haben (das heißt: die Diskriminate der Mitternachtsformel muß 0 sein) !

Und da laut der Aufgabenstellung nur der Schnittpunkt mit der y - Achse geändert werden darf,

heißt das, dass sich nur t (y = m * x + t) ändern soll.

Damit weiß man, wenn man h(x) um eine Einheit auf der y - Achse nach oben verschiebt, dass aus h(x) im Bezug auf
f (x) eine Tangente wird.

Die Nullstelle der Gleichung, die durch das Gleichsetzen von der verschobenen h(x) und f (x) entsteht, entspricht der Berührstelle der beiden.

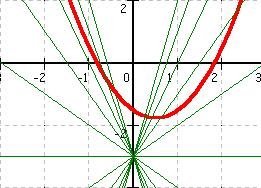
gegeben sind die Funktionen: g(x) = m * x - 3 (wir wissen ja, dass die Gerade die y - Achse auf jeden Fall im Punkt (0/-3) schneidet) und p (x) = x² - x - 1,5

Damit aus der Geraden g(x) nun eine Tangente wird, darf die Gleichung, die durch das Gleichsetzen von g(x) und p (x) entstanden ist nur eine Nullstelle haben (dass heißt: die Diskriminate der Mitternachtsformel muß 0 sein) !

Somit setze ich für die mir unbekannte Steigung der Geraden eine Variable ein und errechne diese dann mit Hilfe der Mitternachtsformel.

Also ist die Steigung der Geraden g entweder m = 1,45 oder m = - 3,45, wenn sie die Funktion p (x)berührt .

Damit nun aus der Geraden g(x) eine Sekante wird, muß die Gleichung, die durch das Gleichsetzen von g(x) und p (x) entstanden ist nun 2 Nullstellen haben (dass heißt: die Diskriminate der Mitternachtsformel muß größer als 0 sein) !

Somit setze ich für die mir unbekannte Steigung der Geraden wieder eine Variable ein und rechne diese dann mit Hilfe der Mitternachtsformel so aus, dass D > 0 ist.

Aus derLösung der Gleichung schließe ich auf die der Ungleichung:

D > 0 , wenn m < - 3,45 oder größer als 1,45 ist - (an einer Skizze sichtbar !)

sollte m > - 3,45, aber noch kleiner als 1,45 sein, so ist g(x) eine Passante.