Lösungen
1a)
f(x) = 2 * x4 - 5 * x3 + 3 * x2 + 4
h(x) = x2 - 2
![]() Gleichsetzen
zum Berechnen gemeinsamer Schnittpunkte !
Gleichsetzen
zum Berechnen gemeinsamer Schnittpunkte !
f(x) = h(x)
2 * x4 - 3 * x2 + 2 = x2 - 2
0 = 2 * x4 - 4 * x2 + 4
![]() Nullstellen
dieser Gleichung entsprechen den gemeinsamen Schnittpunkten von f(x)
und h(x) !
Nullstellen
dieser Gleichung entsprechen den gemeinsamen Schnittpunkten von f(x)
und h(x) !
0 = 2 * x4 - 4 * x2 + 4
![]() Rechnen vereinfachen durch den Einsatz des Substitutionsverfahren !
Rechnen vereinfachen durch den Einsatz des Substitutionsverfahren !
x² = z
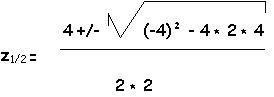
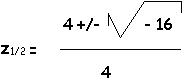
![]() Da
die Diskriminate ein negatives Vorzeichen hat, gibt es keine Nullstellen -
das heißt, f(x) und h(x)
haben keine gemeinsamen Schnittpunkte.
Da
die Diskriminate ein negatives Vorzeichen hat, gibt es keine Nullstellen -
das heißt, f(x) und h(x)
haben keine gemeinsamen Schnittpunkte.
 |
![]() Ableiten
!
Ableiten
!
|
Das heißt hier:
p(x) = f(x) - h(x)
p`(x) = f`(x) - h`(x)
p(x) = 2 * x4 - 4 * x2 + 4
p`(x) = 2 * 4 * x(4-1) - 4 * 2 * x(2-1) + 4 * 0 * x(0 -1)
p`(x) = 8 * x 3 - 8 * x
1b)
f(x) = 2 * x4 + 4 * x3 - x2
h(x) = - x3 + - 2 * x2
![]() Gleichsetzen
zum Berechnen gemeinsamer Schnittpunkte !
Gleichsetzen
zum Berechnen gemeinsamer Schnittpunkte !
f(x) = h(x)
2 * x4 + 4 * x3 - x2 = - x3 + - 2 * x2
0 = 2 * x4 + 5 * x3 + x2
![]() Nullstellen
dieser Gleichung entsprechen den gemeinsamen Schnittpunkten von f(x)
und h(x) !
Nullstellen
dieser Gleichung entsprechen den gemeinsamen Schnittpunkten von f(x)
und h(x) !
0 = 2 * x4 + 5 * x3 + x2
0 = x2 * (2 * x2 + 5 * x + 1)
x1/2 = 0
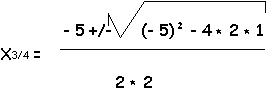
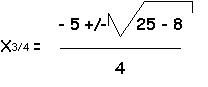
x3 = - 0,22
x4 = - 2,3
 |
![]() Ableiten
!
Ableiten
!
p(x) = f(x) - h(x)
p`(x) = f`(x) - h`(x)
p(x) = 2 * x4 + 5 * x3 + x2
p`(x) = 2 * 4 * x(4-1) + 5 * 3 * x(3-1) + 1 * 2 * x(2 -1)
p`(x) = 8 * x3 + 15 * x2 + 2 * x
2a)
f(x) = 3 * x4 - x3 + 4 * x
|
Das heißt hier:
h(x) = f(x) + c
h(x) = f(x) + 10
h(x) = 3 * x4 - x3 + 4 * x + 10
h`(x) = 3 * 4 * x(4-1) - 1 * 3 * x(3-1) + 4 * 1 * x(1 -1) + 10 * 0 * x(0 -1)
h`(x) = 1 2 * x3 - 3 * x2 + 4
2b)
f(x) = - 6 * x2 + 1,5 * x
h(x) = f(x) + c
h(x) = f(x) + 6
h(x) = - 6 * x2 + 1,5 * x + 6
h`(x) = - 6 * 2 * x(2-1) + 1,5 * 1 * x(1-1) + 6 * 0 * x(0 -1)
h`(x) = - 12 * x + 1,5