Aufgabe 1
Wertetabelle :
|
x
|
f(x)
|
|
0
|
0 |
|
1
|
1,1468
|
|
2
|
4,1920
|
|
3
|
8,5838
|
|
4
|
13,8240
|
|
5
|
19,4688
|
|
6
|
25,1280
|
|
7
|
30,4658
|
|
8
|
35,2000
|
|
9
|
39,1028
|
|
10
|
42,0000
|
|
11
|
43,7718
|
|
12
|
44,3520
|
|
13
|
43,7288
|
|
14
|
41,9440
|
|
15
|
39,0938
|
|
16
|
35,3280
|
|
17
|
30,8507
|
|
18
|
25,9200
|
|
19
|
20,8478
|
|
20
|
16,0000
|
|
21
|
11,7968
|
|
22
|
8,7120
|
|
23
|
7,2737
|
|
24
|
8,0640
|
|
25
|
11,7187
|
Graph:
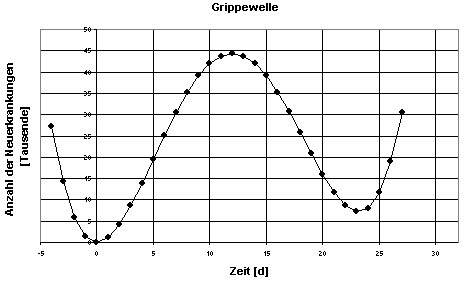
Aufgabe 2
f (x) = 0,00225x4– 0,1055x3 + 1,25x2
Ableitungen:
f´ (x) = 0,009x3– 0,3165x2 + 2,5x
f´´ (x) = 0,027x2– 0,633x + 2,5
2a ) Größte Zahl der Neuerkrankungen:
f´ (x) = 0,009x3– 0,3165x2 + 2,5x = 0
durch Ausklammern von x : --> x1 = 0
Polynomdivision: (0,009x3– 0,3165x2 + 2,5x) : x = 0,009 x2 – 0,3165x + 2,5
Mitternachtsformel:
x 2 = 23,19
x 3 = 11,98
| Mon.ber. | - <
x < |
0 | < x < | 11,98 | < x < | 23,19 | < x < |
| f´ | - | + | - | + | |||
| Gf | fällt | TP1 | steigt | HP | fällt | TP2 | steigt |
Der Hochpunkt der Funktion liegt bei x = 11,98 d, also ist am 12. Tag
die Zahl der Neuerkrankungen am größten.
f (12) = 0,00225x4– 0,1055x3+ 1,25x2
= 44,3520
Die gemessene Anzahl
der Neuerkrankungen am 12. Tag liegt bei ca. 44350.
2 b ) Stärkster Anstieg der Neuerkrankungen
f´´ (x) = 0,027x2 – 0,633x + 2,5 = 0
x 1 = 18,42
x 2 = 5,03
| Kr.ber. | -<
x < |
5,03 | < x < | 18,42 | < x < |
| f´´ | + | - | + | ||
| Gf | links | WP1 | rechts | WP2 | links |
Der WP1 ist der Punkt mit der höchsten Steigung, somit
ist zu Beginn des 6. Tages der stärkste Anstieg an Neuerkrankungen.
Die Zuwachsrate ist
bzw f'(x)
y = f (6) – f(5) = 25,128– 19,469 = 5,659
x = 1 d
ca. 5650 Neuerkrankungen
an diesem Tag mehr als am Vortag.
Je kleiner die Zeitdifferenz, desto genauer wird die Aussage.
oder einfacher: f'(5)
= 5710
2c )
Vor Tag 0 wurden keine Messungen durchgeführt.
Während die Funktionskurve
für negative x gegen
geht, ist die Anzahl der Neuerkrankungen vor der Grippewelle ca. 0
Nach dem TP2
bei 23,19 d steigt die Funktionskurve an und geht gegen ,
während die Anzahl der Neuerkrankungen nach der Grippewelle ausklingt
und gegen 0 geht.
2d ) Auslauf
des Graphen
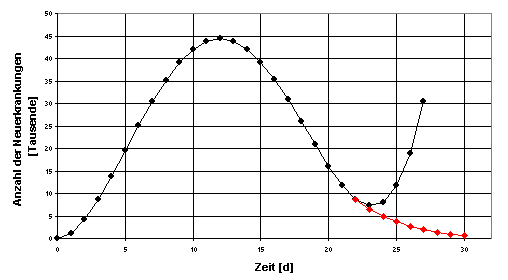
2e ) Rückgang der Grippekranken
Formulierung einer Funktion g (x) der Genesungswelle (Erkrankungswelle um 8 Tage verschoben) :
f (x) = 0,00225x4 – 0,1055x3 + 1,25x2
g (x) = 0,00225 (x-8)4
– 0,1055 (x-8)3 + 1,25 (x-8)2
mit Definitionsbereich [8/30]
Neuerkrankungen und
Genesungen
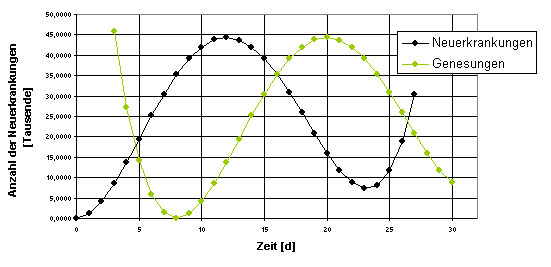
Schnittpunktberechnung:
f (x) = g (x)
0,00225x4 – 0,1055x3 + 1,25x2 = 0,00225 (x-8)4 – 0,1055 (x-8)3 + 1,25 (x-8)2
Auf eine rechnerische
Lösung soll verzichtet werden. Graphisch ergibt sich die Lösung
aus dem Schnittpunkt im Bereich [8/22] (=Schnittmenge der Definitionsbereiche):
x2 ≈ 16
Das heißt, nach Tag 16 kann mit einem Rückgang der Grippekranken
gerechnet werden.
2 f)
Krankenschätzung: (grob anhand der Zeichnung)
Es ist die Summe der innerhalb der letzten acht Tage Erkrankten
|
Tag
|
Kranke
in Tsd.
|
|
23
|
7,0
|
|
24
|
5,5
|
|
25
|
4,5
|
|
26
|
3,5
|
|
27
|
3,0
|
|
28
|
2,5
|
|
29
|
2,0
|
|
30
|
1,5
|
|
Gesamt
|
ca 30.000
|
