Hochwasseraufgabe
(als Beispiel für "lokale Änderungsrate")
Gegeben ist folgende Funktion p(t), die den Pegelstand eines Flusses in der Zeit vom 1. – 10. August näherungsweise beschreibt.
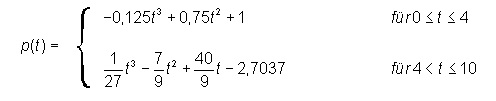
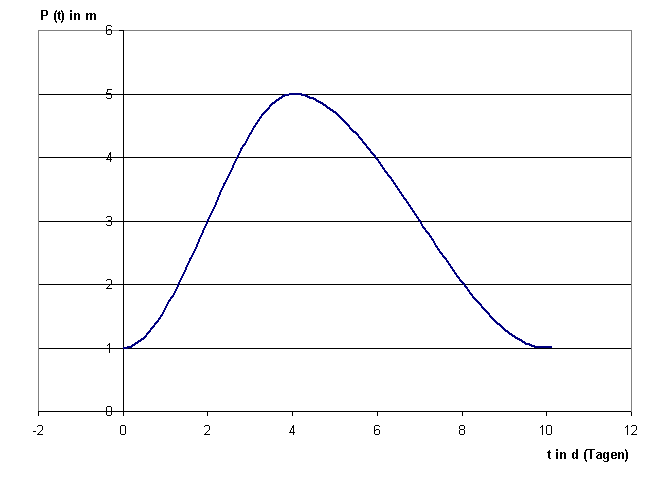
Aufgabe 1
Beschreiben Sie den zeitlichen Verlauf des Hochwassers. Gehen Sie dabei auch darauf ein, wann die Pegelstandsänderung am größten ist.
Aufgabe 2
Welche Uhrzeit entspricht t1 = 0,5 d bzw. t2= 0,6 d , wenn t = 0 am 1. August um 0.00 Uhr gilt?
Aufgabe 3
Berechnen
Sie den Anstieg des Pegelstands zwischen 0,5 d und 0,6 d. In welcher Einheit
wird er gemessen?
Welche andere
Einheit wäre evtl. anschaulicher bzw. angemessener?
Aufgabe 4
Berechnen Sie p´(t) = dp / dt als abschnittsweise definierte Funktion und lassen Sie den Graphen von p´ vom Programm WINFUNKTION (oder einem anderen Programm) zeichnen.
Aufgabe 5
Berechnen Sie p´(0,5) und vergleichen Sie den Wert mit den Ergebnissen von Aufgabe 3. Was fällt auf? Geben Sie die Bedeutung von p´ ( t ) im Kontext der Aufgabe an.
Aufgabe 6
Wann ist
der Pegelstandsanstieg am größten. Wie viel cm steigt er zu
diesem Zeitpunkt pro Stunde bzw. pro Minute? Wie hoch ist der Pegelstand
selbst zu diesem Zeitpunkt?
Markieren Sie den zugehörigen Punkt im Graphen von p.
Aufgabe 7
a
) Bestimmen Sie p´´( t ) rechnerisch.
b ) Berechnen Sie, wann p´´( t) = 0 gilt.
Um welche besonderen Zeitpunkte handelt es sich dabei? (vgl. Aufg. 1 und
6)
Aufgabe 8
Erstellen
Sie nun eine Vorzeichentabelle für p´( t) und p´´(t).
Beschreiben Sie die Änderung des Pegelstandes in den einzelnen Zeitabschnitten
mit Worten.
0
< t < |
2 |
<
t < |
4 |
<
t< |
7 |
<
t < 10 |
|
| p´ ( t ) | |||||||
| p´´( t ) | |||||||
| Das Hochwasser |