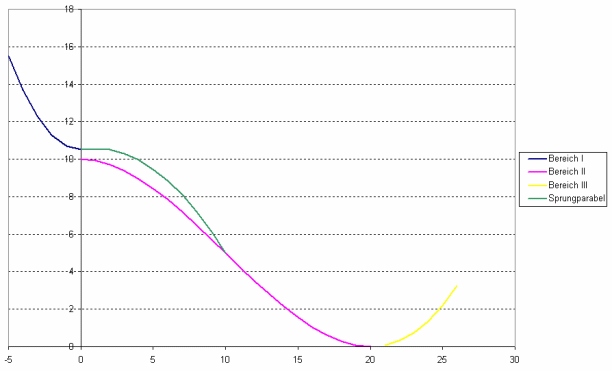
Skisprung Antworten

Aufgabe 1

z.B.

für Bereich I:

für Bereich II:

für Bereich III:

Aufgabe 2

a ) in mathematischer Hinsicht: Sprungstelle

b ) in sportlicher Hinsicht: Sprungtisch-kante

d.h. es handelt sich in beiden Fällen um eine „Sprungstelle“

Aufgabe 3

Der Funktionswert an der Übergangsstelle muss mit dem linksseitigen Grenzwert (aus Bereich II) und dem rechtsseitigen Grenzwert (aus Bereich III) übereinstimmen, d.h. es liegt keine Sprungstelle vor (Stetigkeit).

Die Steigung muss im Grenzwert von links (1.Ableitung im Bereich II) und von rechts (1.Ableitung im Bereich III) übereinstimmen, d.h. es liegt kein Knick vor (Differenzierbarkeit).

Stetigkeit (bzw.Sprung)

Bereich II (eigentlich trivial)

Bei Polynomfunktionen ist grundsätzlich der Grenzwert gleich dem Funktionswert, also
x = 20 einsetzen:

Bereich III

Die Kurve ist an der Stelle x = 20 stetig.

Differenzierbarkeit („Knick“)

Bereich II

1. Ableitung von Bereich II :

Auch hier gilt wie oben: Grenzwert gleich y-Wert:

Bereich III



1. Ableitung von Bereich III :

Die Kurve ist an der Stelle x = 20 differenzierbar.

Ja: Das Gelände macht dort keinen „Knick“, der den Springer zum „Stolpern“ veranlassen könnte.

Aufgabe 4.1


Keinen Knick sollte es geben, wenn der Springer sich einfach über das Ende der Schanze gleiten läßt. Da der Springer aber eine Sprungbewegung ausführt, die seinen Körperschwerpunkt weiter nach oben bringt, ist hier ein Knick zu erwarten.
Überprüfung ob es einen „Knick“ an der Absprungstelle gibt:

Stetigkeit

Bereich I

Bereich bis a:

Die Bewegungskurve des Sportlers ist (in unserem Modell!) für x = 0 stetig.


Differenzierbarkeit

Bereich I

1. Ableitung von Bereich I :

Bereich bis a

1. Ableitung von Bereich bis a

Die Bewegungskurve ist für x = 0 aber nicht differenzierbar.

Aufgabe 4.2

Aufsprungstelle x = a

Schnittpunktberechnung

Gleichsetzen:

Bereich bis a = Bereich II

Umformung:

Durch raten: x₁ = 10

Polynomdivision:

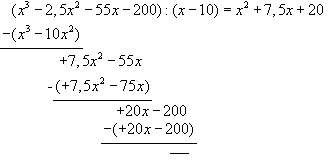
keine weitere Lösung, daher a = 10

Dies ist nur die horizontale Entfernung vom Schanzenende, nicht aber die Flugweite.

Aufgabe 4.3

Scheitelpunktberechnung:

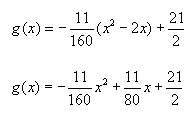
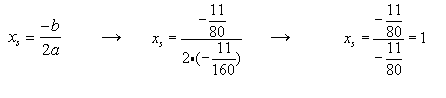
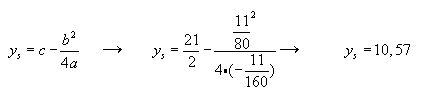
Aufgabe 4.4

Sprungparabel