Skisprung-Aufgaben

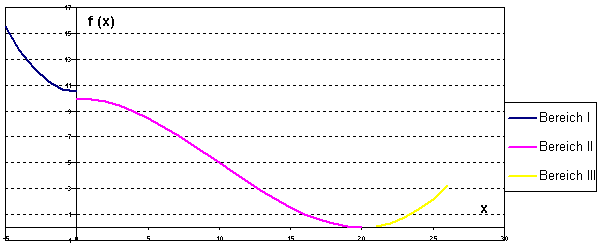
Der folgende Graph zeigt das Seitenprofil einer Sprungschanze mit Aufsprunghügel und Auslauf:

Aufgabe 1

Überprüfen Sie durch Berechnen geeigneter Funktionswerte, dass die folgende abschnittsweise definierte Funktion f eine brauchbare Näherungsfunktion für das „Seitenprofil“ darstellt:

f : x f(x) =

Bereich I :
Bereich II :
Bereich III:

Aufgabe 2

Erläutern Sie, welche besondere Stelle bei x = 0

a) in mathematischer Hinsicht

b) in Hinsicht auf einen Skispringer vorliegt.

Aufgabe 3

Zeigen Sie rechnerisch, dass der Graph vom Bereich II (also dem Aufsprunghügel) glatt, das heißt ohne „Knick“ in den Bereich III (also den Auslauf) übergeht. Ist dieses Ergebnis auch für den Skispringer wichtig?

Aufgabe 4.0

Martin Schmidt stellt bei einem seiner Sprünge von der obigen Schanze einen neuen Schanzenrekord auf. Ein Fernsehteam hat den Sprung aufgezeichnet und analysiert. Es zeigt sich, dass sich seine (natülich ideale!) Sprungkurve sehr genau durch ein Parabelstück beschreiben lässt, sein gesamter von der Seite her aufgenommener „Bewegungsablauf“ (Anlauf, Sprung, Landung, Auslauf) daher durch die folgende Funktion angenähert werden kann:

g : x g(x) =

Bereich bis 0 :
Bereich bis a :
Bereich bis 30:

Aufgabe 4.1

Überlegen Sie zunächst, ob die Bewegungskurve des Sportlers (in unserem Modell) an der Absprungstelle x = 0 einen Knick aufweisen wird. Überprüfen Sie dann ihre Vermutung rechnerisch.

Aufgabe 4.2

Berechnen Sie die Aufsprungstelle x = a. Geben Sie den zugehörigen Wert auch in Metern an. Haben Sie damit nun die Weite des Rekordflugs berechnet?

Aufgabe 4.3

Berechnen Sie den Scheitelpunkt der Sprungparabel.

Aufgabe 4.4

Tragen Sie die Sprungparabel mit Farbe in obige Zeichnung ein. Verwenden Sie dazu bekannte Ergebnisse und berechnen Sie falls nötig weitere Funktionswerte.