a)

=> S (0 |-1)

 

b)

 

c)

Da sowohl x als auch die Konstante (c) fehlt:

=> S (0 | 0)

 

 

e)

=> S (-2 |-1)

 

f)

 

2.1

Nullstellen einer Funktion sind dort, wo der Graph die x-Achse schneidet oder berührt. Es sind Punkte mit der y-Koordinate null. Bei einer quadratischen Funktion können die Lösungen mit Hilfe folgender Formel berechnet werden:

Die Anzahl der Lösungen hängt von dem Term unter der Wurzel, der Diskriminante D = b² - 4ac ab.

Es gilt:

• D > 0 2 Nullstelle
• D = 0 1 Nullstelle
• D < 0 keine Nullstelle

Wenn man die Formel zur Lösung der quadratischen Gleichung anwenden will, sollte man zuerst die Diskriminante D berechnen. Dann kennt man bereits die Anzahl der Lösungen.

a)

D = b² - 4ac

D = 1 + 24 = 25 > 0

 

b)

Da x und Konstante (c) fehlt:

c)

D = 1681 > 0

d)

Wenn die Konstante (c) fehlt, tritt ein Spezialfall auf. Man kann das x und auch den Öffnungsfaktor ausklammern und die Nullstellen ablesen. Beide Faktoren müssen 0 ergeben!

e)

f)

Wenn das x-Glied fehlt, tritt ein weiterer Spezialfall auf. Man kann nach x auflösen. Dabei muss man allerdings bedenken, dass man aus negativen Zahlen nicht die Wurzel ziehen darf und dass eine quadratische Gleichung 2 Lösungen enthält.

g)

h)

-2 (x² + 1) + 2 (-2 + 2)x = 0

-2x² - 2 = 0

D = 0² - 4 · (-2) · (-2)

D = - 16 < 0

=> keine Nullstellen!

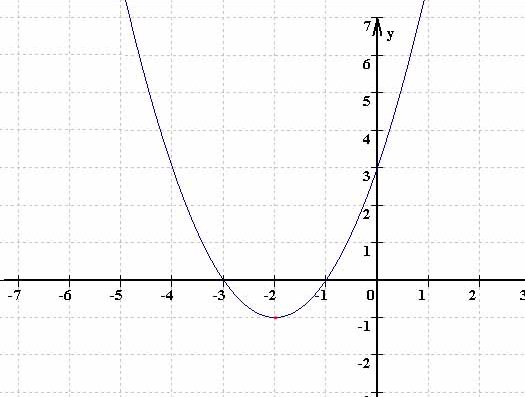
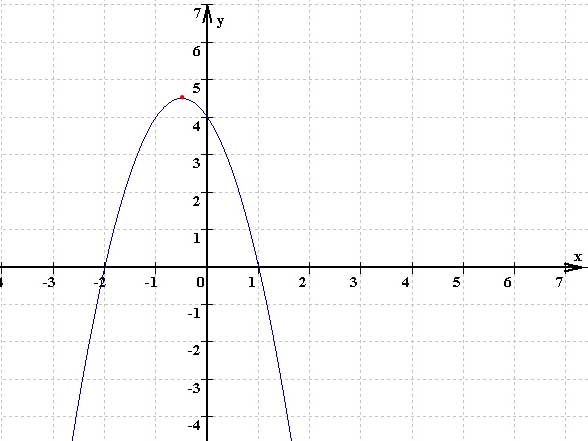
2.2

Da die Parabeln achsensymmetrisch sind, liegt die x-Koordinate des Scheitels genau in der Mitte zwischen den Nullstellen, d.h. es gilt:

a)

0,5 · ( 2 -3 ) = - 0,5

=> Die Parabel ist symmetrisch zur Geraden mit der Gleichung x = -0,5.

b)

Die Parabel ist symmetrisch zur y-Achse.

c)

0,5 · ( -0,2 - 2,25 ) = -1,225

=> Die Parabel ist symmetrisch zur Geraden mit der Gleichung x = -1,225

d)

0,5 · ( 0+4 ) = 2

=> Die Parabel ist symmetrisch zur Geraden mit der Gleichung x = 2

e)

f)

0,5 · (-4 + 4 ) = 0

Die Parabel ist symmetrisch zur y-Achse.

g)

Die Parabel ist symmetrisch zur y-Achse.

h)

Die Parabel ist symmetrisch zur y-Achse.