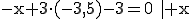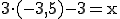1. Geraden in der Ebene
1.1 Vektorform
Für die Darstellung der Vektorform benötigen wir einen Punkt P als Stützpunkt, bzw. den Stützvektor 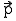 . Bei dem Stützpunkt handelt es sich um einen beliebigen Punkt, der auf der Geraden liegt. Desweitern benötigen wir den Vektor
. Bei dem Stützpunkt handelt es sich um einen beliebigen Punkt, der auf der Geraden liegt. Desweitern benötigen wir den Vektor  , der in Richtung der Geraden verläuft und Richtungsvektor genannt wird. Legen wir nun den Richtungsvektor an den Stützpunkt und strecken ihn mittels des reellen Streckungsfaktors r, so können wir vom Ursprung aus vektoriell jeden Punkt X auf der Geraden erreichen.
, der in Richtung der Geraden verläuft und Richtungsvektor genannt wird. Legen wir nun den Richtungsvektor an den Stützpunkt und strecken ihn mittels des reellen Streckungsfaktors r, so können wir vom Ursprung aus vektoriell jeden Punkt X auf der Geraden erreichen.
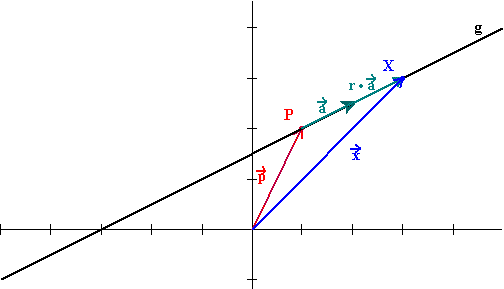
Es ergibt sich nämlich 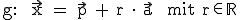
Hinweis: Ist statt  ein zweiter Geradenpunkt Q gegeben, so kann man mit Hilfe von P und Q den Richtungsvektor
ein zweiter Geradenpunkt Q gegeben, so kann man mit Hilfe von P und Q den Richtungsvektor 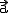 leicht bestimmen:
leicht bestimmen: 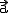 =
= 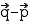 .
.
Beispiele:
Gegeben ist die Gerade g, die durch den Punkt P(3/3) geht, mit dem Richtungsvektor 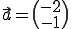 . Für
. Für 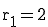 soll der dazugehörige Punkt
soll der dazugehörige Punkt 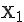 gesucht werden .
gesucht werden .
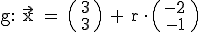 . Für
. Für 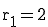 erhält man nun
erhält man nun 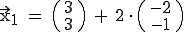 , also
, also
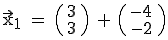 . Damit ist
. Damit ist 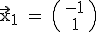 und
und 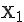 (-1/1) ist ein Punkt auf der Geraden g.
(-1/1) ist ein Punkt auf der Geraden g.
Genau so ist es möglich, für den Punkt 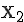 (-3/0), der ebenfalls auf der Geraden g liegt, das dazugehörige
(-3/0), der ebenfalls auf der Geraden g liegt, das dazugehörige 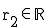 zu finden:
zu finden:
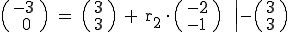
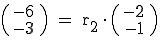
An dieser Stelle müssen wir die obere Gleichung in zwei Gleichungen aufteilen:
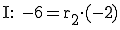
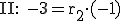
Sowohl für I also auch für II gilt 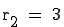 .
.
Siehe auch: Applets "Parameterdarstellung von Geraden" und "Raumgeraden in vektorieller Darstellung "
1.2 Koordiatenform
Wenn wir eine Gerade g in der Ebene haben, die durch einen Punkt 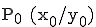 verläuft und den Richtungsvektor
verläuft und den Richtungsvektor  hat, lässt sich für einen beliebigen Punkt X (x/y) folgende Gleichung aufstellen:
hat, lässt sich für einen beliebigen Punkt X (x/y) folgende Gleichung aufstellen:
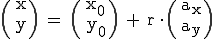
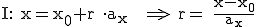
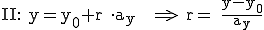
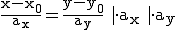
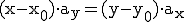
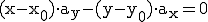
Diese Form wird auch als parameterfrei bezeichnet, da kein r mehr vorhanden ist.
Ausmulipliziert ergibt dies: 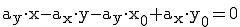
Ersetzt man nun  durch a,
durch a,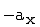 durch b und
durch b und 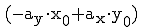 durch d, so erhält man die allgemeine parameterfreie Gleichung einer Geraden in der Ebene, auch Koordinatenform genannt:
durch d, so erhält man die allgemeine parameterfreie Gleichung einer Geraden in der Ebene, auch Koordinatenform genannt: 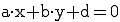 .
.
Beispiele:
Gegeben ist die Koordinatenform der Geraden 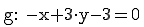
Prüfen Sie, ob der Punkt 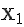 (3/2) auf g liegt.
(3/2) auf g liegt.
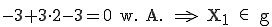
Bestimmen Sie x so, dass der Punkt 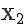 (x /-3,5) auf der Geraden g liegt.
(x /-3,5) auf der Geraden g liegt.
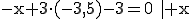
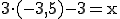
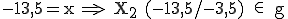
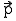 . Bei dem Stützpunkt handelt es sich um einen beliebigen Punkt, der auf der Geraden liegt. Desweitern benötigen wir den Vektor
. Bei dem Stützpunkt handelt es sich um einen beliebigen Punkt, der auf der Geraden liegt. Desweitern benötigen wir den Vektor 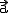 , der in Richtung der Geraden verläuft und Richtungsvektor genannt wird. Legen wir nun den Richtungsvektor an den Stützpunkt und strecken ihn mittels des reellen Streckungsfaktors r, so können wir vom Ursprung aus vektoriell jeden Punkt X auf der Geraden erreichen.
, der in Richtung der Geraden verläuft und Richtungsvektor genannt wird. Legen wir nun den Richtungsvektor an den Stützpunkt und strecken ihn mittels des reellen Streckungsfaktors r, so können wir vom Ursprung aus vektoriell jeden Punkt X auf der Geraden erreichen.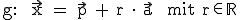
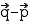 .
.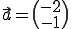 . Für
. Für 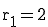 soll der dazugehörige Punkt
soll der dazugehörige Punkt 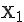 gesucht werden .
gesucht werden . 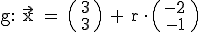 . Für
. Für 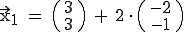 , also
, also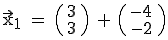 . Damit ist
. Damit ist 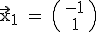 und
und 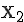 (-3/0), der ebenfalls auf der Geraden g liegt, das dazugehörige
(-3/0), der ebenfalls auf der Geraden g liegt, das dazugehörige 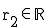 zu finden:
zu finden: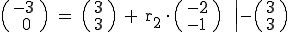
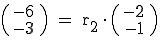
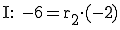
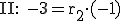
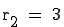 .
.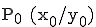 verläuft und den Richtungsvektor
verläuft und den Richtungsvektor  hat, lässt sich für einen beliebigen Punkt X (x/y) folgende Gleichung aufstellen:
hat, lässt sich für einen beliebigen Punkt X (x/y) folgende Gleichung aufstellen: 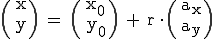
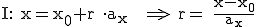
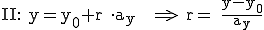
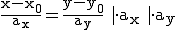
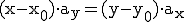
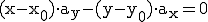
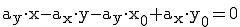
 durch a,
durch a,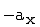 durch b und
durch b und 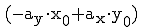 durch d, so erhält man die allgemeine parameterfreie Gleichung einer Geraden in der Ebene, auch Koordinatenform genannt:
durch d, so erhält man die allgemeine parameterfreie Gleichung einer Geraden in der Ebene, auch Koordinatenform genannt: 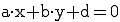 .
.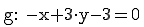
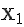 (3/2) auf g liegt.
(3/2) auf g liegt.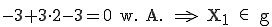
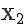 (x /-3,5) auf der Geraden g liegt.
(x /-3,5) auf der Geraden g liegt.