2. Geraden im Raum
Hier ist es sinnvoll, sich erst einmal mit dem dreidimensionalen Koordinatensystem vertraut zu machen:
Die z-Achse ist neu hinzugekommen. Die x-Achse wird auch als 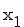 -Achse, die y-Achse als
-Achse, die y-Achse als 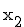 -Achse und die z-Achse als
-Achse und die z-Achse als 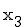 -Achse bezeichnet.
-Achse bezeichnet.
Siehe auch: Applets "3-Vektoren kennenlernen", "Räumliche Koordinaten" und "Komponenten eines Vektors "
Es ändert sich nichts an unserer alten Form 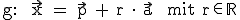 . Alle Vektoren haben im Raum noch einen zusätzlichen Wert, den z-Wert. Die Vektorform im dreidimensionalen Raum sieht wie folgt aus:
. Alle Vektoren haben im Raum noch einen zusätzlichen Wert, den z-Wert. Die Vektorform im dreidimensionalen Raum sieht wie folgt aus:
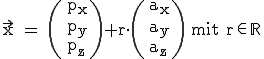 .
.
Hinweis: Ist statt 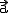 ein zweiter Geradenpunkt Q gegeben, so kann man mit Hilfe von P und Q den Richtungsvektor
ein zweiter Geradenpunkt Q gegeben, so kann man mit Hilfe von P und Q den Richtungsvektor 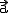 leicht bestimmen:
leicht bestimmen: 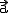 =
= 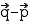 .
.
Beispiele:
Gegeben ist eine Gerade g im Raum, die durch den Punkt P(-1 / 4 / 2) verläuft und den Richtungsvektor 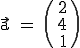 hat. Für
hat. Für 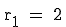 soll der dazugehörige Punkt
soll der dazugehörige Punkt  gesucht werden.
gesucht werden.
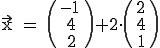
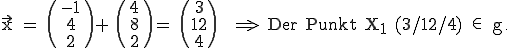
Überprüfung, ob der Punkt 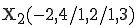 auf der Gerade g liegt:
auf der Gerade g liegt:
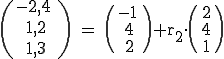

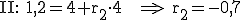
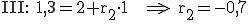
Da jedesmal derselbe 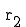 -Wert resultiert, liegt
-Wert resultiert, liegt 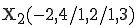 auf der Geraden g.
auf der Geraden g.
Für die Gerade im Raum gibt es keine Koordinatenform!
Eine Gerade kann folgende besondere Lagen im Raum annehmen:
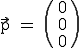 )
)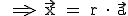
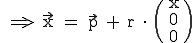
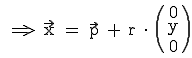
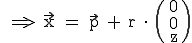
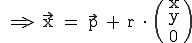
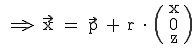
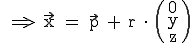
| Weiter zu Ebenen im Raum | Zurück zur Übersicht |