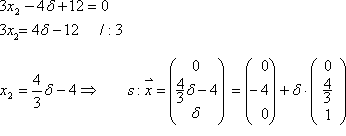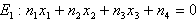 ,
, 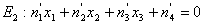
1.3.3 Beide Ebenen in Koordinatenform
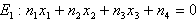 ,
, 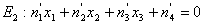
(1) 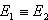
Beispiel:
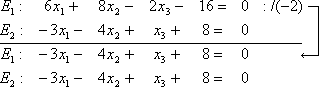
Gilt nach der Umformung 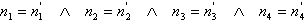 ,
,
so fallen die Ebenen zusammen d.h. sie sind identisch.
Es gilt: 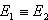 .
.
(2) 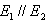
Beispiel:
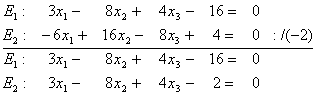
Gilt nach der Umformung 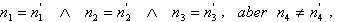
so sind die beiden Ebenen echt parallel.
Es gilt: 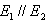 .
.
(3) 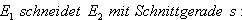
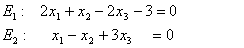
Zunächst erkennt man, dass die Ebenen nicht parallel sind, sich also in einer Geraden schneiden.
Berechnung der Schnittgeraden:
1.Möglichkeit:
Für eine der drei Variablen wird der Streckungsparameter der Schnittgeraden eingesetzt,
also z.B. 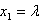 .
.
Dann ergint sich das LGS:
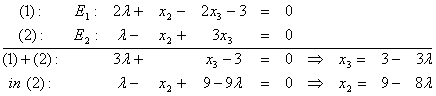
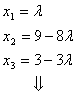
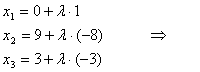
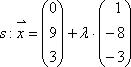
2.Möglichkeit:
Die Schnittgerade wird über ihre Spurpunkte, also ihre Schnittpunkte
mit den Koordinatenebenen, bestimmt.
Für den Spurpunkt 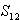 mit
der
mit
der 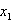
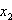 -Koordinatenebene ist
-Koordinatenebene ist 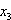 = 0 .
= 0 .
Für den Spurpunkt 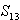 mit
der
mit
der 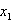
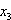 -Koordinatenebene ist
-Koordinatenebene ist 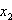 = 0 .
= 0 .
Für den Spurpunkt 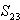 mit
der
mit
der 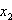
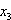 -Koordinatenebene ist
-Koordinatenebene ist 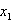 = 0 .
= 0 .
Bestimmung von 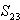 :
:
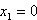 in
in 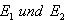 :
:
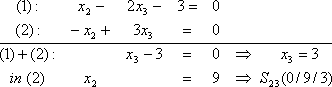
Bestimmung von 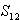 :
:
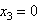 in
in 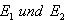 :
:
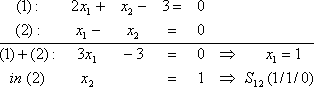
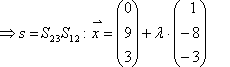
Sonderfall:
Eine Ebene wird auf einfache Weise mithilfe ihrer Spurgeraden gezeichnet.
Die Spurgeraden sind die Schnittgeraden mit den Koordinatenebenen
Beispiel:
Bestimmung der Spurgerade der Ebene E: 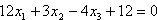 in der
in der 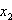
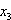 -Koordinatenebene:
-Koordinatenebene:
Man setzt in E 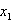 = 0 ein,
also
= 0 ein,
also 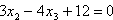
Mit 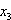 =
= 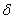 erhält
man hieraus:
erhält
man hieraus: