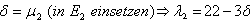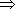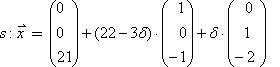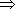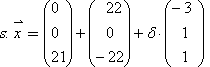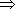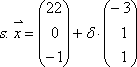1.3 Lagebeziehung zwischen Ebene und Ebene
Welche Lagebeziehungen sind zwischen zwei Ebenen möglich?
1.3.1 Beide Ebenen in Parameterform
(1) 
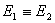
Beispiel:
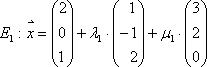
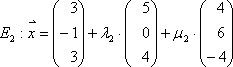
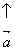
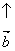
Gleichsetzen: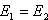 
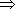
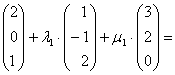
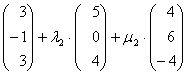
Umformen: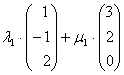 
= 
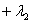
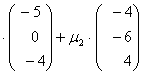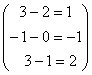
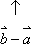
Gauß: 
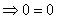: wahre Aussage
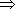die Ebenen sind identisch !
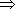Es
gilt:
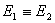
(2) 
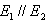
Beispiel:
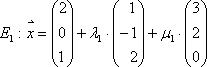
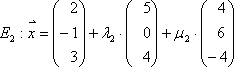
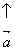
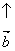
Gleichsetzen: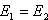 
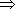
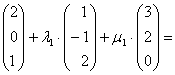
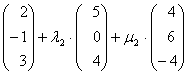
Umformen: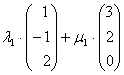 
=
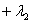
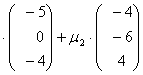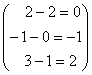
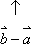
Gauß: 
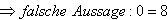, d. h. das
LGS hat keine Lösung.
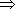die Ebenen haben keine gemeinsamen Punkte
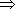
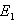ist
parallel zu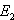 
,
aber nicht identisch. Man nennt die beiden Ebenen echt parallel.
Es gilt: 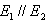und
E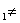
.
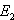(3) 
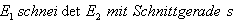
Beispiel:
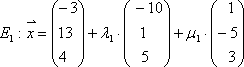
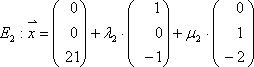
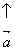
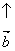
Gleichsetzen: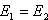 
=
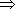
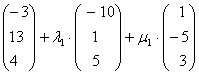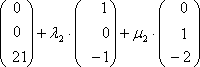
Umformen: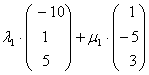 
+
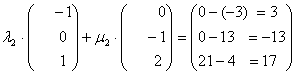
Gauß: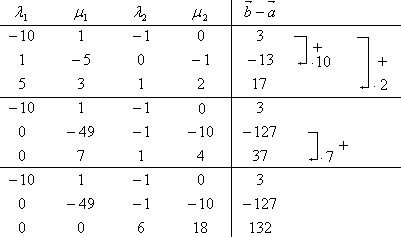 
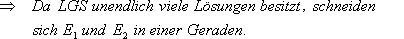
Berechnung der Schnittgerade: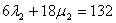 
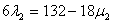
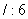
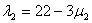
Setze z.B. 
