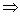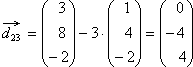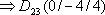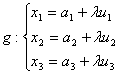 in die Ebene E ein.
in die Ebene E ein.1.2.2 Ebene in Koordinatenform
Vorgehensweise:
Man setzt die Koordinaten der Punkte der Geraden 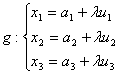 in die Ebene E ein.
in die Ebene E ein.
(1) g liegt in E:
Beispiel: E: 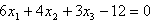 ,
,
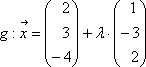
Lösung: 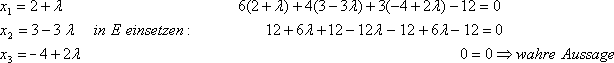
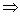 Die Ausdrücke mit dem Parameter (hier
Die Ausdrücke mit dem Parameter (hier ) fallen weg und es bleibt eine wahre Aussage stehen
) fallen weg und es bleibt eine wahre Aussage stehen
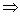 Die Gerade g liegt in der Ebene E, weil sich für jeden Wert des Parameters beim Einsetzen
Die Gerade g liegt in der Ebene E, weil sich für jeden Wert des Parameters beim Einsetzen
in E eine wahre Aussage ergibt, d.h. jeder Punkt der Geraden liegt in der Ebene.
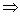 Es gilt:
Es gilt: 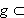 E .
E .
(2) g parallel zu E:
Beispiel: E: 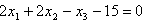 ,
,
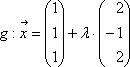
Lösung: 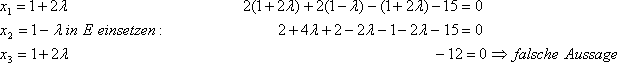
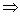 Die Ausdrücke
mit dem Parameter (hier
Die Ausdrücke
mit dem Parameter (hier )
fallen weg und es bleibt eine falsche Aussage stehen
)
fallen weg und es bleibt eine falsche Aussage stehen
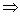 Die Gerade
g ist echt parallel zur Ebene E, weil sich für jeden Wert des Parameters beim
Die Gerade
g ist echt parallel zur Ebene E, weil sich für jeden Wert des Parameters beim
Einsetzen in E eine falsche Aussage ergibt, d.h. kein Punkt
der Geraden liegt in der Ebene.
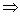 Es gilt: g || E .
Es gilt: g || E .
(3) g schneidet E im Schnittpunkt S:
Beispiel: E: 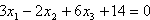 ,
,
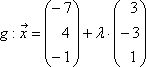
Lösung: 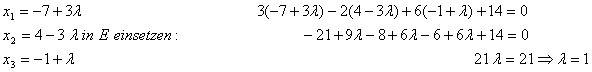
Berechnung des Schnittpunktes:
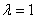 in
g einsetzen :
in
g einsetzen :
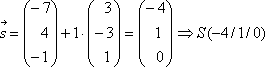
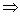 Errechnet sich
für den Parameter (hier
Errechnet sich
für den Parameter (hier )
ein Wert, dann schneidet die Gerade g die Ebene
)
ein Wert, dann schneidet die Gerade g die Ebene
in einem Punkt S.
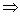 Es gilt: g
Es gilt: g 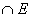 = {S}
= {S}
Sonderfälle:
1. Bestimmung der Schnittpunkte (Durchstoßpunkte) der Koordinatenachsen mit einer Ebene:
Beispiel:: E: 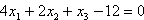
Schnittpunkt mit 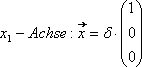
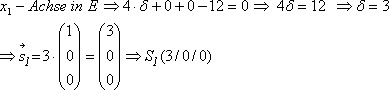
Schnittpunkt mit 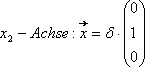
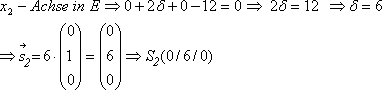
Schnittpunkt mit 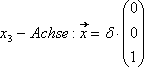
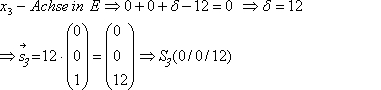
2. Bestimmung der Schnittpunkte (Durchstoßpunkte) einer Geraden durch die Koordinatenebenen
Diese Schnittpunkte nennt man Spurpunkte.
Die Berechnung ist recht einfach, wenn die Koordinatenebenen in Koordinatenform
gegeben sind.
Beispiel: 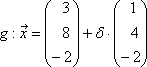
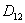 = Schnittpunkt
der Gerade mit
= Schnittpunkt
der Gerade mit 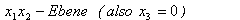
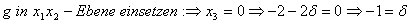
Berechnung des Schnittpunktes: Einsetzen von 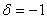 in g:
in g:
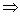
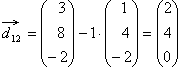

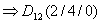
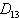 = Schnittpunkt
der Gerade mit
= Schnittpunkt
der Gerade mit 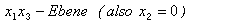
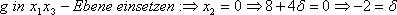
Berechnung des Schnittpunktes: Einsetzen von 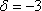 in g:
in g:
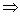
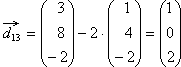

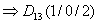
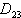 = Schnittpunkt
der Gerade mit
= Schnittpunkt
der Gerade mit 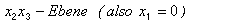
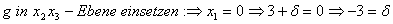
Berechnung des Schnittpunktes: Einsetzen von 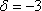 in g:
in g: