
1. Lagebeziehungen zwischen Geraden und Ebenen
1.1. Lagebeziehung zwischen zwei Geraden im IR2 bzw. im IR3
Fangen wir mit den Geraden an: Wie können 2 Geraden g und h zueinander liegen?

Gegeben sind nun die beiden Geraden in der folgenden Form:
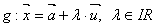 und
und 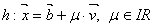 .
.
Untersuchung auf Parallelität:
Gibt es ein 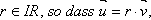 dann sind die Richtungsvektoren von g und h Vielfache voneinander.
dann sind die Richtungsvektoren von g und h Vielfache voneinander.
In diesem Fall verlaufen g und h parallel.
Untersuchung auf Identität: ( man wählt einen Punkt A oder B)
Gibt es im Fall der Parallelität z. B. ein 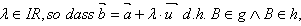 dann sind g und h identisch (fallen zusammen).
dann sind g und h identisch (fallen zusammen).
Andernfalls sind g und h echt parallel.
Gibt es kein 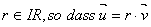 , dann sind die Richtungsvektoren keine Vielfachen voneinander.
, dann sind die Richtungsvektoren keine Vielfachen voneinander.
In diesem Fall sind g und h nicht parallel.
Untersuchung auf die Existenz eines Schnittpunktes:
Gibt es genau ein 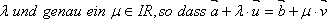 , so schneiden sich g und h in einem Punkt, nämlich ihrem Schnittpunkt.
, so schneiden sich g und h in einem Punkt, nämlich ihrem Schnittpunkt.
Ist hingegen die genannte Gleichung nicht lösbar, so besitzen g und h keinen gemeinsamen Punkt.
In diesem Fall sind g und h windschief.
Bei der Untersuchung der Lage zweier Geraden zueinander untersucht man also zuerst auf Parallelität.
Sind die Geraden dann parallel, so kontrolliert man, ob sie einen gemeinsamen Punkt besitzen. Sie sind dann entweder identisch (fallen zusammen) oder echt parallel.
Sind die Geraden nicht parallel, so müssen sie sich im  schneiden. Im
schneiden. Im  überprüft man, ob sie einen gemeinsamen Punkt besitzen. Es ergibt sich, dass sie sich entweder schneiden oder windschief sind.
überprüft man, ob sie einen gemeinsamen Punkt besitzen. Es ergibt sich, dass sie sich entweder schneiden oder windschief sind.
Beispiele:
Bestimme jeweils die gegenseitige Lage der beiden Geraden g und h:
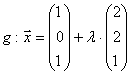 ,
, 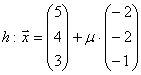
Lösung:
Untersuchung auf Parallelität:

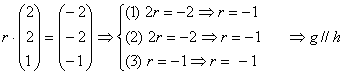
Untersuchung auf Identität:
A(1/0/1) in h:
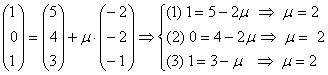
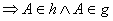
 Der Punkt A(1/0/1) liegt sowohl auf der Geraden h, als auch auf der
Geraden g.
Der Punkt A(1/0/1) liegt sowohl auf der Geraden h, als auch auf der
Geraden g.
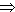 g = h. Damit sind g und h identisch (sie fallen zusammen).
g = h. Damit sind g und h identisch (sie fallen zusammen).
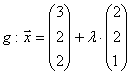 ,
, 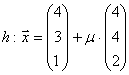
Lösung:
Untersuchung auf Parallelität:
r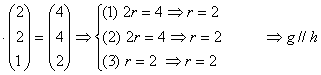
Untersuchung auf Identität:
A(3/2/2) in h:
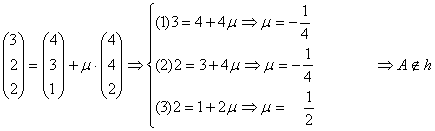
 Der Punkt A(3/2/2) liegt zwar auf der Geraden g, aber nicht auf der Geraden h.
Der Punkt A(3/2/2) liegt zwar auf der Geraden g, aber nicht auf der Geraden h.
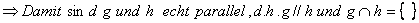
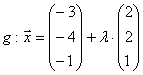 ,
, 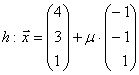
Lösung:
Untersuchung auf Parallelität:
r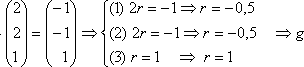 nicht || h
nicht || h
Untersuchung auf gemeinsame Punkte:
Gleichsetzen:
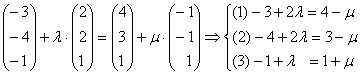
(2)+(3): -5 + 3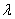 = 4
= 4 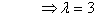
in (3) : -1 + 3 =1 + 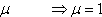
in (1) : -3 + 6 = 4 -1 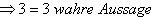
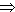 Die Geraden g und h besitzen einen gemeinsamen Punkt S.
Die Geraden g und h besitzen einen gemeinsamen Punkt S.
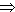 g und h schneiden sich in einem Punkt.
g und h schneiden sich in einem Punkt.
Berechnung des Schnittpunktes S:
 in g einsetzen:
in g einsetzen: 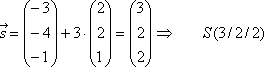
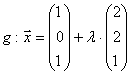 ,
, 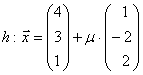
Untersuchung auf Parallelität:
r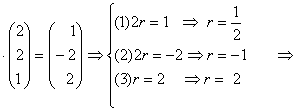 g nicht || h
g nicht || h
Untersuchung auf gemeinsame Punkte:
Gleichsetzen:
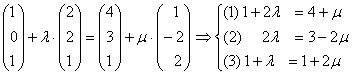
(2) + (3) : 1 + 3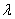 = 4
= 4
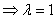

in (2): 2 = 3 -2
= 3 -2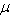
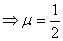
in (1): 1 + 2 = 4 + 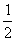
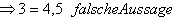
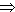 g und h haben keinen gemeinsamen Punkt S.
g und h haben keinen gemeinsamen Punkt S.
 g und h sind windschief.
g und h sind windschief.