2. Inputmatrix (Technologiematrix), Konsumvektor, Produktionsvektor
Eine Verflechtungstabelle ("A-B-C-Matrix") sollte eigentlich nur die Struktur der gegenseitigen
Verflechtung widerspiegeln. An dieser Struktur ändert sich nichts, wenn wir alle Zahlen
in unserem Beispiel etwa verdoppeln oder verzehnfachen oder halbieren.
Um eine eindeutige Darstellung der Verflechtungsstruktur zu erreichen, werden wir alle Zahlen der
Verflechtungstabelle ("A-B-C-Matrix") so umrechnen, dass sie einer Gesamtproduktion
von 1 Einheit entsprechen.
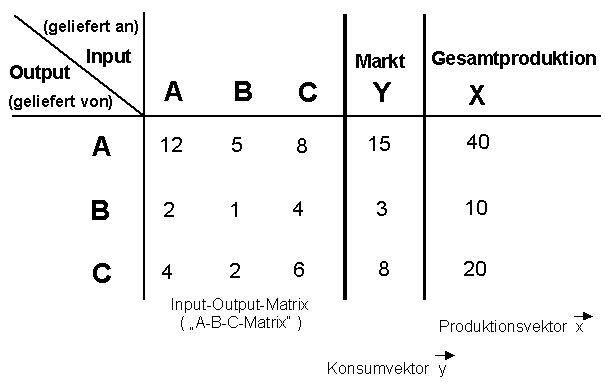 Zur Erinnerung : * In den Zeilen steht der gesamte Output eines Sektors
* In den Spalten steht der gesamte Input eines Sektors
Es gilt : - Sektor A produziert 40 Einheiten und benötigt dazu von sich selbst 12,
von B 2 und von C 4 Einheiten.
Bei der Produktion von 1 Einheit sinkt sein Bedarf an Produktionsmitteln auf den 40. Teil.
Sektor A benötigt dazu also
Zur Erinnerung : * In den Zeilen steht der gesamte Output eines Sektors
* In den Spalten steht der gesamte Input eines Sektors
Es gilt : - Sektor A produziert 40 Einheiten und benötigt dazu von sich selbst 12,
von B 2 und von C 4 Einheiten.
Bei der Produktion von 1 Einheit sinkt sein Bedarf an Produktionsmitteln auf den 40. Teil.
Sektor A benötigt dazu also
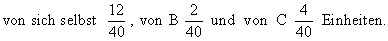 - Analog müssen die Zahlen in der Spalte des Sektors B durch 10 dividiert werden.
- Analog müssen die Zahlen in der Spalte des Sektors C durch 20 dividiert werden.
Unsere Tabelle erhät dann folgendes Aussehen :
- Analog müssen die Zahlen in der Spalte des Sektors B durch 10 dividiert werden.
- Analog müssen die Zahlen in der Spalte des Sektors C durch 20 dividiert werden.
Unsere Tabelle erhät dann folgendes Aussehen :
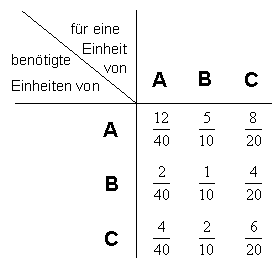 Die Koeffizienten dieser Tabelle heißen Input-Koeffizienten, oder technologische Koeffizienten,
oder Verflechtungskoeffizienten.
Die Matrix, die sie bilden heißt Inputmatrix (oder Technologiematrix).
Sie wird im folgenden stets mit A bezeichnet.
Somit gilt also :
Die Koeffizienten dieser Tabelle heißen Input-Koeffizienten, oder technologische Koeffizienten,
oder Verflechtungskoeffizienten.
Die Matrix, die sie bilden heißt Inputmatrix (oder Technologiematrix).
Sie wird im folgenden stets mit A bezeichnet.
Somit gilt also :
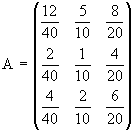 Die Brüche lassen wir ungekürzt stehen, damit der Zusammenhang zwischen der Inputmatrix A,
Die Brüche lassen wir ungekürzt stehen, damit der Zusammenhang zwischen der Inputmatrix A,
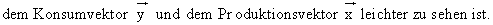
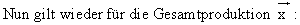
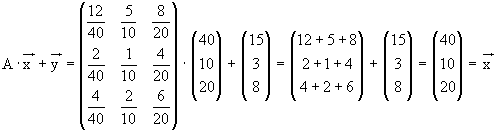 Somit haben wir eine handliche Formel gefunde, die uns den gesuchten Zusammenhang beschreibt :
Somit haben wir eine handliche Formel gefunde, die uns den gesuchten Zusammenhang beschreibt :
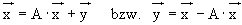
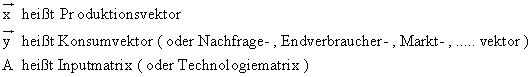 Anmerkungen :
a) Multipliziert man die Inputmatrix A mit dem Produktionsvektor, so erhält man für jeden Sektor
die Gütermenge, die der Sektor produzieren muss, damit alle Sektoren ihre Gesamtproduktion
herstellen können ( gesamter Input ) :
Anmerkungen :
a) Multipliziert man die Inputmatrix A mit dem Produktionsvektor, so erhält man für jeden Sektor
die Gütermenge, die der Sektor produzieren muss, damit alle Sektoren ihre Gesamtproduktion
herstellen können ( gesamter Input ) :
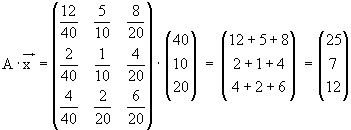 Das heißt :
Zur Produktion von 40 Einheiten im Sektor A , 10 Einheiten im Sektor B und 20 Einheiten
im Sektor C werden insgesamt 25 Einheiten aus Sektor A , 7 Einheiten aus Sektor B und
12 Einheiten aus Sektor C eingesetzt.
b) Die Differenz aus dem Gesamtproduktionsvektor
Das heißt :
Zur Produktion von 40 Einheiten im Sektor A , 10 Einheiten im Sektor B und 20 Einheiten
im Sektor C werden insgesamt 25 Einheiten aus Sektor A , 7 Einheiten aus Sektor B und
12 Einheiten aus Sektor C eingesetzt.
b) Die Differenz aus dem Gesamtproduktionsvektor
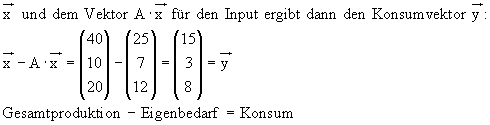 c) Die Inputmatrix (Technologiematrix) hat den Vorteil, dass sie unabhängig vom Konsum und der
Gesamtproduktion ist. Sie bleibt solange unverändert, bis sich die technologischen Gegebenheiten
in der Produktion der Sektoren ändern (siehe Übungsaufgaben, auch mit Parameter).
Deshalb kann mit ihrer Hilfe das Leontief-Modell in der Wirtschaftspolitik dazu benutzt werden,
Prognosen zu erstellen und Entscheidungen zu untermauern.
Denn bei gegebener Inputmatrix (Technologiematrix) A kann einerseits die Frage beantwortet
werden, welche Gütermengen für den Konsumenten bei vorgegebener Gesamtproduktion zur
Verfügung stehen, andererseits lässt sich ermitteln, wieviele Güter produziert werden
müssen, um eine bestimmte Konsumentennachfrage befriedigen zu können
( siehe nächstes Kapitel und Übungsblatt ).
d) Das Leontief-Modell lässt sich auch auf innerbetriebliche Verflechtungen übertragen,bei denen
mehrere Betriebe eines Unternehmens sich gegenseitig und den außerbetrieblichen Markt mit ihren
Produkten beliefern.
e) Die Sektoren werden häufig auch mit S1 , S2 und S3 bezeichnet, oder auch direkt benannt,
wie z.B. Landwirtschaft, Verkehr, Industrie.
f) Konsum- bzw. Produktionsvektor sind ökonomisch nur sinnvoll, wenn sie keine negativen
Komponenten enthalten.
Zu 1. Input-Output-Tabelle , Gozintograph
Zu 3. Aufgabentypen und ihre Lösungen
Zum Übungsblatt
c) Die Inputmatrix (Technologiematrix) hat den Vorteil, dass sie unabhängig vom Konsum und der
Gesamtproduktion ist. Sie bleibt solange unverändert, bis sich die technologischen Gegebenheiten
in der Produktion der Sektoren ändern (siehe Übungsaufgaben, auch mit Parameter).
Deshalb kann mit ihrer Hilfe das Leontief-Modell in der Wirtschaftspolitik dazu benutzt werden,
Prognosen zu erstellen und Entscheidungen zu untermauern.
Denn bei gegebener Inputmatrix (Technologiematrix) A kann einerseits die Frage beantwortet
werden, welche Gütermengen für den Konsumenten bei vorgegebener Gesamtproduktion zur
Verfügung stehen, andererseits lässt sich ermitteln, wieviele Güter produziert werden
müssen, um eine bestimmte Konsumentennachfrage befriedigen zu können
( siehe nächstes Kapitel und Übungsblatt ).
d) Das Leontief-Modell lässt sich auch auf innerbetriebliche Verflechtungen übertragen,bei denen
mehrere Betriebe eines Unternehmens sich gegenseitig und den außerbetrieblichen Markt mit ihren
Produkten beliefern.
e) Die Sektoren werden häufig auch mit S1 , S2 und S3 bezeichnet, oder auch direkt benannt,
wie z.B. Landwirtschaft, Verkehr, Industrie.
f) Konsum- bzw. Produktionsvektor sind ökonomisch nur sinnvoll, wenn sie keine negativen
Komponenten enthalten.
Zu 1. Input-Output-Tabelle , Gozintograph
Zu 3. Aufgabentypen und ihre Lösungen
Zum Übungsblatt
 Zur Erinnerung : * In den Zeilen steht der gesamte Output eines Sektors
* In den Spalten steht der gesamte Input eines Sektors
Es gilt : - Sektor A produziert 40 Einheiten und benötigt dazu von sich selbst 12,
von B 2 und von C 4 Einheiten.
Bei der Produktion von 1 Einheit sinkt sein Bedarf an Produktionsmitteln auf den 40. Teil.
Sektor A benötigt dazu also
Zur Erinnerung : * In den Zeilen steht der gesamte Output eines Sektors
* In den Spalten steht der gesamte Input eines Sektors
Es gilt : - Sektor A produziert 40 Einheiten und benötigt dazu von sich selbst 12,
von B 2 und von C 4 Einheiten.
Bei der Produktion von 1 Einheit sinkt sein Bedarf an Produktionsmitteln auf den 40. Teil.
Sektor A benötigt dazu also
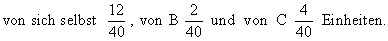 - Analog müssen die Zahlen in der Spalte des Sektors B durch 10 dividiert werden.
- Analog müssen die Zahlen in der Spalte des Sektors C durch 20 dividiert werden.
Unsere Tabelle erhät dann folgendes Aussehen :
- Analog müssen die Zahlen in der Spalte des Sektors B durch 10 dividiert werden.
- Analog müssen die Zahlen in der Spalte des Sektors C durch 20 dividiert werden.
Unsere Tabelle erhät dann folgendes Aussehen :
 Die Koeffizienten dieser Tabelle heißen Input-Koeffizienten, oder technologische Koeffizienten,
oder Verflechtungskoeffizienten.
Die Matrix, die sie bilden heißt Inputmatrix (oder Technologiematrix).
Sie wird im folgenden stets mit A bezeichnet.
Somit gilt also :
Die Koeffizienten dieser Tabelle heißen Input-Koeffizienten, oder technologische Koeffizienten,
oder Verflechtungskoeffizienten.
Die Matrix, die sie bilden heißt Inputmatrix (oder Technologiematrix).
Sie wird im folgenden stets mit A bezeichnet.
Somit gilt also :
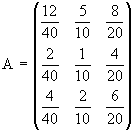 Die Brüche lassen wir ungekürzt stehen, damit der Zusammenhang zwischen der Inputmatrix A,
Die Brüche lassen wir ungekürzt stehen, damit der Zusammenhang zwischen der Inputmatrix A,
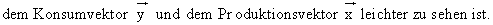
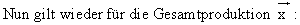
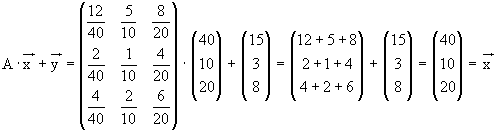 Somit haben wir eine handliche Formel gefunde, die uns den gesuchten Zusammenhang beschreibt :
Somit haben wir eine handliche Formel gefunde, die uns den gesuchten Zusammenhang beschreibt :
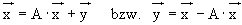
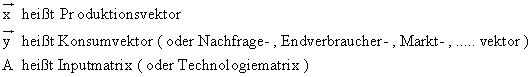 Anmerkungen :
a) Multipliziert man die Inputmatrix A mit dem Produktionsvektor, so erhält man für jeden Sektor
die Gütermenge, die der Sektor produzieren muss, damit alle Sektoren ihre Gesamtproduktion
herstellen können ( gesamter Input ) :
Anmerkungen :
a) Multipliziert man die Inputmatrix A mit dem Produktionsvektor, so erhält man für jeden Sektor
die Gütermenge, die der Sektor produzieren muss, damit alle Sektoren ihre Gesamtproduktion
herstellen können ( gesamter Input ) :
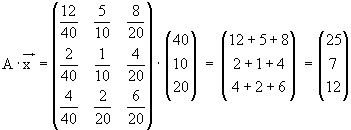 Das heißt :
Zur Produktion von 40 Einheiten im Sektor A , 10 Einheiten im Sektor B und 20 Einheiten
im Sektor C werden insgesamt 25 Einheiten aus Sektor A , 7 Einheiten aus Sektor B und
12 Einheiten aus Sektor C eingesetzt.
b) Die Differenz aus dem Gesamtproduktionsvektor
Das heißt :
Zur Produktion von 40 Einheiten im Sektor A , 10 Einheiten im Sektor B und 20 Einheiten
im Sektor C werden insgesamt 25 Einheiten aus Sektor A , 7 Einheiten aus Sektor B und
12 Einheiten aus Sektor C eingesetzt.
b) Die Differenz aus dem Gesamtproduktionsvektor
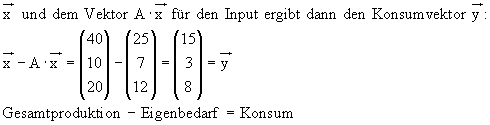 c) Die Inputmatrix (Technologiematrix) hat den Vorteil, dass sie unabhängig vom Konsum und der
Gesamtproduktion ist. Sie bleibt solange unverändert, bis sich die technologischen Gegebenheiten
in der Produktion der Sektoren ändern (siehe Übungsaufgaben, auch mit Parameter).
Deshalb kann mit ihrer Hilfe das Leontief-Modell in der Wirtschaftspolitik dazu benutzt werden,
Prognosen zu erstellen und Entscheidungen zu untermauern.
Denn bei gegebener Inputmatrix (Technologiematrix) A kann einerseits die Frage beantwortet
werden, welche Gütermengen für den Konsumenten bei vorgegebener Gesamtproduktion zur
Verfügung stehen, andererseits lässt sich ermitteln, wieviele Güter produziert werden
müssen, um eine bestimmte Konsumentennachfrage befriedigen zu können
( siehe nächstes Kapitel und Übungsblatt ).
d) Das Leontief-Modell lässt sich auch auf innerbetriebliche Verflechtungen übertragen,bei denen
mehrere Betriebe eines Unternehmens sich gegenseitig und den außerbetrieblichen Markt mit ihren
Produkten beliefern.
e) Die Sektoren werden häufig auch mit S1 , S2 und S3 bezeichnet, oder auch direkt benannt,
wie z.B. Landwirtschaft, Verkehr, Industrie.
f) Konsum- bzw. Produktionsvektor sind ökonomisch nur sinnvoll, wenn sie keine negativen
Komponenten enthalten.
Zu 1. Input-Output-Tabelle , Gozintograph
Zu 3. Aufgabentypen und ihre Lösungen
Zum Übungsblatt
c) Die Inputmatrix (Technologiematrix) hat den Vorteil, dass sie unabhängig vom Konsum und der
Gesamtproduktion ist. Sie bleibt solange unverändert, bis sich die technologischen Gegebenheiten
in der Produktion der Sektoren ändern (siehe Übungsaufgaben, auch mit Parameter).
Deshalb kann mit ihrer Hilfe das Leontief-Modell in der Wirtschaftspolitik dazu benutzt werden,
Prognosen zu erstellen und Entscheidungen zu untermauern.
Denn bei gegebener Inputmatrix (Technologiematrix) A kann einerseits die Frage beantwortet
werden, welche Gütermengen für den Konsumenten bei vorgegebener Gesamtproduktion zur
Verfügung stehen, andererseits lässt sich ermitteln, wieviele Güter produziert werden
müssen, um eine bestimmte Konsumentennachfrage befriedigen zu können
( siehe nächstes Kapitel und Übungsblatt ).
d) Das Leontief-Modell lässt sich auch auf innerbetriebliche Verflechtungen übertragen,bei denen
mehrere Betriebe eines Unternehmens sich gegenseitig und den außerbetrieblichen Markt mit ihren
Produkten beliefern.
e) Die Sektoren werden häufig auch mit S1 , S2 und S3 bezeichnet, oder auch direkt benannt,
wie z.B. Landwirtschaft, Verkehr, Industrie.
f) Konsum- bzw. Produktionsvektor sind ökonomisch nur sinnvoll, wenn sie keine negativen
Komponenten enthalten.
Zu 1. Input-Output-Tabelle , Gozintograph
Zu 3. Aufgabentypen und ihre Lösungen
Zum Übungsblatt