Arbeitsblatt Rationale Funktionen
OStR Starfinger
a) Klärung des Begriffs
Gegeben sind die folgenden Funktionen:
f : x
: x 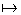
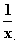 ; f
; f : x
: x 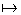
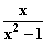 ; f
; f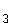 : x
: x 
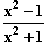 ; f
; f : x
: x 
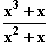 1. Grenzen Sie die genannten Funktionen von Polynomfunktionen ab!
1. Grenzen Sie die genannten Funktionen von Polynomfunktionen ab!  2. In welcher Beziehung stehen die genannten Funktionen zu Polynom-
funktionen?
2. In welcher Beziehung stehen die genannten Funktionen zu Polynom-
funktionen?  3. Definieren Sie nun den Begriff „Rationale Funktion“!
3. Definieren Sie nun den Begriff „Rationale Funktion“!  b) Symmetrie bezüglich des Koordinatensystems
4. Welches Kriterium muss erfüllt sein, damit der Graf einer Funktion
4.1 achsensymmetrisch bzgl. der y-Achse,
4.2 punktsymmetrisch bzgl. des Koordinatenursprungs verläuft?
b) Symmetrie bezüglich des Koordinatensystems
4. Welches Kriterium muss erfüllt sein, damit der Graf einer Funktion
4.1 achsensymmetrisch bzgl. der y-Achse,
4.2 punktsymmetrisch bzgl. des Koordinatenursprungs verläuft?  5. Testen Sie nun die vier eingangs genannten Funktionen auf Symmetrie bzgl. des
Koordinatensystems!
5. Testen Sie nun die vier eingangs genannten Funktionen auf Symmetrie bzgl. des
Koordinatensystems!  6. Stellen Sie eine einfache Regel auf, wie aus dem Symmetrieverhalten des
Zähler- und Nennerpolynoms auf das Symmetrieverhalten der rationalen
Funktion geschlossen werden kann.
6. Stellen Sie eine einfache Regel auf, wie aus dem Symmetrieverhalten des
Zähler- und Nennerpolynoms auf das Symmetrieverhalten der rationalen
Funktion geschlossen werden kann.  7. Formulieren Sie den Umkehrschluss zu der in Aufgabe 6 aufgestellten Regel
und beurteilen Sie dessen Gültigkeit!
7. Formulieren Sie den Umkehrschluss zu der in Aufgabe 6 aufgestellten Regel
und beurteilen Sie dessen Gültigkeit!  c) Definitionsmenge
Dass eine Polynomfunktion wie jede Funktion eine Definitionsmenge besitzt, fällt
allenfalls bei Extremwertaufgaben auf, wo die Definitionsmenge aus praktischen
Gründen eingeschränkt werden muss. Bei rationalen Funktionen hingegen gibt es
für eine Einschränkung der Definitionsmenge mathematische Gründe.
8. Was versteht man unter der Definitionsmenge einer Funktion?
c) Definitionsmenge
Dass eine Polynomfunktion wie jede Funktion eine Definitionsmenge besitzt, fällt
allenfalls bei Extremwertaufgaben auf, wo die Definitionsmenge aus praktischen
Gründen eingeschränkt werden muss. Bei rationalen Funktionen hingegen gibt es
für eine Einschränkung der Definitionsmenge mathematische Gründe.
8. Was versteht man unter der Definitionsmenge einer Funktion?  9. Welchen Grund gibt es bei rationalen Funktionen für die Einschränkung der
Definitionsmenge?
9. Welchen Grund gibt es bei rationalen Funktionen für die Einschränkung der
Definitionsmenge?  10. Bestimmen Sie für i = 1, .. ,4 die Definitionsmengen ID
10. Bestimmen Sie für i = 1, .. ,4 die Definitionsmengen ID der in a) genannten
Funktionen f
der in a) genannten
Funktionen f !
!  d) Verhalten der rationalen Funktion an den Definitionslücken
11. f
d) Verhalten der rationalen Funktion an den Definitionslücken
11. f : x
: x 
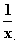 11.1 Wählen Sie für x die Zahlenfolge
11.1 Wählen Sie für x die Zahlenfolge 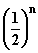 , n = 1; 2; 3; . . . , und beobachten
Sie, wie sich die Funktionswerte verhalten!
11.2 Führen Sie die gleiche Untersuchung für x < 0 durch!
Die in 11.1 und 11.2 gewonnene Erkenntnis lässt sich formal folgendermaßen
wiedergeben:
x
, n = 1; 2; 3; . . . , und beobachten
Sie, wie sich die Funktionswerte verhalten!
11.2 Führen Sie die gleiche Untersuchung für x < 0 durch!
Die in 11.1 und 11.2 gewonnene Erkenntnis lässt sich formal folgendermaßen
wiedergeben:
x 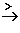 0
0  f
f (x)
(x)  +∞
x
+∞
x 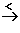 0
0  f
f (x)
(x)  –∞
oder kurz: x
–∞
oder kurz: x 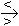 0
0  f
f (x)
(x) 
 ∞
Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen ∞
oder gegen –∞ streben, heißt „Polstelle“ oder „Unendlichkeitsstelle“.
Im Beispiel handelt es sich um eine Polstelle „mit Vorzeichenwechsel“.
11.3 Durch welche einfache Abwandlung des Funktionsterms von f
∞
Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen ∞
oder gegen –∞ streben, heißt „Polstelle“ oder „Unendlichkeitsstelle“.
Im Beispiel handelt es sich um eine Polstelle „mit Vorzeichenwechsel“.
11.3 Durch welche einfache Abwandlung des Funktionsterms von f liegt bei
x = 0 eine Polstelle ohne Vorzeichenwechsel vor?
liegt bei
x = 0 eine Polstelle ohne Vorzeichenwechsel vor?  12. f
12. f : x
: x 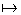
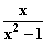 12.1 Wählen Sie Zahlenfolgen, die von links bzw von rechts gegen die jeweilige
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
Die beiden Definitionslücken sind also Polstellen mit Vorzeichenwechsel.
Zu dieser experimentellen Möglichkeit, das Verhalten der rationalen Funktion
an ihren Definitionslücken zu ermitteln, gibt es eine elegante Alternative:
Zunächst macht man sich das Verhalten des Nenners an einer Skizze klar:
12.1 Wählen Sie Zahlenfolgen, die von links bzw von rechts gegen die jeweilige
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
Die beiden Definitionslücken sind also Polstellen mit Vorzeichenwechsel.
Zu dieser experimentellen Möglichkeit, das Verhalten der rationalen Funktion
an ihren Definitionslücken zu ermitteln, gibt es eine elegante Alternative:
Zunächst macht man sich das Verhalten des Nenners an einer Skizze klar:
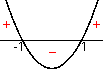
Dann folgt:
x 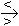 –1
–1  f
f (x) =
(x) = 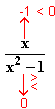

 ∞; x
∞; x 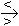 1
1  f
f (x) =
(x) = 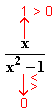

 ∞
Wegen der Punktsymmetrie des Grafen von f
∞
Wegen der Punktsymmetrie des Grafen von f folgt das Verhalten von f
folgt das Verhalten von f an der
rechten Definitionslücke auch aus seinem Verhalten an der linken Definitions-
lücke.
Es gibt auch eine tabellarische Darstellungsmöglichkeit für den Sachverhalt:
an der
rechten Definitionslücke auch aus seinem Verhalten an der linken Definitions-
lücke.
Es gibt auch eine tabellarische Darstellungsmöglichkeit für den Sachverhalt:
| | x < | –1 | < x < | 0 | < x < | 1 | < x |
|---|
Zähler von f | – | – | – | 0 | + | + | + |
Nenner von f | + | 0 | – | – | – | 0 | + |
f (x) (x) | –  | –∞ / +∞ | 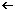 + + | 0 | –  | –∞ / +∞ | 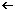 + + |
12.2 Durch welche einfache Abwandlung des Funktionsterms von f liegen bei
x = –1 und x = 1 Polstellen ohne Vorzeichenwechsel vor?
liegen bei
x = –1 und x = 1 Polstellen ohne Vorzeichenwechsel vor?  13. f
13. f : x
: x 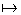
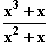 13.1 Untersuchen Sie das Verhalten von f
13.1 Untersuchen Sie das Verhalten von f an ihrer linken Definitionslücke!
an ihrer linken Definitionslücke!
 13.2 Wählen Sie Zahlenfolgen, die von links bzw. von rechts gegen die rechte
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
An der Definitionslücke x = 0 streben die Funktionswerte von f
13.2 Wählen Sie Zahlenfolgen, die von links bzw. von rechts gegen die rechte
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
An der Definitionslücke x = 0 streben die Funktionswerte von f offenbar
nicht gegen ∞ oder gegen –∞, sondern augenscheinlich gegen den Wert y = 1.
Dieses überraschende Verhalten hängt damit zusammen, dass man den
Funktionsterm von f
offenbar
nicht gegen ∞ oder gegen –∞, sondern augenscheinlich gegen den Wert y = 1.
Dieses überraschende Verhalten hängt damit zusammen, dass man den
Funktionsterm von f um den Faktor x kürzen kann, und der gekürzte Term
bei x = 0 plötzlich definiert ist.
13.3 Führen Sie diesen Kürzvorgang durch, und untersuchen Sie das Verhalten
der Funktion f
um den Faktor x kürzen kann, und der gekürzte Term
bei x = 0 plötzlich definiert ist.
13.3 Führen Sie diesen Kürzvorgang durch, und untersuchen Sie das Verhalten
der Funktion f bei x = 0 an ihrem gekürzten Term!
bei x = 0 an ihrem gekürzten Term!  Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen
einen endlichen Wert streben, heißt „stetig behebbare Lücke“ oder kurz
„hebbare Lücke“.
Dieser Begriff kommt daher, dass der gekürzte Term die besagte Lücke nicht
mehr besitzt, sie also „stetig behoben“ ist. Der gekürzte Term heißt deshalb
„stetige Fortsetzung“ der ungekürzten rationalen Funktion. Da die Definitions-
menge der stetigen Fortsetzung mit der Definitionsmenge der ursprünglichen
Funktion nicht mehr übereinstimmt, handelt es sich bei der stetigen Fortsetzung
um eine neue Funktion, deren Symbol aus dem der ursprünglichen Funktion
durch Hinzufügung einer Tilde (=Schlange) oder eines Sterns entlehnt wird (also
Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen
einen endlichen Wert streben, heißt „stetig behebbare Lücke“ oder kurz
„hebbare Lücke“.
Dieser Begriff kommt daher, dass der gekürzte Term die besagte Lücke nicht
mehr besitzt, sie also „stetig behoben“ ist. Der gekürzte Term heißt deshalb
„stetige Fortsetzung“ der ungekürzten rationalen Funktion. Da die Definitions-
menge der stetigen Fortsetzung mit der Definitionsmenge der ursprünglichen
Funktion nicht mehr übereinstimmt, handelt es sich bei der stetigen Fortsetzung
um eine neue Funktion, deren Symbol aus dem der ursprünglichen Funktion
durch Hinzufügung einer Tilde (=Schlange) oder eines Sterns entlehnt wird (also
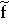 oder
oder 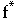 ), um so die Verwandtschaft beider Funktionen zu dokumentieren.
), um so die Verwandtschaft beider Funktionen zu dokumentieren.
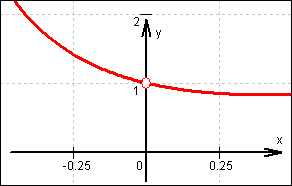
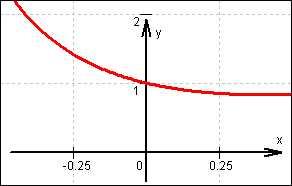 Graf von f
Graf von f bei x = 0 Graf von
bei x = 0 Graf von 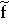
 bei x = 0
Ist die gemeinsame Nullstelle von Zähler und Nenner nicht x = 0, so muss vor
dem Kürzen der rationalen Funktion in der Regel noch eine Polynomdivision des
Zählers und des Nenners durchgeführt werden, um sie in Faktoren zerlegen zu
können.
e) Nullstellen
14. Wann hat ein Bruch den Wert null?
bei x = 0
Ist die gemeinsame Nullstelle von Zähler und Nenner nicht x = 0, so muss vor
dem Kürzen der rationalen Funktion in der Regel noch eine Polynomdivision des
Zählers und des Nenners durchgeführt werden, um sie in Faktoren zerlegen zu
können.
e) Nullstellen
14. Wann hat ein Bruch den Wert null?  15. Bestiimmen Sie die Nullstellen der Funkionen f
15. Bestiimmen Sie die Nullstellen der Funkionen f bis f
bis f von a)!
von a)!  Bearbeiten Sie nun vom Übungsblatt die Aufgaben 1, 3 a) und 4 a)!
f) Asymptoten
Unter der „Asymptote“ eines Funktionsgrafen versteht man eine Gerade oder
Kurve (in diesem Fall auch „asymptotische Kurve“ genannt), an die sich in
einem gewissen Bereich der Funktionsgraf beliebig nah anschmiegt, sie aber
nicht erreicht.
16. Skizzieren Sie an Hand geeigneter Wertetabellen die Grafen der Funktionen
f
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 1, 3 a) und 4 a)!
f) Asymptoten
Unter der „Asymptote“ eines Funktionsgrafen versteht man eine Gerade oder
Kurve (in diesem Fall auch „asymptotische Kurve“ genannt), an die sich in
einem gewissen Bereich der Funktionsgraf beliebig nah anschmiegt, sie aber
nicht erreicht.
16. Skizzieren Sie an Hand geeigneter Wertetabellen die Grafen der Funktionen
f bis f
bis f von a), und geben Sie dann die Gleichungen aller Asymptoten an!
von a), und geben Sie dann die Gleichungen aller Asymptoten an!
 Aus dieser Aufgabe wird sofort klar, dass die Polstellen einer rationalen
Funktion direkt zu den Gleichungen der senkrechten Asymptoten führen.
Im Folgenden wird der Grad des Zähler- bzw. Nennerpolynoms kurz als
„Zählergrad“ bzw. „Nennergrad“ bezeichnet.
17. Welche nicht senkrechte Asymptote muss eine rationale Funktion haben,
deren Zählergrad kleiner ist als ihr Nennergrad? Begründung!
Aus dieser Aufgabe wird sofort klar, dass die Polstellen einer rationalen
Funktion direkt zu den Gleichungen der senkrechten Asymptoten führen.
Im Folgenden wird der Grad des Zähler- bzw. Nennerpolynoms kurz als
„Zählergrad“ bzw. „Nennergrad“ bezeichnet.
17. Welche nicht senkrechte Asymptote muss eine rationale Funktion haben,
deren Zählergrad kleiner ist als ihr Nennergrad? Begründung!  18. f
18. f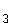 : x
: x 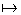
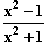 18.1 Führen Sie die Polynomdivision Zählerpolynom : Nennerpolynom durch,
und stellen Sie den Divisionsrest analog zum schriftlichen Dividieren als
„echt gebrochen-rationale Funktion“ (d. h. Zählergrad < Nennergrad)
in den Quotienten.
18.1 Führen Sie die Polynomdivision Zählerpolynom : Nennerpolynom durch,
und stellen Sie den Divisionsrest analog zum schriftlichen Dividieren als
„echt gebrochen-rationale Funktion“ (d. h. Zählergrad < Nennergrad)
in den Quotienten.  18.2 Überzeugen Sie sich durch Umwandlung des Quotienten von 18.1 in einen
geschlossenen Bruch, dass der Quotient nur eine andere Form der Aus-
gangsfunktion darstellt.
18.2 Überzeugen Sie sich durch Umwandlung des Quotienten von 18.1 in einen
geschlossenen Bruch, dass der Quotient nur eine andere Form der Aus-
gangsfunktion darstellt.  Sie sehen, dass die rationale Funktion f
Sie sehen, dass die rationale Funktion f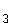 einen „ganz-rationalen Anteil“ (nämlich
„ 1 “) und einen „echt gebrochen-rationalen Anteil“ (nämlich
einen „ganz-rationalen Anteil“ (nämlich
„ 1 “) und einen „echt gebrochen-rationalen Anteil“ (nämlich 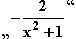 ) besitzt.
18.3 Untersuchen Sie das Verhalten der zerlegten Form von f
) besitzt.
18.3 Untersuchen Sie das Verhalten der zerlegten Form von f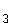 für x
für x  ± ∞!
± ∞!
 Damit hat sich der empirische Befund, dass der Graf von f
Damit hat sich der empirische Befund, dass der Graf von f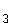 die waagrechte
Asymptote y = 1 besitzt, rechnerisch bestätigt.
19. Ermitteln Sie auf dem gleichen Wege rechnerisch die Gleichung der nicht
senkrechten Asymptote des Grafen von f
die waagrechte
Asymptote y = 1 besitzt, rechnerisch bestätigt.
19. Ermitteln Sie auf dem gleichen Wege rechnerisch die Gleichung der nicht
senkrechten Asymptote des Grafen von f !
!  Im Fall Zählergrad ≥ Nennergrad gilt also:
Der Funktionsterm für die nicht senkrechte Asymptote des Grafen einer rationalen
Funktion ist gleich ihrem ganz-rationalen Anteil.
20. Welcher Zusammenhang besteht zwischen dem Zählergrad, dem Nennergrad
und dem Grad der nicht senkrechten Asymptote?
Im Fall Zählergrad ≥ Nennergrad gilt also:
Der Funktionsterm für die nicht senkrechte Asymptote des Grafen einer rationalen
Funktion ist gleich ihrem ganz-rationalen Anteil.
20. Welcher Zusammenhang besteht zwischen dem Zählergrad, dem Nennergrad
und dem Grad der nicht senkrechten Asymptote?  Bearbeiten Sie nun vom Übungsblatt die Aufgaben 2 a) und b) !
g) Monotonie und Krümmung
Zum Ableiten einer rationalen Funktion benötigt man die „Quotientenregel“.
Um diese herzuleiten, sind einige Ableitungsregeln nötig:
• Produktregel: (f(x) · g(x))' = f '(x) · g(x) + f(x) · g'(x) Beweis
„Die Ableitung des Produktes zweier differenzierbarer
Funktionen ist gleich der Summe der Produkte jeweils
einer abgeleiteten und einer belassenen Funktion.“
• Kettenregel: f(g(x))' = f '(g(x)) · g'(x) Beweis
„Die Ableitung einer verketteten Funktion ist gleich dem
Produkt der abgeleiteten äußeren Funktion bei belassener
innerer Funktion und der abgeleiteten inneren Funktion.“
• Ableitung von f(x) =
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 2 a) und b) !
g) Monotonie und Krümmung
Zum Ableiten einer rationalen Funktion benötigt man die „Quotientenregel“.
Um diese herzuleiten, sind einige Ableitungsregeln nötig:
• Produktregel: (f(x) · g(x))' = f '(x) · g(x) + f(x) · g'(x) Beweis
„Die Ableitung des Produktes zweier differenzierbarer
Funktionen ist gleich der Summe der Produkte jeweils
einer abgeleiteten und einer belassenen Funktion.“
• Kettenregel: f(g(x))' = f '(g(x)) · g'(x) Beweis
„Die Ableitung einer verketteten Funktion ist gleich dem
Produkt der abgeleiteten äußeren Funktion bei belassener
innerer Funktion und der abgeleiteten inneren Funktion.“
• Ableitung von f(x) = 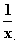 : f '(x) =
: f '(x) = 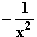 Beweis
21. Überzeugen Sie sich am Beispiel f(x) = x
Beweis
21. Überzeugen Sie sich am Beispiel f(x) = x und g(x) = x
und g(x) = x + 1 von der
Gültigkeit der Produktregel!
+ 1 von der
Gültigkeit der Produktregel!  22. Zeigen Sie am Beispiel f(x) = (x
22. Zeigen Sie am Beispiel f(x) = (x – x)
– x) die Gültigkeit der Kettenregel auf!
die Gültigkeit der Kettenregel auf!
 23. Zeigen Sie mit Hilfe der zwei letzten aufgeführten Regeln, dass die Ableitungs-
regel
23. Zeigen Sie mit Hilfe der zwei letzten aufgeführten Regeln, dass die Ableitungs-
regel 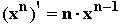 , n
, n 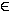 IN, auf n
IN, auf n 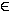
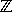 \{0} ausgedehnt werden kann.
Leiten Sie sodann die folgenden Funktionen ab:
a) f(x) =
\{0} ausgedehnt werden kann.
Leiten Sie sodann die folgenden Funktionen ab:
a) f(x) = 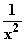 b) f(x) =
b) f(x) = 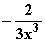 c) f(x) =
c) f(x) = 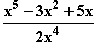
 24. Eine rationale Funktion kann in der Form
24. Eine rationale Funktion kann in der Form 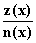 =
= 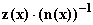 dargestellt
werden. Leiten Sie anhand dieser Darstellung mit Hilfe der aufgeführten
Regeln die „Quotientenregel“ zur Ableitung einer rationalen Funktion her!
dargestellt
werden. Leiten Sie anhand dieser Darstellung mit Hilfe der aufgeführten
Regeln die „Quotientenregel“ zur Ableitung einer rationalen Funktion her!
 • Quotientenregel: (
• Quotientenregel: (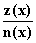 )' =
)' =  Beweis
„Die Ableitung einer rationalen Funktion ist gleich dem
Quotienten aus Nenner mal Ableitung des Zählers minus
Zähler mal Ableitung des Nenners und dem Nennerquadrat.“
kurz:
Beweis
„Die Ableitung einer rationalen Funktion ist gleich dem
Quotienten aus Nenner mal Ableitung des Zählers minus
Zähler mal Ableitung des Nenners und dem Nennerquadrat.“
kurz: 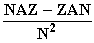 25.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Monotonie-
verhalten?
25.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Monotonie-
verhalten?  25.2 An welchen Stellen ändert sich bei einer rationalen Funktion das Monotonie-
verhalten?
25.2 An welchen Stellen ändert sich bei einer rationalen Funktion das Monotonie-
verhalten?  25.3 Geben Sie die Gleichung einer möglichst einfachen rationalen Funktion an,
bei der sich das Monotonieverhalten ändert, ohne dass eine Extremstelle
vorliegt. Geben Sie auch an, in welchem Bereich die Funktion steigt bzw.
fällt.
25.3 Geben Sie die Gleichung einer möglichst einfachen rationalen Funktion an,
bei der sich das Monotonieverhalten ändert, ohne dass eine Extremstelle
vorliegt. Geben Sie auch an, in welchem Bereich die Funktion steigt bzw.
fällt.  26.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Krümmungs-
verhalten?
26.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Krümmungs-
verhalten?  26.2 An welchen Stellen ändert sich bei einer rationalen Funktion das
Krümmungsverhalten?
26.2 An welchen Stellen ändert sich bei einer rationalen Funktion das
Krümmungsverhalten?  26.3 Geben Sie die Gleichung einer möglichst einfachen rationalen Funktion an,
bei der sich das Krümmungsverhalten ändert, ohne dass eine Wendestelle
vorliegt. Geben Sie auch an, in welchem Bereich der Graf der Funktion
links- bzw. rechtsgekrümmt ist.
26.3 Geben Sie die Gleichung einer möglichst einfachen rationalen Funktion an,
bei der sich das Krümmungsverhalten ändert, ohne dass eine Wendestelle
vorliegt. Geben Sie auch an, in welchem Bereich der Graf der Funktion
links- bzw. rechtsgekrümmt ist.  Sie sehen also, dass Sie bei der Monotonie- bzw. Krümmungsuntersuchung einer
rationalen Funktion nicht nur die Nullstellen der ersten bzw. zweiten Ableitung,
sondern auch die Definitionslücken auflisten müssen.
27.1 Gegeben ist eine rationale Funktion, deren Nenner ein Quadrat darstellt.
Zeigen Sie allgemein, dass dann der Nenner der Ableitungsfunktion eine
dritte Potenz darstellt.
Sie sehen also, dass Sie bei der Monotonie- bzw. Krümmungsuntersuchung einer
rationalen Funktion nicht nur die Nullstellen der ersten bzw. zweiten Ableitung,
sondern auch die Definitionslücken auflisten müssen.
27.1 Gegeben ist eine rationale Funktion, deren Nenner ein Quadrat darstellt.
Zeigen Sie allgemein, dass dann der Nenner der Ableitungsfunktion eine
dritte Potenz darstellt.  27.2 Gegeben ist eine rationale Funktion, deren Nenner eine i-te Potenz darstellt
(i
27.2 Gegeben ist eine rationale Funktion, deren Nenner eine i-te Potenz darstellt
(i 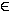 IN). Zeigen Sie allgemein, dass dann der Nenner der Ableitungsfunktion
eine (i + 1)–te Potenz darstellt.
IN). Zeigen Sie allgemein, dass dann der Nenner der Ableitungsfunktion
eine (i + 1)–te Potenz darstellt.  Wenn der Nenner der rationalen Funktion ein Quadrat oder eine höhere Potenz
darstellt, ist also, wie Sie sehen, der Term der Ableitungsfunktion stets kürzbar.
Denken Sie immer an diese Kürzmöglichkeit, denn sonst bläht sich der Ab-
leitungsterm unnötig auf, und die Nullstellenbestimmung wird viel schwieriger.
Im Übrigen werden Monotonie und Krümmung bei rationalen Funktionen genau
so untersucht wie bei Polynomfunktionen. Bei der tabellarischen Untersuchung
sollten vor der Vorzeichenbilanz der entsprechenden Ableitungsfunktion die Vor-
zeichen ihres Zählers und Nenners aufgelistet werden.
28. Untersuchen Sie das Monotonieverhalten der Funktionen f
Wenn der Nenner der rationalen Funktion ein Quadrat oder eine höhere Potenz
darstellt, ist also, wie Sie sehen, der Term der Ableitungsfunktion stets kürzbar.
Denken Sie immer an diese Kürzmöglichkeit, denn sonst bläht sich der Ab-
leitungsterm unnötig auf, und die Nullstellenbestimmung wird viel schwieriger.
Im Übrigen werden Monotonie und Krümmung bei rationalen Funktionen genau
so untersucht wie bei Polynomfunktionen. Bei der tabellarischen Untersuchung
sollten vor der Vorzeichenbilanz der entsprechenden Ableitungsfunktion die Vor-
zeichen ihres Zählers und Nenners aufgelistet werden.
28. Untersuchen Sie das Monotonieverhalten der Funktionen f bis f
bis f von a),
und geben Sie gegebenenfalls auch die Art und die Koordinaten der Extrem-
punkte an!
von a),
und geben Sie gegebenenfalls auch die Art und die Koordinaten der Extrem-
punkte an!  29. Untersuchen Sie das Krümmungsverhalten der Funktionen f
29. Untersuchen Sie das Krümmungsverhalten der Funktionen f bis f
bis f von a,
und geben Sie gegebenenfalls auch die Koordinaten der Wendepunkte an!
von a,
und geben Sie gegebenenfalls auch die Koordinaten der Wendepunkte an!
 Bearbeiten Sie nun vom Übungsblatt die Aufgaben 2 c) und d), 3 a)–d), 4 a)–d),
5 a)–d) sowie 6 a)–c) !
h) Integration
30. Sie haben gesehen, dass die Ableitungsregel
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 2 c) und d), 3 a)–d), 4 a)–d),
5 a)–d) sowie 6 a)–c) !
h) Integration
30. Sie haben gesehen, dass die Ableitungsregel 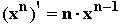 für n
für n 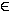
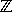 \{0}
gilt. Wie lautet dann die umgekehrte Regel für die Integration von xn und in
welchem Zahlenbereich für n ist sie gültig?
\{0}
gilt. Wie lautet dann die umgekehrte Regel für die Integration von xn und in
welchem Zahlenbereich für n ist sie gültig?  31. Geben Sie jeweils die Menge aller Stammfunktionen an:
a) f(x) =
31. Geben Sie jeweils die Menge aller Stammfunktionen an:
a) f(x) = 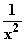 b) f(x) =
b) f(x) = 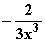 c) f(x) =
c) f(x) = 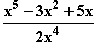
 32. Gegeben ist die Funktion f: x
32. Gegeben ist die Funktion f: x 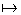
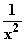 mit ID
mit ID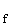 = IR \ {0}.
32.1 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = 2 einschließt. Fertigen Sie eine Skizze
und kennzeichnen Sie die berechnete Fläche!
= IR \ {0}.
32.1 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = 2 einschließt. Fertigen Sie eine Skizze
und kennzeichnen Sie die berechnete Fläche!  32.2 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = c (c > 1) einschließt.
32.2 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = c (c > 1) einschließt.  32.3 Gegen welchen Wert strebt die Flächenmaßzahl von 32.2 für c
32.3 Gegen welchen Wert strebt die Flächenmaßzahl von 32.2 für c  ∞ ?
Deuten Sie diesen Grenzwert geometrisch und veranschaulichen Sie Ihre
Deutung grafisch!
∞ ?
Deuten Sie diesen Grenzwert geometrisch und veranschaulichen Sie Ihre
Deutung grafisch!  Der Grenzwert von
Der Grenzwert von 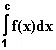 für c
für c  ∞ wird auch als
∞ wird auch als 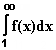 dargestellt und als
„uneigentliches Integral“ von f bezeichnet, da nicht beide Integrationsgrenzen
endlich sind.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 e), 4 e)–g), 5 e) und f)
sowie 6 d)–f) !
Bearbeiten Sie nun die restlichen Aufgaben 7 bis 11 des Übungsblattes!
dargestellt und als
„uneigentliches Integral“ von f bezeichnet, da nicht beide Integrationsgrenzen
endlich sind.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 e), 4 e)–g), 5 e) und f)
sowie 6 d)–f) !
Bearbeiten Sie nun die restlichen Aufgaben 7 bis 11 des Übungsblattes!
 : x
: x 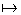
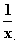 ; f
; f : x
: x 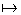
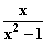 ; f
; f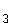 : x
: x 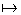
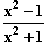 ; f
; f : x
: x 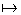
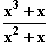 1. Grenzen Sie die genannten Funktionen von Polynomfunktionen ab!
1. Grenzen Sie die genannten Funktionen von Polynomfunktionen ab!  der in a) genannten
Funktionen f
der in a) genannten
Funktionen f !
!  : x
: x 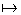
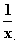 11.1 Wählen Sie für x die Zahlenfolge
11.1 Wählen Sie für x die Zahlenfolge 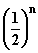 , n = 1; 2; 3; . . . , und beobachten
Sie, wie sich die Funktionswerte verhalten!
11.2 Führen Sie die gleiche Untersuchung für x < 0 durch!
Die in 11.1 und 11.2 gewonnene Erkenntnis lässt sich formal folgendermaßen
wiedergeben:
x
, n = 1; 2; 3; . . . , und beobachten
Sie, wie sich die Funktionswerte verhalten!
11.2 Führen Sie die gleiche Untersuchung für x < 0 durch!
Die in 11.1 und 11.2 gewonnene Erkenntnis lässt sich formal folgendermaßen
wiedergeben:
x  0
0  f
f (x)
(x)  +∞
x
+∞
x 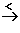 0
0  f
f (x)
(x)  –∞
oder kurz: x
–∞
oder kurz: x 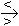 0
0  f
f (x)
(x) 
 ∞
Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen ∞
oder gegen –∞ streben, heißt „Polstelle“ oder „Unendlichkeitsstelle“.
Im Beispiel handelt es sich um eine Polstelle „mit Vorzeichenwechsel“.
11.3 Durch welche einfache Abwandlung des Funktionsterms von f
∞
Eine solche Definitionslücke, in deren Umgebung die Funktionswerte gegen ∞
oder gegen –∞ streben, heißt „Polstelle“ oder „Unendlichkeitsstelle“.
Im Beispiel handelt es sich um eine Polstelle „mit Vorzeichenwechsel“.
11.3 Durch welche einfache Abwandlung des Funktionsterms von f liegt bei
x = 0 eine Polstelle ohne Vorzeichenwechsel vor?
liegt bei
x = 0 eine Polstelle ohne Vorzeichenwechsel vor?  : x
: x 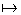
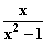 12.1 Wählen Sie Zahlenfolgen, die von links bzw von rechts gegen die jeweilige
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
Die beiden Definitionslücken sind also Polstellen mit Vorzeichenwechsel.
Zu dieser experimentellen Möglichkeit, das Verhalten der rationalen Funktion
an ihren Definitionslücken zu ermitteln, gibt es eine elegante Alternative:
Zunächst macht man sich das Verhalten des Nenners an einer Skizze klar:
12.1 Wählen Sie Zahlenfolgen, die von links bzw von rechts gegen die jeweilige
Definitionslücke streben, und ermitteln Sie mit Hilfe des Taschenrechners,
wie sich die Funktionswerte verhalten!
Die beiden Definitionslücken sind also Polstellen mit Vorzeichenwechsel.
Zu dieser experimentellen Möglichkeit, das Verhalten der rationalen Funktion
an ihren Definitionslücken zu ermitteln, gibt es eine elegante Alternative:
Zunächst macht man sich das Verhalten des Nenners an einer Skizze klar:

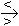 –1
–1  f
f (x) =
(x) = 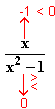

 ∞; x
∞; x 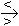 1
1  f
f (x) =
(x) = 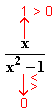

 ∞
Wegen der Punktsymmetrie des Grafen von f
∞
Wegen der Punktsymmetrie des Grafen von f folgt das Verhalten von f
folgt das Verhalten von f an der
rechten Definitionslücke auch aus seinem Verhalten an der linken Definitions-
lücke.
Es gibt auch eine tabellarische Darstellungsmöglichkeit für den Sachverhalt:
an der
rechten Definitionslücke auch aus seinem Verhalten an der linken Definitions-
lücke.
Es gibt auch eine tabellarische Darstellungsmöglichkeit für den Sachverhalt: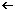 +
+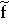 oder
oder 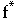 ), um so die Verwandtschaft beider Funktionen zu dokumentieren.
), um so die Verwandtschaft beider Funktionen zu dokumentieren.

 Graf von f
Graf von f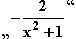 ) besitzt.
18.3 Untersuchen Sie das Verhalten der zerlegten Form von f
) besitzt.
18.3 Untersuchen Sie das Verhalten der zerlegten Form von f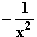 Beweis
21. Überzeugen Sie sich am Beispiel f(x) = x
Beweis
21. Überzeugen Sie sich am Beispiel f(x) = x und g(x) = x
und g(x) = x + 1 von der
Gültigkeit der Produktregel!
+ 1 von der
Gültigkeit der Produktregel! 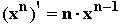 , n
, n 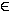 IN, auf n
IN, auf n  \{0} ausgedehnt werden kann.
Leiten Sie sodann die folgenden Funktionen ab:
a) f(x) =
\{0} ausgedehnt werden kann.
Leiten Sie sodann die folgenden Funktionen ab:
a) f(x) = 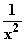 b) f(x) =
b) f(x) = 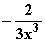 c) f(x) =
c) f(x) = 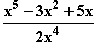
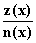 =
= 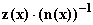 dargestellt
werden. Leiten Sie anhand dieser Darstellung mit Hilfe der aufgeführten
Regeln die „Quotientenregel“ zur Ableitung einer rationalen Funktion her!
dargestellt
werden. Leiten Sie anhand dieser Darstellung mit Hilfe der aufgeführten
Regeln die „Quotientenregel“ zur Ableitung einer rationalen Funktion her!
 Beweis
„Die Ableitung einer rationalen Funktion ist gleich dem
Quotienten aus Nenner mal Ableitung des Zählers minus
Zähler mal Ableitung des Nenners und dem Nennerquadrat.“
kurz:
Beweis
„Die Ableitung einer rationalen Funktion ist gleich dem
Quotienten aus Nenner mal Ableitung des Zählers minus
Zähler mal Ableitung des Nenners und dem Nennerquadrat.“
kurz: 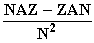 25.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Monotonie-
verhalten?
25.1 An welchen Stellen ändert sich bei einer Polynomfunktion das Monotonie-
verhalten? 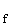 = IR \ {0}.
32.1 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = 2 einschließt. Fertigen Sie eine Skizze
und kennzeichnen Sie die berechnete Fläche!
= IR \ {0}.
32.1 Berechnen Sie die Maßzahl der Fläche, die der Graf von f mit der x-Achse
und den Geraden x = 1 und x = 2 einschließt. Fertigen Sie eine Skizze
und kennzeichnen Sie die berechnete Fläche! 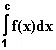 für c
für c 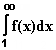 dargestellt und als
„uneigentliches Integral“ von f bezeichnet, da nicht beide Integrationsgrenzen
endlich sind.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 e), 4 e)–g), 5 e) und f)
sowie 6 d)–f) !
Bearbeiten Sie nun die restlichen Aufgaben 7 bis 11 des Übungsblattes!
dargestellt und als
„uneigentliches Integral“ von f bezeichnet, da nicht beide Integrationsgrenzen
endlich sind.
Bearbeiten Sie nun vom Übungsblatt die Aufgaben 3 e), 4 e)–g), 5 e) und f)
sowie 6 d)–f) !
Bearbeiten Sie nun die restlichen Aufgaben 7 bis 11 des Übungsblattes!