1. Gegeben sind die Funktionen
f : x
: x 
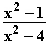 , f
, f : x
: x 
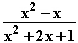 ,
f
,
f : x
: x 
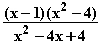 , f
, f : x
: x 
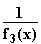 mit jeweils maximaler reeller Definitionsmenge.
a) Bestimmen Sie jeweils die Definitionslücken und die Nullstellen.
b) Welches Verhalten zeigt die jeweilige Funktion in der Umgebung ihrer
Definitionslücken?
mit jeweils maximaler reeller Definitionsmenge.
a) Bestimmen Sie jeweils die Definitionslücken und die Nullstellen.
b) Welches Verhalten zeigt die jeweilige Funktion in der Umgebung ihrer
Definitionslücken? 2. Gegeben sind die Funktionen
f
2. Gegeben sind die Funktionen
f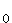 : x
: x 
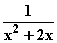 und f
und f : x
: x 
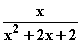 mit jeweils max. Definitionsmenge
sowie f
mit jeweils max. Definitionsmenge
sowie f , f
, f und f
und f aus Aufgabe 1.
a) Bestimmen Sie jeweils die Gleichungen der Asymptoten.
b) Wo verläuft der Graf der jeweiligen Funktion oberhalb, wo unterhalb
seiner nichtsenkrechten Asymptote?
c) Untersuchen Sie das Monotonieverhalten der jeweiligen Funktionen, und
geben Sie ggf. die Art und die Koordinaten der Extrempunkte an.
d) Fertigen Sie Skizzen der jeweiligen Grafen.
aus Aufgabe 1.
a) Bestimmen Sie jeweils die Gleichungen der Asymptoten.
b) Wo verläuft der Graf der jeweiligen Funktion oberhalb, wo unterhalb
seiner nichtsenkrechten Asymptote?
c) Untersuchen Sie das Monotonieverhalten der jeweiligen Funktionen, und
geben Sie ggf. die Art und die Koordinaten der Extrempunkte an.
d) Fertigen Sie Skizzen der jeweiligen Grafen. 3. Gegeben ist die Funktion f : x
3. Gegeben ist die Funktion f : x 
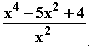 mit ID
mit ID = IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten und die Nullstellen von f und
untersuchen Sie das Verhalten von f(x) an der Definitionslücke.
b) Untersuchen Sie das Verhalten von f(x) für x
= IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten und die Nullstellen von f und
untersuchen Sie das Verhalten von f(x) an der Definitionslücke.
b) Untersuchen Sie das Verhalten von f(x) für x  ±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G
±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G .
Zeigen Sie, dass G
.
Zeigen Sie, dass G keine Wendepunkte besitzt.
d) Zeichnen Sie G
keine Wendepunkte besitzt.
d) Zeichnen Sie G im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Berechnen Sie
im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Berechnen Sie 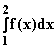 .
. 4. Gegeben ist die Funktion f : x
4. Gegeben ist die Funktion f : x 
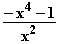 mit ID
mit ID = IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten von G
= IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten von G und das Verhalten von f(x)
an der Definitionslücke. Zeigen Sie, dass f keine Nullstelle besitzt und sein
Graf nur im 3. und 4. Quadranten verläuft.
b) Untersuchen Sie das Verhalten von f(x) für x
und das Verhalten von f(x)
an der Definitionslücke. Zeigen Sie, dass f keine Nullstelle besitzt und sein
Graf nur im 3. und 4. Quadranten verläuft.
b) Untersuchen Sie das Verhalten von f(x) für x  ±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G
±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G .
Zeigen Sie, dass G
.
Zeigen Sie, dass G keine Wendepunkte besitzt.
d) Zeichnen Sie G
keine Wendepunkte besitzt.
d) Zeichnen Sie G im Intervall –2 ≤ x ≤ 2. (1 LE = 2 cm)
e) Geben Sie die Menge aller Stammfunktionen von f an.
Bestimmen Sie diejenige Stammfunktion F von f, für die gilt: F(1) = 2.
f) Berechnen Sie den Inhalt der Fläche, die von G
im Intervall –2 ≤ x ≤ 2. (1 LE = 2 cm)
e) Geben Sie die Menge aller Stammfunktionen von f an.
Bestimmen Sie diejenige Stammfunktion F von f, für die gilt: F(1) = 2.
f) Berechnen Sie den Inhalt der Fläche, die von G und der Geraden mit der
Gleichung y = –2,5 im 4. Quadranten eingeschlossen wird.
g) Der Graf von f schließt für x ≥ 1 mit der Parabel y = –x
und der Geraden mit der
Gleichung y = –2,5 im 4. Quadranten eingeschlossen wird.
g) Der Graf von f schließt für x ≥ 1 mit der Parabel y = –x und der Geraden
x = 1 eine Fläche ein, die sich ins Unendliche erstreckt. Bestimmen Sie
deren Inhalt.
und der Geraden
x = 1 eine Fläche ein, die sich ins Unendliche erstreckt. Bestimmen Sie
deren Inhalt.  5. Gegeben ist die Funktion f : x
5. Gegeben ist die Funktion f : x 
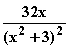 mit ID
mit ID = IR .
a) Bestimmen Sie das Symmetrieverhalten von G
= IR .
a) Bestimmen Sie das Symmetrieverhalten von G und das Verhalten von f(x)
für x
und das Verhalten von f(x)
für x  ±∞. Zeigen Sie, dass G
±∞. Zeigen Sie, dass G nur im 1. und 3. Quadranten verläuft.
Fertigen Sie aufgrund dieser Erkenntnisse eine Grobskizze von G
nur im 1. und 3. Quadranten verläuft.
Fertigen Sie aufgrund dieser Erkenntnisse eine Grobskizze von G .
Wieviele Wendepunkte wird G
.
Wieviele Wendepunkte wird G besitzen?
b) Bestimmen Sie nun Art und Lage der Extrem- und Wendepunkte von G
besitzen?
b) Bestimmen Sie nun Art und Lage der Extrem- und Wendepunkte von G .
c) Stellen Sie die Gleichungen der drei Wendetangenten auf.
d) Zeichnen Sie G
.
c) Stellen Sie die Gleichungen der drei Wendetangenten auf.
d) Zeichnen Sie G im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Zeigen Sie, dass die Funktion F : x
im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Zeigen Sie, dass die Funktion F : x 
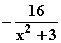 mit ID
mit ID = IR eine Stamm-
funktion von f ist.
f) Berechnen Sie den Inhalt der Gesamtfläche, die von G
= IR eine Stamm-
funktion von f ist.
f) Berechnen Sie den Inhalt der Gesamtfläche, die von G und seiner
Asymptoten eingeschlossen wird.
und seiner
Asymptoten eingeschlossen wird. 6. Gegeben ist die Funktion f : x
6. Gegeben ist die Funktion f : x 
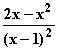 mit ID
mit ID = IR \ {1}.
a) Bestimmen Sie die Nullstellen der Funktion f und die Asymptoten ihres
Grafen.
b) Geben Sie die Bereiche an, in denen G
= IR \ {1}.
a) Bestimmen Sie die Nullstellen der Funktion f und die Asymptoten ihres
Grafen.
b) Geben Sie die Bereiche an, in denen G steigt bzw. fällt.
c) Zeichnen Sie G
steigt bzw. fällt.
c) Zeichnen Sie G im Intervall –2 ≤ x ≤ 4.
d) Zeigen Sie, dass die Funktion F : x
im Intervall –2 ≤ x ≤ 4.
d) Zeigen Sie, dass die Funktion F : x 
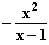 mit ID
mit ID = ID
= ID eine Stamm-
funktion von f ist.
e) Ermitteln Sie die Extrempunkte und Asymptoten von GF.
f) Von G
eine Stamm-
funktion von f ist.
e) Ermitteln Sie die Extrempunkte und Asymptoten von GF.
f) Von G und den drei Geraden x = 2, x = 4 und y = –1 wird eine Fläche
eingeschlossen. Berechnen Sie deren Inhalt.
und den drei Geraden x = 2, x = 4 und y = –1 wird eine Fläche
eingeschlossen. Berechnen Sie deren Inhalt. 7. Gegeben sind die Funktionen
f : x
7. Gegeben sind die Funktionen
f : x  x
x – 3x – 2 , g : x
– 3x – 2 , g : x 
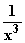 (x
(x – 3x – 2) und
h : x
– 3x – 2) und
h : x 
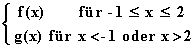 .
a) Diskutieren Sie die Funktionen f und g und fertigen Sie eine Skizze an.
b) Zeigen Sie, dass die Funktion h an der Stelle x = –1 stetig und sogar
differenzierbar ist.
c) Kennzeichnen Sie in der Skizze den Grafen von h mit anderer Farbe.
d) Die Geraden y = 1, x = 0 und x = k mit k > 2 begrenzen mit dem
Grafen von h ein Flächenstück A(k). Berechnen Sie dessen Inhalt.
Bestimmen Sie den Grenzwert von A(k) für k
.
a) Diskutieren Sie die Funktionen f und g und fertigen Sie eine Skizze an.
b) Zeigen Sie, dass die Funktion h an der Stelle x = –1 stetig und sogar
differenzierbar ist.
c) Kennzeichnen Sie in der Skizze den Grafen von h mit anderer Farbe.
d) Die Geraden y = 1, x = 0 und x = k mit k > 2 begrenzen mit dem
Grafen von h ein Flächenstück A(k). Berechnen Sie dessen Inhalt.
Bestimmen Sie den Grenzwert von A(k) für k  ∞.
∞. 8. Gesucht ist eine rationale Funktion f mit möglichst niedrigem Zähler- und
Nennergrad (Nennergrad > 0), die folgende Eigenschaften besitzt:
a) Ihr Graf ist punktsymmetrisch zum Ursprung und besitzt die Winkel-
halbierende des 1. und 3. Quadranten als Asymptote.
b) Ihr Graf ist achsensymmetrisch zur y-Achse, besitzt die Gerade y = 1
als Asymptote und hat den Hochpunkt (0|–1).
c) Ihr Graf hat keine senkrechte Asymptote und berührt die Parabel y = 4 – x
8. Gesucht ist eine rationale Funktion f mit möglichst niedrigem Zähler- und
Nennergrad (Nennergrad > 0), die folgende Eigenschaften besitzt:
a) Ihr Graf ist punktsymmetrisch zum Ursprung und besitzt die Winkel-
halbierende des 1. und 3. Quadranten als Asymptote.
b) Ihr Graf ist achsensymmetrisch zur y-Achse, besitzt die Gerade y = 1
als Asymptote und hat den Hochpunkt (0|–1).
c) Ihr Graf hat keine senkrechte Asymptote und berührt die Parabel y = 4 – x bei x = 2.
d) Ihr Graf besitzt die Asymptoten x = 0 und y = x + 1 und schneidet seine
schiefe Asymptote bei x = 1.
e) Ihr Graf ist im Punkt (2|0) unterbrochen, und bei x = –1 streben
ihre Funktionswerte beidseitig nach +∞.
f) Ihr Graf besitzt die asymptotische Kurve y = x
bei x = 2.
d) Ihr Graf besitzt die Asymptoten x = 0 und y = x + 1 und schneidet seine
schiefe Asymptote bei x = 1.
e) Ihr Graf ist im Punkt (2|0) unterbrochen, und bei x = –1 streben
ihre Funktionswerte beidseitig nach +∞.
f) Ihr Graf besitzt die asymptotische Kurve y = x – 1 und den Tiefpunkt
TIP(1|2).
– 1 und den Tiefpunkt
TIP(1|2). 9. Abschlussprüfung an Berufsoberschulen 2001
Auszug aus der Aufgabengruppe A I mit leichten formalen Änderungen:
Gegeben sind die Funktion
f : x
9. Abschlussprüfung an Berufsoberschulen 2001
Auszug aus der Aufgabengruppe A I mit leichten formalen Änderungen:
Gegeben sind die Funktion
f : x  f(x) =
f(x) = 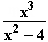 sowie die Funktionenschar f
sowie die Funktionenschar f : x
: x  f
f (x) =
(x) = 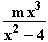 mit m
mit m 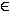 IR \ {0}
und jeweils maximaler reeller Definitionsmenge.
a) Untersuchen Sie den Grafen der Funktion f auf Symmetrie bzgl.
des Koordinatensystems.
b) Untersuchen Sie das Verhalten der Funktion f an ihren Definitionslücken.
c) Geben Sie die Gleichungen aller Asymptoten des Grafen von f an.
d) Bestimmen Sie ohne Verwendung der zweiten Ableitung die exakten
Koordinaten und die Art der Extrempunkte des Grafen von f.
e) In der folgenden Grafik sind die Winkelhalbierende des I. Quadranten
sowie der Graf von f für 0 ≤ x ≤ 10 eingetragen.
IR \ {0}
und jeweils maximaler reeller Definitionsmenge.
a) Untersuchen Sie den Grafen der Funktion f auf Symmetrie bzgl.
des Koordinatensystems.
b) Untersuchen Sie das Verhalten der Funktion f an ihren Definitionslücken.
c) Geben Sie die Gleichungen aller Asymptoten des Grafen von f an.
d) Bestimmen Sie ohne Verwendung der zweiten Ableitung die exakten
Koordinaten und die Art der Extrempunkte des Grafen von f.
e) In der folgenden Grafik sind die Winkelhalbierende des I. Quadranten
sowie der Graf von f für 0 ≤ x ≤ 10 eingetragen.
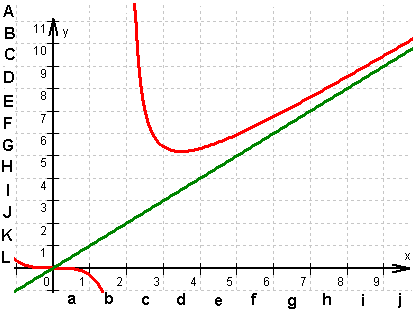 Ermitteln Sie aus der Grafik einen ganzzahligen Näherungswert für
das Integral
Ermitteln Sie aus der Grafik einen ganzzahligen Näherungswert für
das Integral 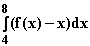 .
Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate,
die mit Buchstabenkombinationen bezeichnet werden.
f) Untersuchen Sie, welchen Einfluss der Parameter m auf den Verlauf des
Grafen von f
.
Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate,
die mit Buchstabenkombinationen bezeichnet werden.
f) Untersuchen Sie, welchen Einfluss der Parameter m auf den Verlauf des
Grafen von f im Vergleich zum Grafen von f hat.
Gehen Sie dabei auf die Fälle m > 0, m < 0, |m| < 1 und |m| > 1 ein.
Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und Art
der Extrempunkte des Grafen von f
im Vergleich zum Grafen von f hat.
Gehen Sie dabei auf die Fälle m > 0, m < 0, |m| < 1 und |m| > 1 ein.
Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und Art
der Extrempunkte des Grafen von f an.
an. 10. Gegeben ist die rationale Funktionenschar h
10. Gegeben ist die rationale Funktionenschar h : x
: x 
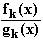 , k
, k 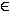 IR\{0},
mit folgenden Bedingungen:
1) Der Graf von h
IR\{0},
mit folgenden Bedingungen:
1) Der Graf von h besitzt eine waagrechte Asymptote.
2) f
besitzt eine waagrechte Asymptote.
2) f ist eine ganz-rationale Funktion 3. Grades, deren Graf bei x = 0
die Wendetangente y = –3k²x + 2k³ besitzt.
3) g
ist eine ganz-rationale Funktion 3. Grades, deren Graf bei x = 0
die Wendetangente y = –3k²x + 2k³ besitzt.
3) g ist eine ganz-rationale Funktion, deren Graf punktsymmetrisch bzgl. des
Koordinatenursprungs ist und bei x = k die Steigung –k³ besitzt.
4) h
ist eine ganz-rationale Funktion, deren Graf punktsymmetrisch bzgl. des
Koordinatenursprungs ist und bei x = k die Steigung –k³ besitzt.
4) h besitzt die hebbare Definitionslücke x = –2k.
a) Bestimmen Sie die Gleichung der Funktion h
besitzt die hebbare Definitionslücke x = –2k.
a) Bestimmen Sie die Gleichung der Funktion h .
(Zur Orientierung: f
.
(Zur Orientierung: f (x) = x³ – 3k²x + 2k³; g
(x) = x³ – 3k²x + 2k³; g (x) = kx³ – 4k³x)
b) Geben Sie den maximalen Definitionsbereich der Funktion h
(x) = kx³ – 4k³x)
b) Geben Sie den maximalen Definitionsbereich der Funktion h an und
untersuchen Sie ihr Verhalten in der Umgebung ihrer Definitionslücken.
c) Bestimmen Sie die Nullstellen sowie die Gleichungen aller Asymptoten
des Grafen von h
an und
untersuchen Sie ihr Verhalten in der Umgebung ihrer Definitionslücken.
c) Bestimmen Sie die Nullstellen sowie die Gleichungen aller Asymptoten
des Grafen von h .
d) Ermitteln Sie ohne Verwendung der zweiten Ableitung die Art und die
Koordinaten eventueller Extrempunkte des Grafen von h
.
d) Ermitteln Sie ohne Verwendung der zweiten Ableitung die Art und die
Koordinaten eventueller Extrempunkte des Grafen von h .
e) Skizzieren Sie den Grafen von h
.
e) Skizzieren Sie den Grafen von h im Bereich –3 ≤ x ≤ 5. (1 LE = 2 cm)
f) Schließen Sie ohne weitere Rechnung aus den bisherigen Ergebnissen auf die
Anzahl der Wendepunkte des Grafen von h
im Bereich –3 ≤ x ≤ 5. (1 LE = 2 cm)
f) Schließen Sie ohne weitere Rechnung aus den bisherigen Ergebnissen auf die
Anzahl der Wendepunkte des Grafen von h sowie auf sein Krümmungs-
verhalten in Abhängigkeit von k.
sowie auf sein Krümmungs-
verhalten in Abhängigkeit von k. 11. Eine leere zylindrische Getränkedose hat die Höhe H, die
11. Eine leere zylindrische Getränkedose hat die Höhe H, die 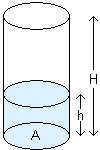 Grundfläche A und die Masse M. Ihre Wandstärke soll ver–
nachlässigt werden. Diese Dose soll bis zur Höhe h mit
Wasser gefüllt werden und besitzt dann einen Schwerpunkt
s(h), der auf der Strecke zwischen den Schwerpunkten sD
der leeren Dose und sW der Wassersäule liegt.
a) Drücken Sie die Schwerpunkte sD und sW durch
die gegebenen Höhen aus.
b) Der Gesamtschwerpunkt s(h) lässt sich analog zum Erwartungswert einer
Zufallsgröße aus den Schwerpunkten sD und sW bestimmen, indem diese
mit den Verhältnissen der Masse der leeren Dose bzw der Masse der Wasser-
säule zur Gesamtmasse der teilweise gefüllten Dose multipliziert und dann
die derart „gewichteten“ Schwerpunkte addiert werden.
Drücken Sie nach diesen Hinweisen s(h) durch die Variable h sowie durch
die Konstanten H, A und M aus. Beachten Sie dabei, dass die Dichte des
Wassers 1
Grundfläche A und die Masse M. Ihre Wandstärke soll ver–
nachlässigt werden. Diese Dose soll bis zur Höhe h mit
Wasser gefüllt werden und besitzt dann einen Schwerpunkt
s(h), der auf der Strecke zwischen den Schwerpunkten sD
der leeren Dose und sW der Wassersäule liegt.
a) Drücken Sie die Schwerpunkte sD und sW durch
die gegebenen Höhen aus.
b) Der Gesamtschwerpunkt s(h) lässt sich analog zum Erwartungswert einer
Zufallsgröße aus den Schwerpunkten sD und sW bestimmen, indem diese
mit den Verhältnissen der Masse der leeren Dose bzw der Masse der Wasser-
säule zur Gesamtmasse der teilweise gefüllten Dose multipliziert und dann
die derart „gewichteten“ Schwerpunkte addiert werden.
Drücken Sie nach diesen Hinweisen s(h) durch die Variable h sowie durch
die Konstanten H, A und M aus. Beachten Sie dabei, dass die Dichte des
Wassers 1 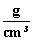 beträgt.
c) Die teilweise gefüllte Dose steht am stabilsten, wenn ihr Gesamtschwerpunkt
s(h) möglichst niedrig ist.
Wie hoch muss der Wasserspiegel stehen, damit die Dose am stabilsten steht?
d) Messen Sie alle erforderlichen Größen an einer von Ihnen gewählten leeren
Getränkedose, und berechnen Sie dann den für den stabilsten Stand dieser
Dose nötigen Wasserspiegel.
beträgt.
c) Die teilweise gefüllte Dose steht am stabilsten, wenn ihr Gesamtschwerpunkt
s(h) möglichst niedrig ist.
Wie hoch muss der Wasserspiegel stehen, damit die Dose am stabilsten steht?
d) Messen Sie alle erforderlichen Größen an einer von Ihnen gewählten leeren
Getränkedose, und berechnen Sie dann den für den stabilsten Stand dieser
Dose nötigen Wasserspiegel.
 : x
: x 
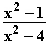 , f
, f : x
: x 
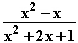 ,
f
,
f : x
: x 
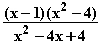 , f
, f : x
: x 
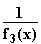 mit jeweils maximaler reeller Definitionsmenge.
a) Bestimmen Sie jeweils die Definitionslücken und die Nullstellen.
b) Welches Verhalten zeigt die jeweilige Funktion in der Umgebung ihrer
Definitionslücken?
mit jeweils maximaler reeller Definitionsmenge.
a) Bestimmen Sie jeweils die Definitionslücken und die Nullstellen.
b) Welches Verhalten zeigt die jeweilige Funktion in der Umgebung ihrer
Definitionslücken?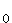 : x
: x 
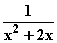 und f
und f : x
: x 
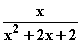 mit jeweils max. Definitionsmenge
sowie f
mit jeweils max. Definitionsmenge
sowie f , f
, f und f
und f aus Aufgabe 1.
a) Bestimmen Sie jeweils die Gleichungen der Asymptoten.
b) Wo verläuft der Graf der jeweiligen Funktion oberhalb, wo unterhalb
seiner nichtsenkrechten Asymptote?
c) Untersuchen Sie das Monotonieverhalten der jeweiligen Funktionen, und
geben Sie ggf. die Art und die Koordinaten der Extrempunkte an.
d) Fertigen Sie Skizzen der jeweiligen Grafen.
aus Aufgabe 1.
a) Bestimmen Sie jeweils die Gleichungen der Asymptoten.
b) Wo verläuft der Graf der jeweiligen Funktion oberhalb, wo unterhalb
seiner nichtsenkrechten Asymptote?
c) Untersuchen Sie das Monotonieverhalten der jeweiligen Funktionen, und
geben Sie ggf. die Art und die Koordinaten der Extrempunkte an.
d) Fertigen Sie Skizzen der jeweiligen Grafen.
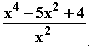 mit ID
mit ID = IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten und die Nullstellen von f und
untersuchen Sie das Verhalten von f(x) an der Definitionslücke.
b) Untersuchen Sie das Verhalten von f(x) für x
= IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten und die Nullstellen von f und
untersuchen Sie das Verhalten von f(x) an der Definitionslücke.
b) Untersuchen Sie das Verhalten von f(x) für x  ±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G
±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G .
Zeigen Sie, dass G
.
Zeigen Sie, dass G keine Wendepunkte besitzt.
d) Zeichnen Sie G
keine Wendepunkte besitzt.
d) Zeichnen Sie G im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Berechnen Sie
im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Berechnen Sie 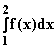 .
.
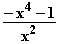 mit ID
mit ID = IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten von G
= IR \ {0}.
a) Bestimmen Sie das Symmetrieverhalten von G und das Verhalten von f(x)
an der Definitionslücke. Zeigen Sie, dass f keine Nullstelle besitzt und sein
Graf nur im 3. und 4. Quadranten verläuft.
b) Untersuchen Sie das Verhalten von f(x) für x
und das Verhalten von f(x)
an der Definitionslücke. Zeigen Sie, dass f keine Nullstelle besitzt und sein
Graf nur im 3. und 4. Quadranten verläuft.
b) Untersuchen Sie das Verhalten von f(x) für x  ±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G
±∞ und geben Sie die
Gleichung der asymptotischen Kurve an.
c) Bestimmen Sie Art und Lage der Extrempunkte von G .
Zeigen Sie, dass G
.
Zeigen Sie, dass G keine Wendepunkte besitzt.
d) Zeichnen Sie G
keine Wendepunkte besitzt.
d) Zeichnen Sie G im Intervall –2 ≤ x ≤ 2. (1 LE = 2 cm)
e) Geben Sie die Menge aller Stammfunktionen von f an.
Bestimmen Sie diejenige Stammfunktion F von f, für die gilt: F(1) = 2.
f) Berechnen Sie den Inhalt der Fläche, die von G
im Intervall –2 ≤ x ≤ 2. (1 LE = 2 cm)
e) Geben Sie die Menge aller Stammfunktionen von f an.
Bestimmen Sie diejenige Stammfunktion F von f, für die gilt: F(1) = 2.
f) Berechnen Sie den Inhalt der Fläche, die von G und der Geraden mit der
Gleichung y = –2,5 im 4. Quadranten eingeschlossen wird.
g) Der Graf von f schließt für x ≥ 1 mit der Parabel y = –x
und der Geraden mit der
Gleichung y = –2,5 im 4. Quadranten eingeschlossen wird.
g) Der Graf von f schließt für x ≥ 1 mit der Parabel y = –x und der Geraden
x = 1 eine Fläche ein, die sich ins Unendliche erstreckt. Bestimmen Sie
deren Inhalt.
und der Geraden
x = 1 eine Fläche ein, die sich ins Unendliche erstreckt. Bestimmen Sie
deren Inhalt. 
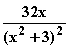 mit ID
mit ID = IR .
a) Bestimmen Sie das Symmetrieverhalten von G
= IR .
a) Bestimmen Sie das Symmetrieverhalten von G und das Verhalten von f(x)
für x
und das Verhalten von f(x)
für x  ±∞. Zeigen Sie, dass G
±∞. Zeigen Sie, dass G nur im 1. und 3. Quadranten verläuft.
Fertigen Sie aufgrund dieser Erkenntnisse eine Grobskizze von G
nur im 1. und 3. Quadranten verläuft.
Fertigen Sie aufgrund dieser Erkenntnisse eine Grobskizze von G .
Wieviele Wendepunkte wird G
.
Wieviele Wendepunkte wird G besitzen?
b) Bestimmen Sie nun Art und Lage der Extrem- und Wendepunkte von G
besitzen?
b) Bestimmen Sie nun Art und Lage der Extrem- und Wendepunkte von G .
c) Stellen Sie die Gleichungen der drei Wendetangenten auf.
d) Zeichnen Sie G
.
c) Stellen Sie die Gleichungen der drei Wendetangenten auf.
d) Zeichnen Sie G im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Zeigen Sie, dass die Funktion F : x
im Intervall –3 ≤ x ≤ 3. (1 LE = 2 cm)
e) Zeigen Sie, dass die Funktion F : x 
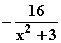 mit ID
mit ID = IR eine Stamm-
funktion von f ist.
f) Berechnen Sie den Inhalt der Gesamtfläche, die von G
= IR eine Stamm-
funktion von f ist.
f) Berechnen Sie den Inhalt der Gesamtfläche, die von G und seiner
Asymptoten eingeschlossen wird.
und seiner
Asymptoten eingeschlossen wird.
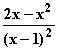 mit ID
mit ID = IR \ {1}.
a) Bestimmen Sie die Nullstellen der Funktion f und die Asymptoten ihres
Grafen.
b) Geben Sie die Bereiche an, in denen G
= IR \ {1}.
a) Bestimmen Sie die Nullstellen der Funktion f und die Asymptoten ihres
Grafen.
b) Geben Sie die Bereiche an, in denen G steigt bzw. fällt.
c) Zeichnen Sie G
steigt bzw. fällt.
c) Zeichnen Sie G im Intervall –2 ≤ x ≤ 4.
d) Zeigen Sie, dass die Funktion F : x
im Intervall –2 ≤ x ≤ 4.
d) Zeigen Sie, dass die Funktion F : x 
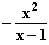 mit ID
mit ID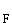 = ID
= ID eine Stamm-
funktion von f ist.
e) Ermitteln Sie die Extrempunkte und Asymptoten von GF.
f) Von G
eine Stamm-
funktion von f ist.
e) Ermitteln Sie die Extrempunkte und Asymptoten von GF.
f) Von G und den drei Geraden x = 2, x = 4 und y = –1 wird eine Fläche
eingeschlossen. Berechnen Sie deren Inhalt.
und den drei Geraden x = 2, x = 4 und y = –1 wird eine Fläche
eingeschlossen. Berechnen Sie deren Inhalt. x
x – 3x – 2 , g : x
– 3x – 2 , g : x 
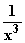 (x
(x – 3x – 2) und
h : x
– 3x – 2) und
h : x 
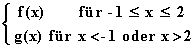 .
a) Diskutieren Sie die Funktionen f und g und fertigen Sie eine Skizze an.
b) Zeigen Sie, dass die Funktion h an der Stelle x = –1 stetig und sogar
differenzierbar ist.
c) Kennzeichnen Sie in der Skizze den Grafen von h mit anderer Farbe.
d) Die Geraden y = 1, x = 0 und x = k mit k > 2 begrenzen mit dem
Grafen von h ein Flächenstück A(k). Berechnen Sie dessen Inhalt.
Bestimmen Sie den Grenzwert von A(k) für k
.
a) Diskutieren Sie die Funktionen f und g und fertigen Sie eine Skizze an.
b) Zeigen Sie, dass die Funktion h an der Stelle x = –1 stetig und sogar
differenzierbar ist.
c) Kennzeichnen Sie in der Skizze den Grafen von h mit anderer Farbe.
d) Die Geraden y = 1, x = 0 und x = k mit k > 2 begrenzen mit dem
Grafen von h ein Flächenstück A(k). Berechnen Sie dessen Inhalt.
Bestimmen Sie den Grenzwert von A(k) für k  ∞.
∞. bei x = 2.
d) Ihr Graf besitzt die Asymptoten x = 0 und y = x + 1 und schneidet seine
schiefe Asymptote bei x = 1.
e) Ihr Graf ist im Punkt (2|0) unterbrochen, und bei x = –1 streben
ihre Funktionswerte beidseitig nach +∞.
f) Ihr Graf besitzt die asymptotische Kurve y = x
bei x = 2.
d) Ihr Graf besitzt die Asymptoten x = 0 und y = x + 1 und schneidet seine
schiefe Asymptote bei x = 1.
e) Ihr Graf ist im Punkt (2|0) unterbrochen, und bei x = –1 streben
ihre Funktionswerte beidseitig nach +∞.
f) Ihr Graf besitzt die asymptotische Kurve y = x – 1 und den Tiefpunkt
TIP(1|2).
– 1 und den Tiefpunkt
TIP(1|2). f(x) =
f(x) = 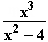 sowie die Funktionenschar f
sowie die Funktionenschar f : x
: x  f
f (x) =
(x) = 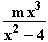 mit m
mit m 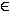 IR \ {0}
und jeweils maximaler reeller Definitionsmenge.
a) Untersuchen Sie den Grafen der Funktion f auf Symmetrie bzgl.
des Koordinatensystems.
b) Untersuchen Sie das Verhalten der Funktion f an ihren Definitionslücken.
c) Geben Sie die Gleichungen aller Asymptoten des Grafen von f an.
d) Bestimmen Sie ohne Verwendung der zweiten Ableitung die exakten
Koordinaten und die Art der Extrempunkte des Grafen von f.
e) In der folgenden Grafik sind die Winkelhalbierende des I. Quadranten
sowie der Graf von f für 0 ≤ x ≤ 10 eingetragen.
IR \ {0}
und jeweils maximaler reeller Definitionsmenge.
a) Untersuchen Sie den Grafen der Funktion f auf Symmetrie bzgl.
des Koordinatensystems.
b) Untersuchen Sie das Verhalten der Funktion f an ihren Definitionslücken.
c) Geben Sie die Gleichungen aller Asymptoten des Grafen von f an.
d) Bestimmen Sie ohne Verwendung der zweiten Ableitung die exakten
Koordinaten und die Art der Extrempunkte des Grafen von f.
e) In der folgenden Grafik sind die Winkelhalbierende des I. Quadranten
sowie der Graf von f für 0 ≤ x ≤ 10 eingetragen.

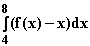 .
Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate,
die mit Buchstabenkombinationen bezeichnet werden.
f) Untersuchen Sie, welchen Einfluss der Parameter m auf den Verlauf des
Grafen von f
.
Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate,
die mit Buchstabenkombinationen bezeichnet werden.
f) Untersuchen Sie, welchen Einfluss der Parameter m auf den Verlauf des
Grafen von f im Vergleich zum Grafen von f hat.
Gehen Sie dabei auf die Fälle m > 0, m < 0, |m| < 1 und |m| > 1 ein.
Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und Art
der Extrempunkte des Grafen von f
im Vergleich zum Grafen von f hat.
Gehen Sie dabei auf die Fälle m > 0, m < 0, |m| < 1 und |m| > 1 ein.
Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und Art
der Extrempunkte des Grafen von f an.
an. : x
: x 
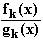 , k
, k 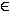 IR\{0},
mit folgenden Bedingungen:
1) Der Graf von h
IR\{0},
mit folgenden Bedingungen:
1) Der Graf von h besitzt eine waagrechte Asymptote.
2) f
besitzt eine waagrechte Asymptote.
2) f ist eine ganz-rationale Funktion 3. Grades, deren Graf bei x = 0
die Wendetangente y = –3k²x + 2k³ besitzt.
3) g
ist eine ganz-rationale Funktion 3. Grades, deren Graf bei x = 0
die Wendetangente y = –3k²x + 2k³ besitzt.
3) g ist eine ganz-rationale Funktion, deren Graf punktsymmetrisch bzgl. des
Koordinatenursprungs ist und bei x = k die Steigung –k³ besitzt.
4) h
ist eine ganz-rationale Funktion, deren Graf punktsymmetrisch bzgl. des
Koordinatenursprungs ist und bei x = k die Steigung –k³ besitzt.
4) h besitzt die hebbare Definitionslücke x = –2k.
a) Bestimmen Sie die Gleichung der Funktion h
besitzt die hebbare Definitionslücke x = –2k.
a) Bestimmen Sie die Gleichung der Funktion h .
(Zur Orientierung: f
.
(Zur Orientierung: f (x) = x³ – 3k²x + 2k³; g
(x) = x³ – 3k²x + 2k³; g (x) = kx³ – 4k³x)
b) Geben Sie den maximalen Definitionsbereich der Funktion h
(x) = kx³ – 4k³x)
b) Geben Sie den maximalen Definitionsbereich der Funktion h an und
untersuchen Sie ihr Verhalten in der Umgebung ihrer Definitionslücken.
c) Bestimmen Sie die Nullstellen sowie die Gleichungen aller Asymptoten
des Grafen von h
an und
untersuchen Sie ihr Verhalten in der Umgebung ihrer Definitionslücken.
c) Bestimmen Sie die Nullstellen sowie die Gleichungen aller Asymptoten
des Grafen von h .
d) Ermitteln Sie ohne Verwendung der zweiten Ableitung die Art und die
Koordinaten eventueller Extrempunkte des Grafen von h
.
d) Ermitteln Sie ohne Verwendung der zweiten Ableitung die Art und die
Koordinaten eventueller Extrempunkte des Grafen von h .
e) Skizzieren Sie den Grafen von h
.
e) Skizzieren Sie den Grafen von h im Bereich –3 ≤ x ≤ 5. (1 LE = 2 cm)
f) Schließen Sie ohne weitere Rechnung aus den bisherigen Ergebnissen auf die
Anzahl der Wendepunkte des Grafen von h
im Bereich –3 ≤ x ≤ 5. (1 LE = 2 cm)
f) Schließen Sie ohne weitere Rechnung aus den bisherigen Ergebnissen auf die
Anzahl der Wendepunkte des Grafen von h sowie auf sein Krümmungs-
verhalten in Abhängigkeit von k.
sowie auf sein Krümmungs-
verhalten in Abhängigkeit von k. Grundfläche A und die Masse M. Ihre Wandstärke soll ver–
nachlässigt werden. Diese Dose soll bis zur Höhe h mit
Wasser gefüllt werden und besitzt dann einen Schwerpunkt
s(h), der auf der Strecke zwischen den Schwerpunkten sD
der leeren Dose und sW der Wassersäule liegt.
a) Drücken Sie die Schwerpunkte sD und sW durch
die gegebenen Höhen aus.
b) Der Gesamtschwerpunkt s(h) lässt sich analog zum Erwartungswert einer
Zufallsgröße aus den Schwerpunkten sD und sW bestimmen, indem diese
mit den Verhältnissen der Masse der leeren Dose bzw der Masse der Wasser-
säule zur Gesamtmasse der teilweise gefüllten Dose multipliziert und dann
die derart „gewichteten“ Schwerpunkte addiert werden.
Drücken Sie nach diesen Hinweisen s(h) durch die Variable h sowie durch
die Konstanten H, A und M aus. Beachten Sie dabei, dass die Dichte des
Wassers 1
Grundfläche A und die Masse M. Ihre Wandstärke soll ver–
nachlässigt werden. Diese Dose soll bis zur Höhe h mit
Wasser gefüllt werden und besitzt dann einen Schwerpunkt
s(h), der auf der Strecke zwischen den Schwerpunkten sD
der leeren Dose und sW der Wassersäule liegt.
a) Drücken Sie die Schwerpunkte sD und sW durch
die gegebenen Höhen aus.
b) Der Gesamtschwerpunkt s(h) lässt sich analog zum Erwartungswert einer
Zufallsgröße aus den Schwerpunkten sD und sW bestimmen, indem diese
mit den Verhältnissen der Masse der leeren Dose bzw der Masse der Wasser-
säule zur Gesamtmasse der teilweise gefüllten Dose multipliziert und dann
die derart „gewichteten“ Schwerpunkte addiert werden.
Drücken Sie nach diesen Hinweisen s(h) durch die Variable h sowie durch
die Konstanten H, A und M aus. Beachten Sie dabei, dass die Dichte des
Wassers 1 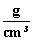 beträgt.
c) Die teilweise gefüllte Dose steht am stabilsten, wenn ihr Gesamtschwerpunkt
s(h) möglichst niedrig ist.
Wie hoch muss der Wasserspiegel stehen, damit die Dose am stabilsten steht?
d) Messen Sie alle erforderlichen Größen an einer von Ihnen gewählten leeren
Getränkedose, und berechnen Sie dann den für den stabilsten Stand dieser
Dose nötigen Wasserspiegel.
beträgt.
c) Die teilweise gefüllte Dose steht am stabilsten, wenn ihr Gesamtschwerpunkt
s(h) möglichst niedrig ist.
Wie hoch muss der Wasserspiegel stehen, damit die Dose am stabilsten steht?
d) Messen Sie alle erforderlichen Größen an einer von Ihnen gewählten leeren
Getränkedose, und berechnen Sie dann den für den stabilsten Stand dieser
Dose nötigen Wasserspiegel.