1.

Gegeben ist die Funktion f mit der Gleichung .

1.1

Bestimmen Sie den maximalen Definitionsbereich von f sowie die Schnittpunkte des Graphen von f mit den Koordinatenachsen.

4

1.2

Untersuchen Sie das Verhalten an den Rändern des Definitionsbereichs. Wenden Sie dabei gegebenenfalls die Regel von de L'Hospital an.
Geben Sie auch alle Asymptoten des Graphen von f an.

7

1.3

Berechnen Sie die Koordinaten des Extrempunkts des Graphen von f und bestimmen Sie seine Art mit einer Monotonietabelle.
[ Zwischenergebnis: ]

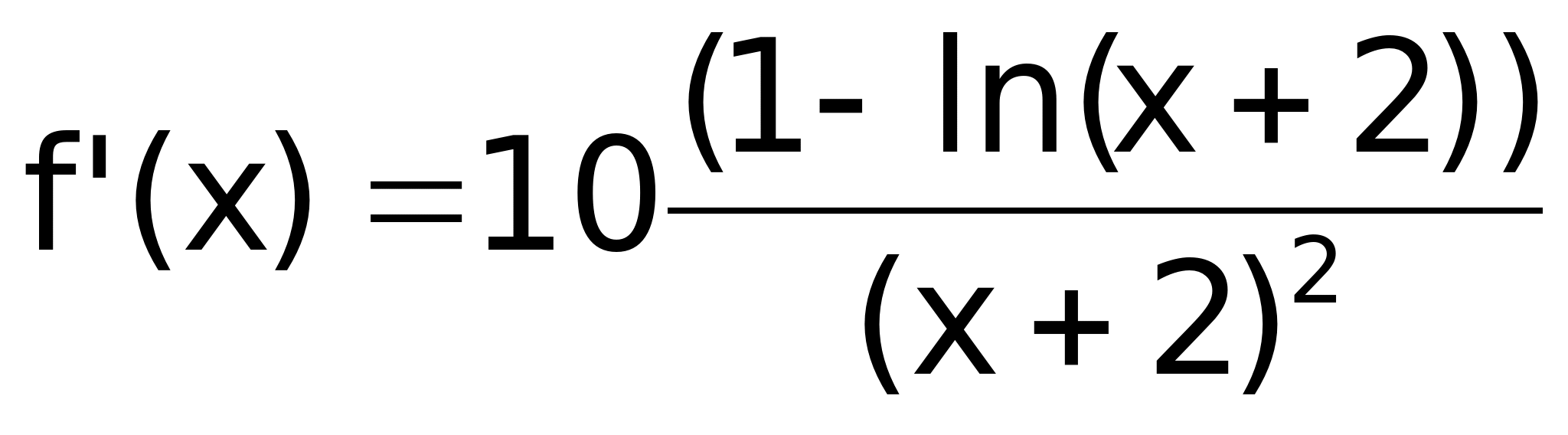8

1.4

Skizzieren Sie den Graphen und seine Asymptoten unter Verwendung bisheriger Ergebnisse in ein Koordinatensystem. Schließen Sie aus dem Verlauf des Graphen auf die Anzahl der Wendepunkte.

5

2.

Gegeben ist folgender Ausschnitt des Graphen einer Funktion g und seiner waagrechten Asymptote mit D = [–1 ; ∞[.

Betrachten Sie dazu die Funktion h mit h(x)=ln(g(x)).

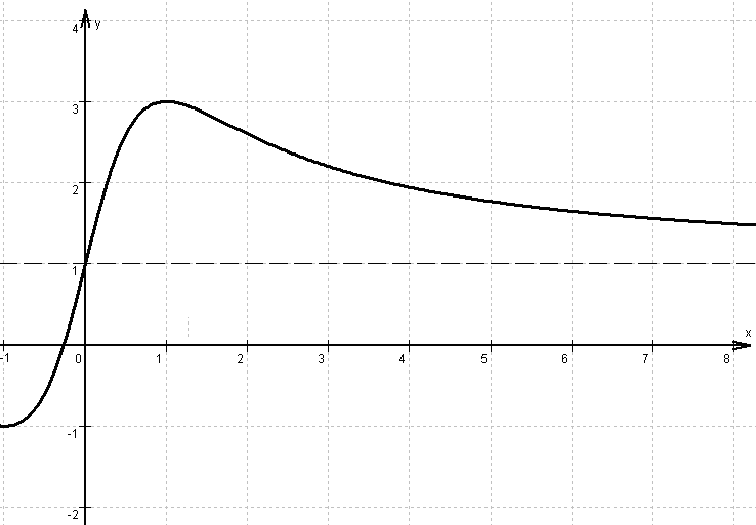
2.1

Geben Sie den Definitionsbereich von h(x) sowie eventuell vorhandene Nullstellen und Koordinaten von Extrempunkten des Graphen von h an.

4

2.2

Besitzt der Graph von h Asymptoten? Geben Sie deren Gleichung an, falls möglich.

2

2.3

Skizzieren Sie den Graph von h so genau wie möglich in das beiliegende Koordinatensystem.

3