1.0
Gegeben ist die Funktion 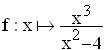 mit der Definitionsmenge
mit der Definitionsmenge 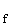 = IR \{–2; 2}.
= IR \{–2; 2}.
Zeigen Sie, dass der Graph von f punktsymmetrisch zum Ursprung ist, untersuchen Sie das Verhalten von 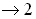 , und ermitteln Sie die Gleichungen aller Asymptoten des Graphen von f. (9 BE)
, und ermitteln Sie die Gleichungen aller Asymptoten des Graphen von f. (9 BE)
Bestimmen Sie ohne Verwendung der zweiten Ableitung die exakten Koordinaten und die Art der Extrempunkte des Graphen von f. (10 BE)
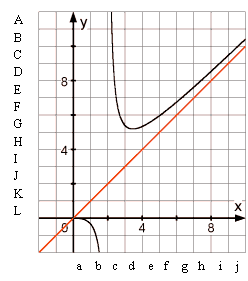
In nebenstehender Grafik sind die Winkelhalbierende des I. Quadranten sowie der Graph von f für 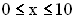 eingetragen. Ermitteln Sie aus der Grafik einen ganzzahligen Näherungswert für das Integral
eingetragen. Ermitteln Sie aus der Grafik einen ganzzahligen Näherungswert für das Integral 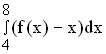 . Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate, die mit Buchstabenkombinationen bezeichnet werden. (5 BE)
. Erläutern Sie Ihre Überlegungen mit Hilfe der eingezeichneten Quadrate, die mit Buchstabenkombinationen bezeichnet werden. (5 BE)
1.4
Bestimmen Sie die reellen Parameter a und b so, dass die Funktion F mit
Sie die reellen Parameter a und b so, dass die Funktion F mit  + b·ln(x
+ b·ln(x – 4)
– 4)
(Teilergebnis: a = 0,5; b = 2)
1.5
Nun wird die Schar von Funktionen f mit f
mit f (x) =
(x) = 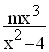 und m
und m![]() IR\{0} in der Definitionsmenge ID
IR\{0} in der Definitionsmenge ID betrachtet. Begründen Sie, welchen Einfluss der Parameter m auf den Verlauf des Graphen von
betrachtet. Begründen Sie, welchen Einfluss der Parameter m auf den Verlauf des Graphen von 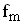 im Vergleich zum Graphen von f hat. Gehen Sie dabei auf die Fälle
im Vergleich zum Graphen von f hat. Gehen Sie dabei auf die Fälle 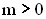 ,
, 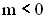 ,
, 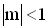 und
und 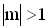 ein. Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und die Art der Extrempunkte des Graphen von f
ein. Geben Sie die Gleichungen der Asymptoten sowie die Koordinaten und die Art der Extrempunkte des Graphen von f an. (8 BE)
an. (8 BE)
Gegeben ist nun die Funktion g mit g(x) = 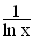 und D
und D
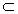 IR .
IR .
2.1
Ermitteln Sie die maximale Definitionsmenge D , und zeichnen Sie den Graphen der Logarithmusfunktion
, und zeichnen Sie den Graphen der Logarithmusfunktion 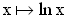 für
für 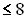 .
. sowie das Monotonieverhalten des Graphen von g. Skizzieren Sie nun auch den Graphen von g in das gleiche Koordinatensystem. (7 BE)
sowie das Monotonieverhalten des Graphen von g. Skizzieren Sie nun auch den Graphen von g in das gleiche Koordinatensystem. (7 BE)
2.2
Zeigen Sie, dass die Beziehung g(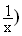 = – g(x) für alle x
= – g(x) für alle x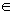 D
D richtig ist, und skizzieren Sie den Graphen von
richtig ist, und skizzieren Sie den Graphen von 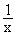 )
)
Bei Bergwanderungen kann man mit Hilfe eines Luftdruckmessgerätes den Höhenunterschied bezüglich der Startposition bestimmen. Hierbei wird die barometrische Höhenformel 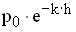
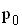 der Luftdruck am Startort (also in der Höhe 0 m), p(h) der Luftdruck nach h zurückgelegten Höhenmetern und k eine Gerätekonstante ist.
der Luftdruck am Startort (also in der Höhe 0 m), p(h) der Luftdruck nach h zurückgelegten Höhenmetern und k eine Gerätekonstante ist.
3.1
Nun sei 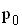 =750 hPa (=Hektopascal) und k =
=750 hPa (=Hektopascal) und k = 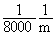 . Berechnen Sie den Luftdruck in den Höhen 100 m,
. Berechnen Sie den Luftdruck in den Höhen 100 m,
Berechnen Sie, in welcher Höhe h sich der Bergsteiger über dem Ausgangsniveau befindet, wenn das Gerät 720 hPa anzeigt. (3 BE)
3.3
Erläutern Sie, weshalb und unter welcher Einschränkung folgende Aussage gilt: Wenn in der Höhe h0 der Luftdruck p(h0) herrscht, so herrscht in der Höhe h=h0+ε annähernd der Luftdruck p(h) ≈
(Hinweis: Verwenden Sie die Tangentengleichung im Punkt P(h0| p(h0)). )
1.0
Gegeben ist die Funktion f : 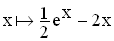 mit der Definitionsmenge
mit der Definitionsmenge 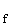 = IR.
= IR.
1.1
Untersuchen Sie das Monotonieverhalten des Graphen von f. Schließen Sie daraus auf die Art des Extrempunktes, und berechnen Sie dessen Koordinaten. (6 BE)
1.2
Zeigen Sie durch Grenzwertrechnung, dass die Gerade mit der Gleichung y = –2x Asymptote des Graphen von f für x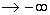 ist, und geben Sie das Verhalten von f(x) für x
ist, und geben Sie das Verhalten von f(x) für x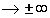 an. (5 BE)
an. (5 BE)
1.3
Begründen Sie mit den bisherigen Ergebnissen, dass f genau zwei Nullstellen besitzt. Berechnen Sie einen Näherungswert für eine Nullstelle, indem Sie zwei Schritte des Newtonverfahrens mit dem Startwert x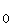 = 0 durchführen. (7 BE)
= 0 durchführen. (7 BE)
(Teilergebnis: xN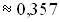 )
)
1.4
Zeichnen Sie die Asymptote und den Graphen von f unter Verwendung der bisherigen Ergebnisse sowie geeigneter Funktionswerte für –2 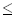 x
x 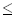 3 in ein kartesisches Koordinatensystem (1LE = 1 cm). (5 BE)
3 in ein kartesisches Koordinatensystem (1LE = 1 cm). (5 BE)
1.5
Berechnen Sie die Maßzahl der endlichen Fläche, die der Graph von f mit den Koordinatenachsen im I.Quadranten einschließt, auf 3 Dezimalen. (4 BE)
2.0
Nun ist die Funktion g mit der Funktionsgleichung g(x) = a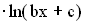
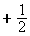 mit D
mit D
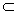 IR und
IR und 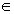 IR\{0}
IR\{0}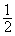 ), hat dort die Steigung 1 sowie an der Stelle x = –1 die Steigung 2.
), hat dort die Steigung 1 sowie an der Stelle x = –1 die Steigung 2.
2.1
Berechnen Sie die Koeffizienten a, b und c. (8 BE)
(Ergebnis: a = 2; b = 0,5; c = 1)
2.2
Bestimmen Sie die größtmögliche Definitionsmenge D und zeigen Sie außerdem, dass der Graph von g in D
und zeigen Sie außerdem, dass der Graph von g in D streng monoton steigt. (4 BE)
streng monoton steigt. (4 BE)
2.3
Zeigen Sie, dass die Funktion 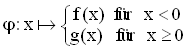 mit f aus Aufgabe 1 an der Stelle
mit f aus Aufgabe 1 an der Stelle 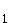 = 0
= 0 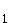 = 0 eine Minimalstelle von
= 0 eine Minimalstelle von 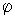 ist. (7 BE)
ist. (7 BE)
3.0
Die Bundesrepublik Deutschland hat im Jahr 2001 eine Bevölkerungszahl von 82 Millionen und eine Bevölkerungsabnahme von 0,1 % pro Jahr. Die Demokratische Republik Kongo hat im gleichen Jahr 52 Millionen Einwohner und eine Bevölkerungszunahme von 3,2 % pro Jahr. Es soll vereinfachend angenommen werden, dass sich in den nächsten 30 Jahren die Wachstumsangaben nicht verändern.
3.1
Erläutern Sie den Ansatz D(t) = D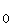
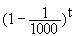 für die Bevölkerungszahl in Deutschland für
für die Bevölkerungszahl in Deutschland für 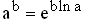 , dass sich damit näherungsweise die Beziehung D(t) =
, dass sich damit näherungsweise die Beziehung D(t) = 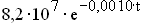 ergibt, und entwickeln Sie eine analoge Formel für die Bevölkerungszahl K(t) des Kongo. Dabei wird t = 0 im Jahr 2001 gesetzt und t in Jahren angegeben. (8 BE)
ergibt, und entwickeln Sie eine analoge Formel für die Bevölkerungszahl K(t) des Kongo. Dabei wird t = 0 im Jahr 2001 gesetzt und t in Jahren angegeben. (8 BE)
(Teilergebnis: K(t) = 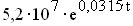 )
)
3.2
Berechnen Sie, in welchem Jahr sich die Bevölkerung des Kongo im Vergleich zum Jahr 2001 verdoppelt haben wird und in welchem Jahr die Einwohnerzahlen von Deutschland und Kongo gleich groß sein werden. (6 BE)
