1.0 | Gegeben sind die beiden Funktionen f: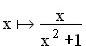 und g: und g: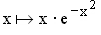 mit den Definitionsmengen D(f) = D(g) = IR . mit den Definitionsmengen D(f) = D(g) = IR . |
| |
| 1.1 | Zeigen Sie, dass die Graphen der Funktionen f und g punktsymmetrisch zum Ursprung sind und dass sie die gleiche Asymptote besitzen. (6 BE) |
| |
| 1.2 | Zeigen Sie, dass beide Graphen im Ursprung die gleiche Tangente besitzen.
(Teilergebnis: 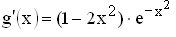 ) (7 BE) ) (7 BE) |
| |
| 1.3 | Ermitteln Sie ohne Verwendung der 2.Ableitung die Art und die Koordinaten aller Extrempunkte der beiden Graphen. (8 BE) |
| |
1.4 | Nun wird die Hilfsfunktion h mit 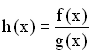 für x für x  ] 0 ; ∞ [ betrachtet. Weisen Sie nach, dass die Funktion h streng monoton steigt, und zeigen Sie, dass gilt: ] 0 ; ∞ [ betrachtet. Weisen Sie nach, dass die Funktion h streng monoton steigt, und zeigen Sie, dass gilt: 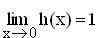 . Begründen Sie damit, dass im angegebenen Intervall der Graph von f stets oberhalb des Graphen von g verläuft. (9 BE) . Begründen Sie damit, dass im angegebenen Intervall der Graph von f stets oberhalb des Graphen von g verläuft. (9 BE) |
| |
1.5 | Zeichnen Sie die Graphen von f und g sowie deren gemeinsame Tangente unter Verwendung der bisherigen Ergebnisse für –2 ≤ x ≤ 2 in ein kartesisches Koordinatensystem. (1 LE = 2 cm) (7 BE) |
| |
1.6 | Bestimmen Sie die Konstanten k und m so, dass F mit F(x)= k · ln(x Sie die Konstanten k und m so, dass F mit F(x)= k · ln(x + 1) und G mit G(x) = + 1) und G mit G(x) = 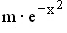 Stammfunktionen von f und g sind. Berechnen Sie damit, um wieviel Prozent das Integral Stammfunktionen von f und g sind. Berechnen Sie damit, um wieviel Prozent das Integral 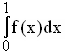 größer als größer als 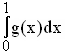 ist. ist.
( Zur Kontrolle: k = 0,5 ; m = –0,5 ) (10 BE) |
| |
| |
2.0 | In nebenstehender Graphik sind die Graphen folgender Funktionen dargestellt:
k1: y = ex, k2: y = ln (x) und k3: y = –x + (e + 1). | 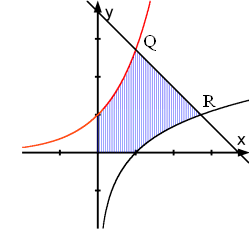 |
| |
2.1 | Begründen Sie, dass die schraffierte Fläche achsensymmetrisch ist. (4 BE) |
| |
2.2 | Zeigen Sie, dass der Eckpunkt Q die Abszisse x = 1 besitzt und bestimmen Sie die exakten Koordinaten des Eckpunktes R. Berechnen Sie den Inhalt der schraffierten Fläche. (9 BE) |
| |

|
1.0 | Gegeben ist die Funktion 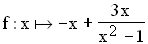 mit der Definitionsmenge D(f) mit der Definitionsmenge D(f) 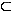 IR. IR. |
| |
1.1 | Bestimmen Sie die maximale Definitionsmenge D(f) und die Nullstellen, und zeigen Sie, dass der Graph von f punktsymmetrisch zum Ursprung ist. (7 BE) |
| |
1.2 | Untersuchen Sie das Verhalten von f(x) für x  ± 1 und geben Sie die Gleichungen aller Asymptoten des Graphen von f an. (6 BE) ± 1 und geben Sie die Gleichungen aller Asymptoten des Graphen von f an. (6 BE) |
| |
1.3 | Ermitteln Sie das Monotonieverhalten des Graphen von f, und zeichnen Sie den Graphen von f und alle Asymptoten unter Verwendung der bisherigen Ergebnisse für |x| ≤ 6 in ein kartesisches Koordinatensystem. (1 LE = 1 cm) (10 BE) |
| |
1.4 | Berechnen Sie, für welche Werte x mit x > 1 die Abweichung der Funktionswerte f(x) von der Geraden y = –x weniger als 0,5 beträgt. (6 BE) |
| |
1.5 | Zeigen Sie, dass 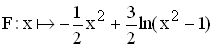 für x > 1 eine Stammfunktion von f ist. Berechnen Sie dann den Inhalt der Fläche, die der Graph von f und die Geraden mit den Gleichungen x = 2, x = 6 und y = –x einschließen. (7 BE) für x > 1 eine Stammfunktion von f ist. Berechnen Sie dann den Inhalt der Fläche, die der Graph von f und die Geraden mit den Gleichungen x = 2, x = 6 und y = –x einschließen. (7 BE) |
| |
| |
2.0 | Für die Abkühlung einer heißen Flüssigkeit gilt das Newtonsche Abkühlungsgesetz T(t) = T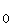 + (T + (T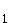 – T – T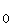 )·e-kt. Hierbei ist )·e-kt. Hierbei ist
T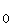 die Maßzahl der konstanten Umgebungstemperatur (in oC), die Maßzahl der konstanten Umgebungstemperatur (in oC),
T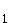 die Maßzahl der anfänglichen Temperatur (in oC) der Flüssigkeit, die Maßzahl der anfänglichen Temperatur (in oC) der Flüssigkeit,
T(t) die Maßzahl der momentanen Temperatur (in oC) und
t die Maßzahl der Zeit in Sekunden (t ≥ 0).
Bei einer Umgebungstemperatur von 20oC hat sich die Flüssigkeit von anfangs 80oC nach 60 Sekunden auf 54,5oC abgekühlt. Auf Benennungen wird bei der Rechnung verzichtet, bei den Antwortsätzen sollen sie enthalten sein. |
| |
2.1 | Berechnen Sie hieraus die Maßzahl von k, den Wert der Ableitung T '(0) und den Grenzwert Sie hieraus die Maßzahl von k, den Wert der Ableitung T '(0) und den Grenzwert 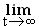 T(t), und interpretieren Sie die beiden letzten Ergebnisse im Sinn des vorliegenden Sachverhalts. T(t), und interpretieren Sie die beiden letzten Ergebnisse im Sinn des vorliegenden Sachverhalts.
(Teilergebnis: k ≈ 0,0092) (10 BE) |
| |
2.2 | Nach welcher Zeit ist die Temperatur um 55 oC gesunken? (4 BE) |
| |
| |
3. | Der Graph einer Funktion 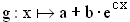 mit a, b, c, x mit a, b, c, x  IR soll folgende drei Bedingungen erfüllen: Er schneidet die x-Achse bei x = 2 und die y-Achse bei y = –3. Außerdem soll er für x IR soll folgende drei Bedingungen erfüllen: Er schneidet die x-Achse bei x = 2 und die y-Achse bei y = –3. Außerdem soll er für x  –∞ die waagrechte Asymptote y = 1 besitzen. Begründen Sie, dass diese Bedingungen nicht gleichzeitig zu erfüllen sind. Wie müsste die erste der drei Bedingungen abgeändert werden, damit eine solche Funktion g existiert? Bestimmen Sie für eine geeignete Nullstelle Ihrer Wahl die Parameterwerte a, b und c. (10 BE) –∞ die waagrechte Asymptote y = 1 besitzen. Begründen Sie, dass diese Bedingungen nicht gleichzeitig zu erfüllen sind. Wie müsste die erste der drei Bedingungen abgeändert werden, damit eine solche Funktion g existiert? Bestimmen Sie für eine geeignete Nullstelle Ihrer Wahl die Parameterwerte a, b und c. (10 BE)

|
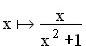 und g:
und g: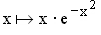 mit den Definitionsmengen
mit den Definitionsmengen 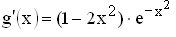 ) (7 BE)
) (7 BE)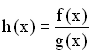 für x
für x  ] 0 ; ∞ [ betrachtet. Weisen Sie nach, dass die Funktion h streng monoton steigt, und zeigen Sie, dass gilt:
] 0 ; ∞ [ betrachtet. Weisen Sie nach, dass die Funktion h streng monoton steigt, und zeigen Sie, dass gilt: 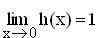 . Begründen Sie damit, dass im angegebenen Intervall der Graph von f stets oberhalb des Graphen von g verläuft. (9 BE)
. Begründen Sie damit, dass im angegebenen Intervall der Graph von f stets oberhalb des Graphen von g verläuft. (9 BE) Sie die Konstanten k und m so, dass F mit F(x)= k · ln(x
Sie die Konstanten k und m so, dass F mit F(x)= k · ln(x + 1) und G mit
+ 1) und G mit 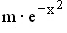
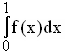 größer als
größer als 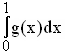 ist.
ist.

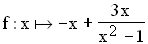 mit der Definitionsmenge
mit der Definitionsmenge 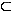 IR.
IR. ± 1 und geben Sie die Gleichungen aller Asymptoten des Graphen von f an. (6 BE)
± 1 und geben Sie die Gleichungen aller Asymptoten des Graphen von f an. (6 BE)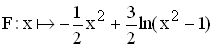 für x > 1 eine Stammfunktion von f ist. Berechnen Sie dann den Inhalt der Fläche, die der Graph von f und die Geraden mit den Gleichungen
für x > 1 eine Stammfunktion von f ist. Berechnen Sie dann den Inhalt der Fläche, die der Graph von f und die Geraden mit den Gleichungen 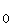 + (T
+ (T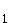 – T
– T Sie hieraus die Maßzahl von k, den Wert der Ableitung T '(0) und den Grenzwert
Sie hieraus die Maßzahl von k, den Wert der Ableitung T '(0) und den Grenzwert 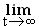 T(t), und interpretieren Sie die beiden letzten Ergebnisse im Sinn des vorliegenden Sachverhalts.
T(t), und interpretieren Sie die beiden letzten Ergebnisse im Sinn des vorliegenden Sachverhalts.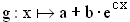 mit a, b, c, x
mit a, b, c, x