1.0 | Gegeben ist die Funktion g: x 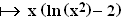 mit der Definitionsmenge D(g) = IR\{0}. Ihr Graph sei G(g). mit der Definitionsmenge D(g) = IR\{0}. Ihr Graph sei G(g). |
| |
| 1.1 | Untersuchen Sie G(g) auf Symmetrie und berechnen Sie die Nullstellen von g. (4 BE) |
| |
| 1.2 | Geben Sie die Art der Definitionslücke x = 0 an und begründen Sie Ihre Angabe. (4 BE) |
| |
| 1.3 | Bestimmen Sie Art und Koordinaten der Extrempunkte des Graphen von g.
(Zur Kontrolle: g '(x) = ln(x2) ) (6 BE) |
| |
1.4 | Zeichnen Sie den Graphen von g für –3 ≤ x ≤ 3 unter Verwendung aller bisherigen Ergebnisse in ein kartesisches Koordinatensystem. (1 LE = 1 cm) (5 BE) |
| |
1.5 | Ermitteln Sie die reellen Werte von a und b, für welche die Funktion 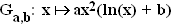 mit mit 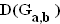 = ]0 ; +∞[ eine Stammfunktion der Funktion g ist. = ]0 ; +∞[ eine Stammfunktion der Funktion g ist.
(Ergebnis: a = 1 ; b = –1,5 ) (4 BE) |
| |
1.6 | Die x-Achse, die Gerade mit der Gleichung x = 1 und der Graph von g begrenzen für x ≥ 1 im vierten Quadranten ein Flächenstück. Berechnen Sie dessen Flächenmaßzahl A. (5 BE) |
| |
| |
2.0 | Gegeben ist die Schar reeller Funktionen 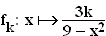 mit maximaler Definitionsmenge mit maximaler Definitionsmenge 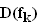 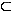 IR sowie k IR sowie k  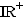 . Der Graph von . Der Graph von 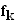 heißt heißt 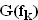 . . |
| |
2.1 | Bestimmen Sie 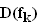 und zeigen Sie, dass der Graph und zeigen Sie, dass der Graph 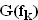 symmetrisch zur y-Achse verläuft. (3 BE) symmetrisch zur y-Achse verläuft. (3 BE) |
| |
2.2 | Untersuchen Sie das Verhalten von 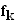 (x) in der Umgebung der Definitionslücken und geben Sie die Gleichungen aller Asymptoten von (x) in der Umgebung der Definitionslücken und geben Sie die Gleichungen aller Asymptoten von 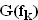 an. (5 BE) an. (5 BE) |
| |
2.3 | Ermitteln Sie das Intervall I der x-Werte, in dem der Graph 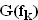 oberhalb der x-Achse verläuft. (4 BE) oberhalb der x-Achse verläuft. (4 BE) |
| |
2.4 | Geben Sie die maximalen Monotonieintervalle von 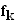 an und bestimmen Sie damit die Art und die Koordinaten des Extrempunktes des Graphen an und bestimmen Sie damit die Art und die Koordinaten des Extrempunktes des Graphen 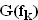 in Abhängigkeit von k. in Abhängigkeit von k.
(Zur Kontrolle: 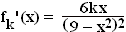 ) (7 BE) ) (7 BE) |
| | 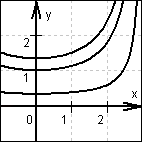 |
2.5 | In der nebenstehenden Zeichnung sind die Graphen 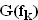 für einige ganzzahlige Werte von k teilweise dargestellt. Bestimmen Sie aufgrund der bisherigen Ergebnisse, für welche Werte von k die Graphen dargestellt sind. (4 BE) für einige ganzzahlige Werte von k teilweise dargestellt. Bestimmen Sie aufgrund der bisherigen Ergebnisse, für welche Werte von k die Graphen dargestellt sind. (4 BE) |
| |
| |
3.0 | Ein zylindrisches Gefäß ist mit Schaum gefüllt. Ist h(t) die Schaumhöhe zu einem Zeitpunkt t (t ≥ 0), so gilt für den Zerfall des Schaums folgendes Gesetz : h(t) = h0e–ct, wobei h0 die Schaumhöhe zu Beginn und c eine für den Schaum charakteristische konstante Größe ist. Bei der Rechnung kann auf die Verwendung von Einheiten verzichtet werden. |
| |
3.1 | Zum Zeitpunkt t1 = 2,0 min beträgt die Schaumhöhe 8,0 cm, zum Zeitpunkt t2 = 7,0 min beträgt die Schaumhöhe 3,0 cm. Ermitteln Sie die Werte der Konstanten h0 und c.
(Ergebnis: h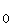 ≈ 12 cm ; c ≈ 0,20 ≈ 12 cm ; c ≈ 0,20 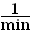 ) (6 BE) ) (6 BE) |
| |
3.2 | Berechnen Sie den Zeitpunkt t3 , zu dem sich die Schaumhöhe halbiert hat. (3 BE) |
| |
| |

|
1.0 | Gegeben ist die Funktion 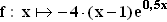 mit der Definitionsmenge D(f) = IR. mit der Definitionsmenge D(f) = IR. |
| |
1.1 | Geben Sie die Nullstelle von f an. Untersuchen Sie das Verhalten von f(x) für x  ±∞ und geben Sie die Gleichung der Asymptote von G(f) an. (6 BE) ±∞ und geben Sie die Gleichung der Asymptote von G(f) an. (6 BE) |
| |
1.2 | Ermitteln Sie die maximalen Monotonieintervalle von f sowie die Art und die Koordinaten des lokalen Extrempunktes von G(f) und geben Sie die Wertemenge W(f) von f an.
(Teilergebnis: 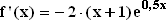 ) (8 BE) ) (8 BE) |
| |
1.3 | Zeichnen Sie G(f) unter Verwendung der bisherigen Ergebnisse für –8 ≤ x ≤ 1,5 in ein kartesisches Koordinatensystem. (5 BE) |
| |
1.4.0 | Gegeben ist nun die Funktion 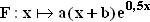 mit D(F) = IR und a, b mit D(F) = IR und a, b  IR. IR. |
1.4.1 | Berechnen Sie die Koeffizienten a und b so, dass F eine Stammfunktion von f ist.
(Ergebnis: a = –8; b = –3 ) (4 BE) |
1.4.2 | Der Graph G(f), die x-Achse und die Gerade mit der Gleichung x = k mit k < 0 begrenzen eine Fläche A. Berechnen Sie die Maßzahl A in Abhängigkeit von k. Untersuchen Sie, ob 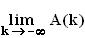 existiert und geben Sie gegebenenfalls den Wert an. (7 BE) existiert und geben Sie gegebenenfalls den Wert an. (7 BE) |
| |
| |
2.0 | In der nebenstehenden Zeichnung ist der Graph einer gebrochen-rationalen Funktion 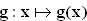 mit D(g) = IR \ {–2; 2} abgebildet. Der Graph ist achsensymmetrisch zur y-Achse. Alle weiteren Eigenschaften können der Zeichnung entnommen werden. mit D(g) = IR \ {–2; 2} abgebildet. Der Graph ist achsensymmetrisch zur y-Achse. Alle weiteren Eigenschaften können der Zeichnung entnommen werden. | 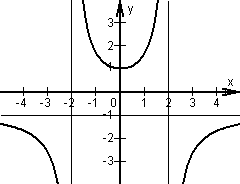 |
| |
2.1 | Bestimmen Sie einen Funktionsterm g(x), wenn Zähler und Nenner jeweils Polynome zweiten Grades sind. (6 BE) |
| |
2.2 | Stellen Sie fest, ob Zähler und Nenner von g(x) auch jeweils Polynome der Form ax3 + bx (a  IR\{0}, b IR\{0}, b  IR) sein können, und begründen Sie Ihre Aussage. (4 BE) IR) sein können, und begründen Sie Ihre Aussage. (4 BE) |
| |
| |
3.0 | Ein Opa möchte seinen Enkel finanziell absichern. Er bietet dem Enkel zwei Alternativen an: Entweder gibt er ihm jeden Monat 50  in bar oder er legt bei einer Bank 2000 in bar oder er legt bei einer Bank 2000 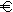 an, die zu 7,25 % jährlich verzinst werden. an, die zu 7,25 % jährlich verzinst werden. |
| |
3.1 | Für die Bankalternative gilt für das Kapital nach t Jahren (t ≥ 0) die Zinsformel K(t) = K0 (1 + 0,0725)t. Zeigen Sie unter Verwendung der Formel a = eln a, dass sich näherungsweise die Beziehung K(t) = 2000·e0,07 t ergibt. (3 BE) |
| |
3.2 | Stellen Sie eine Funktionsgleichung für die Funktion G auf, die den Geldbetrag beschreibt, der sich nach Opas anderer Alternative nach t Jahren ansammelt. (2 BE) |
| |
3.3 | Zeichnen Sie die Graphen der beiden Funktionen K und G für 0 ≤ t ≤ 20 in ein Koordinatensystem.
(Maßstab: x-Achse: 1 cm 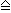 4 Jahre; y-Achse: 1 cm 4 Jahre; y-Achse: 1 cm 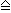 2000 2000 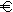 ) (5 BE) ) (5 BE) |
| |
3.4 | Geben Sie die Anzahl der Zeitpunkte an, zu denen bei beiden Alternativen das gleiche Kapital angesammelt ist, und erläutern Sie Ihre Aussage. Ermitteln Sie jeweils ein Zeitintervall der Länge 1 Jahr, in dem diese Zeitpunkte liegen. Verwenden Sie zur Lösung eine geeignete Wertetabelle. (7 BE) |
| |
3.5 | Beurteilen Sie vergleichend die beiden Anlagearten. (3 BE)

|
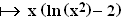 mit der Definitionsmenge
mit der Definitionsmenge 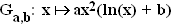 mit
mit 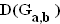 = ]0 ; +∞[
= ]0 ; +∞[ 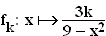 mit maximaler Definitionsmenge
mit maximaler Definitionsmenge 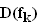
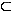 IR sowie k
IR sowie k 
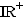 . Der Graph von
. Der Graph von 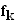 heißt
heißt 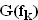 .
.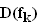 und zeigen Sie, dass der Graph
und zeigen Sie, dass der Graph 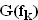 symmetrisch zur y-Achse verläuft. (3 BE)
symmetrisch zur y-Achse verläuft. (3 BE)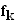 (x) in der Umgebung der Definitionslücken und geben Sie die Gleichungen aller Asymptoten von
(x) in der Umgebung der Definitionslücken und geben Sie die Gleichungen aller Asymptoten von 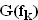 an. (5 BE)
an. (5 BE)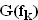 oberhalb der x-Achse verläuft. (4 BE)
oberhalb der x-Achse verläuft. (4 BE)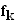 an und bestimmen Sie damit die Art und die Koordinaten des Extrempunktes des Graphen
an und bestimmen Sie damit die Art und die Koordinaten des Extrempunktes des Graphen 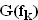 in Abhängigkeit von k.
in Abhängigkeit von k.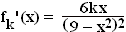 ) (7 BE)
) (7 BE)
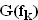 für einige ganzzahlige Werte von k teilweise dargestellt. Bestimmen Sie aufgrund der bisherigen Ergebnisse, für welche Werte von k die Graphen dargestellt sind. (4 BE)
für einige ganzzahlige Werte von k teilweise dargestellt. Bestimmen Sie aufgrund der bisherigen Ergebnisse, für welche Werte von k die Graphen dargestellt sind. (4 BE) ≈ 12 cm ; c ≈ 0,20
≈ 12 cm ; c ≈ 0,20 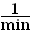 ) (6 BE)
) (6 BE)
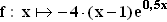 mit der Definitionsmenge
mit der Definitionsmenge  ±∞ und geben Sie die Gleichung der Asymptote von G(f) an. (6 BE)
±∞ und geben Sie die Gleichung der Asymptote von G(f) an. (6 BE)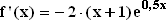 ) (8 BE)
) (8 BE)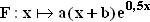 mit D(F) = IR und
mit D(F) = IR und 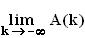 existiert und geben Sie gegebenenfalls den Wert an. (7 BE)
existiert und geben Sie gegebenenfalls den Wert an. (7 BE) mit D(g) =
mit D(g) = 
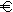 in bar oder er legt bei einer Bank 2000
in bar oder er legt bei einer Bank 2000  4 Jahre; y-Achse: 1 cm
4 Jahre; y-Achse: 1 cm