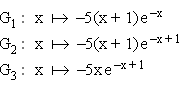1.0 | Gegeben ist die Funktion  Ihr Graph ist G(f). Ihr Graph ist G(f). |
| |
| 1.1 | Geben Sie D(f) an und untersuchen Sie f auf Nullstellen. (2 BE) |
| |
1.2 | Zeigen Sie, dass gilt: 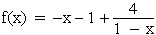 , und geben Sie die Gleichungen aller Asymptoten des Graphen G(f) an. (3 BE) , und geben Sie die Gleichungen aller Asymptoten des Graphen G(f) an. (3 BE) |
| |
| 1.3 | Bestimmen Sie die maximalen Monotonieintervalle von f , ermitteln Sie die Koordinaten und die Art der Extrempunkte von G(f), und geben Sie die Wertemenge W(f) von f an.
(Zur Kontrolle: 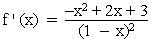 ) (10 BE) ) (10 BE) |
| |
1.4 | Zeichnen Sie G(f) und seine Asymptoten für 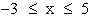 unter Verwendung der bisherigen Ergebnisse sowie der Berechnung geeigneter Funktionswerte in ein kartesisches Koordinatensystem. (L.E. 1 cm) (6 BE) unter Verwendung der bisherigen Ergebnisse sowie der Berechnung geeigneter Funktionswerte in ein kartesisches Koordinatensystem. (L.E. 1 cm) (6 BE) |
| |
1.5 | Berechnen Sie die Flächenmaßzahl A des endlichen Flächenstücks, das die y-Achse, G(f) und die Winkelhalbierende des zweiten Quadranten einschließen. (8 BE) |
| |
| |
2.0 | Gegeben ist die Schar reeller Funktionen 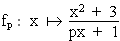 mit mit 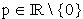 und der Definitionsmenge und der Definitionsmenge 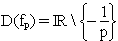 . . |
| |
2.1 | Untersuchen Sie, ob jeder Funktionsgraph der Schar fp zwei Extrempunkte besitzt. (7 BE) |
| |
2.2 | Geben Sie an, welcher der unten dargestellten Funktionsgraphen nicht zu den Graphen der Schar fp gehören kann, und begründen Sie Ihre Angabe. (3 BE)
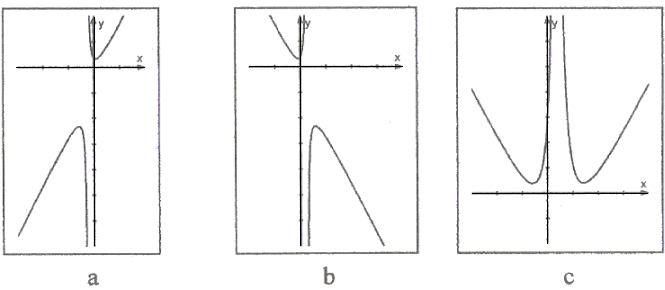 |
| |
| |
3.0 | Für das durchschnittliche Körpergewicht M (in Kilogramm) der Individuen einer bestimmten Säugetierart im Alter t (in Jahren) wird das folgende mathematische Modell zugrunde gelegt:
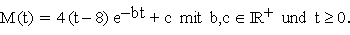
Bei Berechnungen kann auf Einheiten verzichtet werden, Ergebnisse sind gegebenenfalls auf eine Nachkommastelle zu runden. |
| |
3.1 | Ermitteln Sie die Werte der reellen Parameter b und c für den Fall, dass die Tiere im Alter von 13,0 Jahren ihr Maximalgewicht von 36,5 kg erreichen. (9 BE) |
| |
3.2.0 | Für die folgenden Teilaufgaben soll gelten: 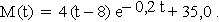 |
3.2.1 | Berechnen Sie das durchschnittliche Geburtsgewicht dieser Säugetiere. (2 BE) |
3.2.2 | Ermitteln Sie das Alter, in dem die größte Gewichtsabnahme zu erwarten ist. (6 BE) |
3.2.3 | Bestimmen Sie den Grenzwert der Funktion M für 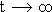 und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (4 BE) und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (4 BE) |
| |
| |

|
1.0 | Gegeben ist die Funktion 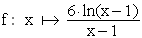 mit der maximalen Definitionsmenge D(f) mit der maximalen Definitionsmenge D(f) 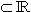 . Ihr Graph ist G(f). . Ihr Graph ist G(f). |
| |
1.1 | Bestimmen Sie D(f) und die Nullstelle von f. (3 BE) |
| |
1.2 | Untersuchen Sie das Verhalten von f(x) an den Rändern von D(f) und geben Sie die Gleichungen aller Asymptoten von G(f) an. (5 BE) |
| |
1.3 | Bestimmen Sie die Art und die Koordinaten des Extrempunktes von G(f).
(Zur Kontrolle: 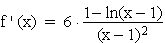 ) (8 BE) ) (8 BE) |
| |
1.4 | Bestimmen Sie die Gleichung der Tangente t an G(f) im Punkt P(2 | f(2)). (3 BE) |
| |
1.5 | Zeichnen Sie die Tangente t, die Asymptoten von G(f) und G(f) unter der Verwendung der bisherigen Ergebnisse sowie der Berechnung geeigneter Funktionswerte für 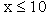 in ein kartesisches Koordinatensystem. (6 BE) in ein kartesisches Koordinatensystem. (6 BE) |
| |
1.6 | Zeigen Sie, dass die Funktion 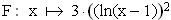 mit D(F) = D(f) eine Stammfunktion von f ist, und berechnen Sie die Flächenmaßzahl A der endlichen Fläche, die G(f), die Gerade mit der Gleichung mit D(F) = D(f) eine Stammfunktion von f ist, und berechnen Sie die Flächenmaßzahl A der endlichen Fläche, die G(f), die Gerade mit der Gleichung 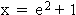 und die x-Achse einschließen. (7 BE) und die x-Achse einschließen. (7 BE) |
1.7 | Gegeben ist die Funktion 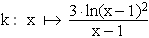 mit der maximalen Definitionsmenge D(k) mit der maximalen Definitionsmenge D(k) 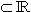 . .
Geben Sie D(k) an und beschreiben Sie den Graphen von k mit Hilfe des Graphen G(f) von f. (6 BE) |
| |
| | | 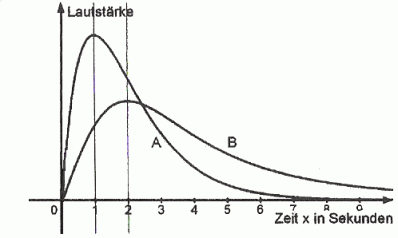 |
2.0 | In der Fernsehsendung „Wetten, dass . . . “ wird die Lautstärke des Applauses des Saalpublikums als Maß für die Beliebtheit der Saalwetten gewertet. Der Verlauf zweier „Applauskurven“ für die Wetten A und B ist in der nebenstehenden Grafik wieder- gegeben. |
| |
2.1 | Vergleichen Sie den Verlauf der beiden Kurven im Sinne der vorliegenden Thematik. (4 BE) |
| |
2.2 | Eine der beiden Kurven entspricht dem Graphen der Funktion 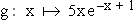 für für 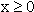 . Bestimmen Sie die Extremstelle von g und entscheiden Sie damit, welche der beiden Kurven (A oder B) der Graph von g ist. (4 BE) . Bestimmen Sie die Extremstelle von g und entscheiden Sie damit, welche der beiden Kurven (A oder B) der Graph von g ist. (4 BE) |
| |
2.3 | Die andere Kurve wird für 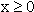 durch den Graphen einer der Funktionen durch den Graphen einer der Funktionen 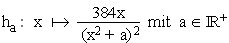 beschrieben. Bestimmen Sie den Wert von a mit Hilfe der Zeichnung. beschrieben. Bestimmen Sie den Wert von a mit Hilfe der Zeichnung.
(Ergebnis: a = 12) (5 BE) |
2.4 | Die Beliebtheit der Saalwetten kann durch den Wert des Integrals 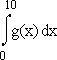 bzw. bzw. 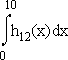 ausgedrückt werden, wobei ein größerer Wert größere Beliebtheit anzeigt. ausgedrückt werden, wobei ein größerer Wert größere Beliebtheit anzeigt. 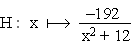 ist für ist für 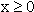 eine Stammfunktion von eine Stammfunktion von 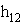 . (Nachweis nicht erforderlich) . (Nachweis nicht erforderlich)
Entscheiden Sie, welche der folgenden Funktionen für Sie, welche der folgenden Funktionen für 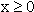 eine Stammfunktion von g ist, und begründen Sie Ihre Aussage. eine Stammfunktion von g ist, und begründen Sie Ihre Aussage.
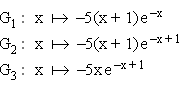
Vergleichen Sie nun die Beliebtheit der Wetten anhand der jeweiligen Integralwerte. (9 BE)

|
 Ihr Graph ist
Ihr Graph ist 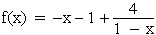 , und geben Sie die Gleichungen aller Asymptoten des Graphen G(f) an. (3 BE)
, und geben Sie die Gleichungen aller Asymptoten des Graphen G(f) an. (3 BE)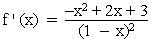 ) (10 BE)
) (10 BE)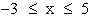 unter Verwendung der bisherigen Ergebnisse sowie der Berechnung geeigneter Funktionswerte in ein kartesisches Koordinatensystem. (L.E. 1 cm) (6 BE)
unter Verwendung der bisherigen Ergebnisse sowie der Berechnung geeigneter Funktionswerte in ein kartesisches Koordinatensystem. (L.E. 1 cm) (6 BE)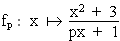 mit
mit 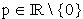 und der Definitionsmenge
und der Definitionsmenge 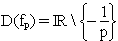 .
.
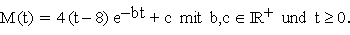
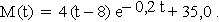
 und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (4 BE)
und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (4 BE)
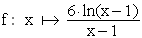 mit der maximalen Definitionsmenge D(f)
mit der maximalen Definitionsmenge D(f) 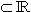 . Ihr Graph ist G(f).
. Ihr Graph ist G(f).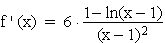 ) (8 BE)
) (8 BE)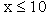 in ein kartesisches Koordinatensystem. (6 BE)
in ein kartesisches Koordinatensystem. (6 BE)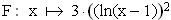 mit D(F) = D(f) eine Stammfunktion von f ist, und berechnen Sie die Flächenmaßzahl A der endlichen Fläche, die G(f), die Gerade mit der Gleichung
mit D(F) = D(f) eine Stammfunktion von f ist, und berechnen Sie die Flächenmaßzahl A der endlichen Fläche, die G(f), die Gerade mit der Gleichung 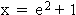 und die x-Achse einschließen. (7 BE)
und die x-Achse einschließen. (7 BE)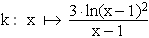 mit der maximalen Definitionsmenge D(k)
mit der maximalen Definitionsmenge D(k) 
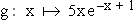 für
für 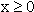 . Bestimmen Sie die Extremstelle von g und entscheiden Sie damit, welche der beiden Kurven (A oder B) der Graph von g ist. (4 BE)
. Bestimmen Sie die Extremstelle von g und entscheiden Sie damit, welche der beiden Kurven (A oder B) der Graph von g ist. (4 BE)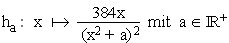 beschrieben. Bestimmen Sie den Wert von a mit Hilfe der Zeichnung.
beschrieben. Bestimmen Sie den Wert von a mit Hilfe der Zeichnung.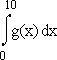 bzw.
bzw. 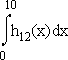 ausgedrückt werden, wobei ein größerer Wert größere Beliebtheit anzeigt.
ausgedrückt werden, wobei ein größerer Wert größere Beliebtheit anzeigt. 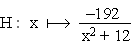 ist für
ist für  . (Nachweis nicht erforderlich)
. (Nachweis nicht erforderlich) Sie, welche der folgenden Funktionen für
Sie, welche der folgenden Funktionen für