1.0
Gegeben ist die Funktion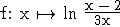 
mit der
maximalen Definitionsmenge 
.
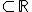Zeigen Sie, dass gilt: D(f) = IR \ [0;2]. Untersuchen Sie das Verhalten von f(x) an den Rändern von D(f), geben Sie die Gleichungen aller Asymptoten von G(f) an und berechnen Sie die Nullstelle von f. (10 BE)
Bestimmen Sie das Monotonieverhalten von
f .
(Teilergebnis: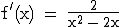 
) (5 BE)
1.3
Zeichnen Sie G(f) unter Verwendung der bisherigen Ergebnisse und nach Berechnung geeigneter Funktionswerte für –5 ≤ x ≤ 7 in ein kartesisches Koordinatensystem. (1 LE = 1 cm) (5 BE)
1.4
Die Funktion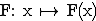 
mit D(F) = D(f) ist eine Stammfunktion
von f. Ermitteln Sie unter Verwendung bisheriger Ergebnisse die Abszisse
und die Art des Extrempunktes und das Krümmungsverhalten des Graphen von
F. (6 BE)
2.0
Gegeben ist die Funktion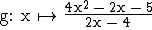 
mit der maximalen Definitionsmenge
.
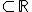2.1
Geben Sie D(g) an und bestimmen Sie das Verhalten von g(x) in der Umgebung der Definitionslücke. Ermitteln Sie die Gleichungen und die jeweilige Art aller Asymptoten von G(g). (7 BE)
2.2
Ermitteln Sie die Menge B der x-Werte, für welche G(g) oberhalb der Geraden k mit der Gleichung y = 2x + 3 verläuft. (3 BE)
2.3
Berechnen Sie die Flächenmaßzahl A(b) der
Fläche, die von G(g), der Geraden k und den Geraden mit den
Gleichungen x = 4 und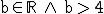 
eingeschlossen wird. Untersuchen Sie, ob
A(b) für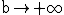 
gegen einen endlichen Wert strebt.
3.0
Die Anzahl p der Pilze in einer Kultur in
Abhängigkeit von der Zeit t in Stunden wird für t ≥
0 durch den Funktionsterm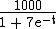 
3.1
Bestimmen Sie die Anzahl der Pilze zum Zeitpunkt t = 0 und nach sehr langer Beobachtungszeit. Berechnen Sie den Zeitpunkt t1, zu dem die Pilzkultur 875 Pilze enthält. (5 BE)
3.2
Nun wird die Ableitungsfunktion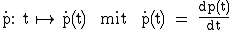 
und t ≥ 0 betrachtet. Interpretieren
Sie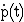 
im gegebenen Sachzusammenhang und zeigen Sie, dass
die Anzahl der Pilze im gesamten Beobachtungszeitraum echt monoton
zunimmt.
(Teilergebnis: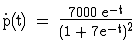 
) (5 BE)
3.3
Ohne Nachweis kann im Folgenden verwendet werden,
dass 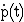für t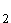
= ln
7 seinen maximalen Wert annimmt. Zeichnen Sie den Graphen von
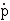für 0 ≤ t ≤ 6 unter Verwendung der
bisherigen Ergebnisse und der Berechnung weiterer geeigneter
Funktionswerte in ein Koordinatensystem.
(Maßstab: t-Achse: 1h
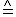2cm ; 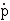-Achse: 100 Pilze / h 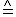1cm ) (5 BE)
3.4
Zeichnen Sie unter Verwendung der Eigenschaften des
Graphen von 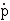den Graphen von p in das
Koordinatensystem von Teilaufgabe 3.3.
(Maßstab: t-Achse: 1h 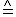2cm ; p-Achse: 100 Pilze 1cm ) (3 BE)
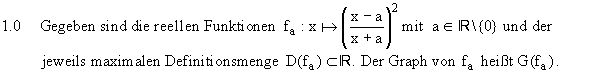1.1 Geben Sie D(fa) an und untersuchen Sie das Verhalten von fa(x) in der Umgebung der
Definitionslücke. Geben Sie die Nullstelle von fa an und beschreiben Sie den Verlauf
von G(fa) in der Umgebung der Nullstelle. (6 BE)
1.2 Bestimmen Sie die Wertemenge W(fa) von fa . (3 BE)
1.3 Zeigen Sie, dass alle Graphen G(fa) die y-Achse im gleichen Punkt T schneiden und
ermitteln Sie in Abhängigkeit von a eine Gleichung der Tangente an G(fa) in diesem
Punkt T.
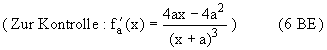Im Folgenden sei a = 2 . Die Funktion f2 wird kurz mit f, ihre Definitionsmenge mit D(f) und
ihr Graph mit G(f) bezeichnet.
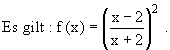1.4 Ermitteln Sie - möglichst einfach - die Art und die Koordinaten des Extrempunktes
von G(f). (4 BE)
1.5 Geben Sie die Gleichungen aller Asymptoten von G(f) an und berechnen Sie
f(-3,75), f(-1) und f(0). Zeichnen Sie die Asymptoten und G(f) nach Berechnung weiterer
geeigneter Funktionswerte für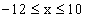 
in ein kartesisches Koordinatensystem.
( 1 LE = 0,5 cm ) (7 BE)
1.6 Untersuchen Sie ohne Verwendung der zweiten Ableitung von f, ob G(f) für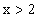 
einen Wendepunkt besitzt. (3 BE)
1.7 Die Funktion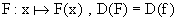 
ist eine Stammfunktion von f. Geben Sie
die Abszisse des Punktes an, in dem der Graph von F eine waagrechte Tangente besitzt
und bestimmen Sie die besondere Art dieses Punktes. (3 BE)
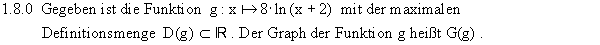1.8.1 Geben Sie D(g) an und untersuchen Sie das Verhalten von g(x) an den Rändern
der Definitionsmenge D(g). (5 BE)
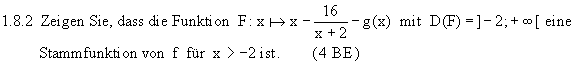1.8.3 Der Graph G(f) und die Geraden mit den Gleichungen y = 1 und x = 6 begrenzen
im ersten Quadranten eine Fläche. Schraffieren Sie diese Fläche in der Graphik von
Aufgabe 1.5 und berechnen Sie die Maßzahl A des Flächeninhalts dieser Fläche. (5 BE)
2.0 Unter natürlicher Radioaktivität versteht man die Eigenschaft von bestimmten
Atomkernen, sich unter Aussendung von Strahlen umzuwandeln bzw. zu zerfallen.
Die Größe, die diese Umwandlung beschreibt, ist die Aktivität A(t). Sie gibt die Anzahl
der radioaktiven Zerfälle pro Minute zu einer bestimmten Zeit t an.
Die Aktivität ändert sich im Laufe der Zeit nach folgendem Gesetz :
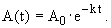Die Zeit t 
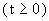wird in Jahren angegeben, A0 ist die Aktivität zur Zeit t = 0 und k ist
die sogenannte Zerfallskonstante.
Für alle folgenden Aufgaben wird der radioaktive Kern des Kohlenstoffs C14 untersucht.
Bei Berechnungen kann auf die Verwendung von Einheiten verzichtet werden.
2.1 Zur Zeit t1 = 550 Jahre beträgt die Aktivität 
, zur Zeit t2 = 1162 Jahre
beträgt die Aktivität 
. Ermiteln Sie die Werte von A0 und k .
(6 BE)
2.2 Im Jahre 1947 wurden in einer zerfallenen Tempelruine am Toten Meer die berühmten
"Qumran Papyrus-Rollen" gefunden, die Aufschluss über die Authentizität des
Alten Testaments gaben.
Um deren Echtheit zu prüfen, wurde die sogenannte "C14-Methode" angewandt.
Dabei wird ausgenutzt, dass jeder lebende Organismus unter anderem radioaktive
C14-Atome aus der Luft aufnimmt, wobei deren Anteil über Jahrtausende als konstant
betrachtet wird. Sobald ein Organismus stirbt, endet die Aufnahme von C14-Atomen.
Der in dem toten Organismus vorhandene Kohlenstoff C14 zerfällt nach dem
unter 2.0 bzw. 2.1 formulierten Gesetz.
Im Jahre 1947 ergab die Untersuchung einer Probe dieser Papyrus-Rollen, dass diese
nur noch 79% der Aktivität A0 besaß, die an lebenden Organismen festzustellen ist.
Berechnen Sie, vor wie vielen Jahren ungefähr die Papyrusstauden geerntet wurden,
die zur Herstellung der Qumran-Rollen verwendet wurden. ( 4 BE)
2.3 Bekannter als die Zerfallskonstante k ist der Begriff der Halbwertszeit tH .
Die Halbwertszeit gibt die Zeitspanne an, nach der sich die Aktivität jeweils
halbiert hat. Drücken Sie die Halbwertszeit tH in Abhängigkeit von der
Zerfallskonstanten k aus und berechnen Sie anschließend den Wert von tH für den
Kern des Kohlenstoffs C14 . (4 BE)