| 1.0 |
Gegeben ist die Funktion 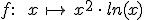 in der
größtmöglichen Definitionsmenge in der
größtmöglichen Definitionsmenge 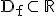 .
Ihr Graph wird mit .
Ihr Graph wird mit 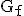 bezeichnet. bezeichnet. |
| |
| 1.1 | Geben Sie 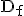 an und bestimmen Sie die Nullstelle
von f. (2 BE) an und bestimmen Sie die Nullstelle
von f. (2 BE) |
| |
| 1.2 | Ermitteln Sie das Monotonieverhalten von 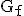 und daraus die Art und die Koordinaten seines Extrempunktes. und daraus die Art und die Koordinaten seines Extrempunktes.
(Zur Kontrolle: 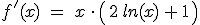 (6 BE) (6 BE) |
| |
1.3 | Bestimmen Sie das Verhalten von f(x) und der Ableitungsfunktion f '(x) für 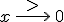 . (5 BE) . (5 BE) |
| |
| 1.4 | Untersuchen Sie, ob 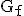 einen Wendepunkt besitzt. Begründen Sie Ihre Aussage nur unter
Verwendung der bisherigen Ergebnisse ohne Berechnung der 2. Ableitung
und geben Sie gegebenenfalls das Intervall an, in dem die Wendestelle
liegt. (4 BE)
einen Wendepunkt besitzt. Begründen Sie Ihre Aussage nur unter
Verwendung der bisherigen Ergebnisse ohne Berechnung der 2. Ableitung
und geben Sie gegebenenfalls das Intervall an, in dem die Wendestelle
liegt. (4 BE) |
| |
| 1.5 | Zeichnen Sie 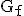 unter Berücksichtigung der bisherigen Ergebnisse für 0 < x ≤ 1,5 in ein kartesisches Koordinatensystem.
Beachten Sie dabei insbesondere das Verhalten von unter Berücksichtigung der bisherigen Ergebnisse für 0 < x ≤ 1,5 in ein kartesisches Koordinatensystem.
Beachten Sie dabei insbesondere das Verhalten von 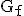 für für 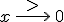 . (Maßstab: 1LE = 5cm) (4 BE) . (Maßstab: 1LE = 5cm) (4 BE) |
| |
| |
|
2.0 |
Gegeben ist die Funktion 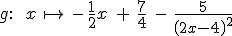 mit ihrer größtmöglichen Definitionsmenge
mit ihrer größtmöglichen Definitionsmenge 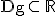 . Ihr Graph heißt . Ihr Graph heißt 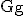 . . |
| |
|
2.1 |
Geben Sie 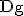 sowie die Lage und die Art der Definitionslücke von g an
und bestimmen Sie das Verhalten von g(x) bei Annäherung an
die Definitionslücke. Weisen Sie nach, dass
sowie die Lage und die Art der Definitionslücke von g an
und bestimmen Sie das Verhalten von g(x) bei Annäherung an
die Definitionslücke. Weisen Sie nach, dass 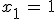 eine Nullstelle der Funktion g ist, und berechnen Sie die Koordinaten des Schnittpunktes eine Nullstelle der Funktion g ist, und berechnen Sie die Koordinaten des Schnittpunktes 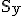 von von 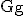 mit der y-Achse. mit der y-Achse.
(Hinweis: g hat als einzige Nullstelle 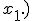 (6 BE) (6 BE) |
| |
|
2.2 |
Geben Sie die Gleichungen und die Art aller Asymptoten von 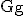 an und untersuchen Sie jeweils, ob sich der Graph an und untersuchen Sie jeweils, ob sich der Graph 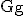 der schiefen Asymptote für der schiefen Asymptote für 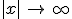 von oben oder von unten annähert. (4 BE) von oben oder von unten annähert. (4 BE) |
| |
|
2.3 |
Zeichnen Sie die Asymptoten in ein kartesisches Koordinatensystem und skizzieren Sie 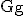 unter Berücksichtigung der bisherigen Erkenntnisse in die Zeichnung. (5 BE) unter Berücksichtigung der bisherigen Erkenntnisse in die Zeichnung. (5 BE) |
| |
|
2.4 |
Berechnen Sie das Integral 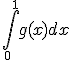 und erläutern Sie dessen geometrische Bedeutung. (5 BE) und erläutern Sie dessen geometrische Bedeutung. (5 BE) |
| |
| |
| |
|
3.0 |
In
einem Bach steigt nach einem Wolkenbruch die Wasserdurchflussmenge
deutlich an. An einer Messstelle wird die Wasserdurchflussmenge D(t)
(in 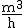 )
in Abhängigkeit von der Zeit t (in h) beobachtet.
Frühere Messungen ergaben, das für die Wasserdurchflussmenge für
t ≥ 0 annähernd die Beziehung )
in Abhängigkeit von der Zeit t (in h) beobachtet.
Frühere Messungen ergaben, das für die Wasserdurchflussmenge für
t ≥ 0 annähernd die Beziehung 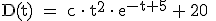 gilt, wobei c eine positive niederschlagsabhängige
Konstante ist. Im Funktionsterm und bei den Berechnungen wird auf die
Angabe von Einheiten verzichtet. Die Ergebnisse sind auf zwei
Nachkommastellen zu runden.
gilt, wobei c eine positive niederschlagsabhängige
Konstante ist. Im Funktionsterm und bei den Berechnungen wird auf die
Angabe von Einheiten verzichtet. Die Ergebnisse sind auf zwei
Nachkommastellen zu runden. |
| |
|
3.1 |
Nach 30 min beträgt die Durchflussmenge 25,6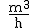 . Ermitteln Sie damit den Wert der Konstanten c. (Ergebnis: c ≈ 0,25) (3 BE) . Ermitteln Sie damit den Wert der Konstanten c. (Ergebnis: c ≈ 0,25) (3 BE) |
| |
|
3.2 |
Ermitteln Sie den Zeitpunkt 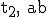 dem die Durchflussmenge wieder abnimmt. (5 BE) dem die Durchflussmenge wieder abnimmt. (5 BE) |
| |
|
3.3 |
Ab einer Durchflussmenge von 42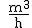 ufert der Bach aus. Stellen Sie fest, ob eine Ausuferung stattfindet. (2 BE) ufert der Bach aus. Stellen Sie fest, ob eine Ausuferung stattfindet. (2 BE) |
| |
|
3.4 |
Bestimmen Sie den Wert von D(t), der sich auf Grund der angegebenen Beziehung langfristig einstellt. (3 BE) |
| |
|
3.5 |
Gegeben ist die Funktion V mit 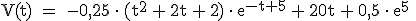 für t ≥ 0. Zeigen Sie, dass V eine Stammfunktion von D ist. für t ≥ 0. Zeigen Sie, dass V eine Stammfunktion von D ist.
Berechnen Sie das Integral 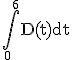 und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (6 BE) und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. (6 BE) |
| |
| |
 |
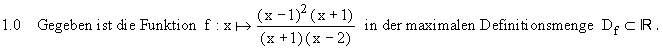 1.1 Geben Sie Df , die Lage und Vielfachheiten der Nullstellen sowie Art und Lage der Definitionslücken der Funktion f an
und untersuchen Sie das Verhalten von f(x) bei Annäherung an die Definitionslücken. ( 7 BE )
1.2.0 Im Folgenden betrachten wir die stetige Fortsetzung der Funktion f
1.1 Geben Sie Df , die Lage und Vielfachheiten der Nullstellen sowie Art und Lage der Definitionslücken der Funktion f an
und untersuchen Sie das Verhalten von f(x) bei Annäherung an die Definitionslücken. ( 7 BE )
1.2.0 Im Folgenden betrachten wir die stetige Fortsetzung der Funktion f
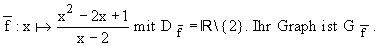 1.2.1 Bestimmen Sie die Gleichungen aller Asymptoten von
1.2.1 Bestimmen Sie die Gleichungen aller Asymptoten von 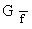 . ( 3 BE )
1.2.2 Ermitteln Sie die Art und die Koordinaten aller Extrempunkte von
. ( 3 BE )
1.2.2 Ermitteln Sie die Art und die Koordinaten aller Extrempunkte von 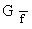 .
.
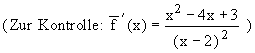 ( 7 BE )
1.2.3 Zeichnen Sie
( 7 BE )
1.2.3 Zeichnen Sie 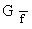 und seine Asymptoten mit Hilfe der bisherigen Ergebnisse und der Berechnung
weiterer geeigneter Funktionswerte im Intervall [ -2 ; 6 ] in ein Koordinatensystem. ( LE : 1 cm ) ( 5 BE )
1.2.4 Die Funktion F mit dem Graphen G F ist eine Stammfunktion der Funktion
und seine Asymptoten mit Hilfe der bisherigen Ergebnisse und der Berechnung
weiterer geeigneter Funktionswerte im Intervall [ -2 ; 6 ] in ein Koordinatensystem. ( LE : 1 cm ) ( 5 BE )
1.2.4 Die Funktion F mit dem Graphen G F ist eine Stammfunktion der Funktion 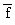 .
Geben Sie nur aufgrund bisheriger Ergebnisse das Monotonieverhalten von G F und die Abszissen seiner Wendepunkte
an. ( 5 BE )
1.2.5 Der Graph
.
Geben Sie nur aufgrund bisheriger Ergebnisse das Monotonieverhalten von G F und die Abszissen seiner Wendepunkte
an. ( 5 BE )
1.2.5 Der Graph 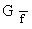 und die Geraden mit den Gleichungen y = x , x = 3 und x = b mit dem
rellen Parameter b > 3 begrenzen ein Flächenstück A.
Kennzeichnen Sie diese Fläche für b = 6 im Koordinatensystem von Aufgabe 1.2.3 und
berechnen Sie deren Flächenmaßzahl A( b) in Abhängigkeit von b. ( 5 BE )
1.2.6 Untersuchen Sie, ob
und die Geraden mit den Gleichungen y = x , x = 3 und x = b mit dem
rellen Parameter b > 3 begrenzen ein Flächenstück A.
Kennzeichnen Sie diese Fläche für b = 6 im Koordinatensystem von Aufgabe 1.2.3 und
berechnen Sie deren Flächenmaßzahl A( b) in Abhängigkeit von b. ( 5 BE )
1.2.6 Untersuchen Sie, ob 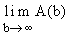 existiert. ( 2 BE )
2.0 Bei Patienten, die zur Nahrungsaufnahme nicht fähig sind, wird die künstliche Ernährung durch Infusion von Glucose in
die Blutbahn durchgeführt. U( t ) bezeichnet den Glucosegehalt im Blut eines Patienten ( in mg/dl ) zum Zeitpunkt t ( in
Stunden ) der Behandlung mit
existiert. ( 2 BE )
2.0 Bei Patienten, die zur Nahrungsaufnahme nicht fähig sind, wird die künstliche Ernährung durch Infusion von Glucose in
die Blutbahn durchgeführt. U( t ) bezeichnet den Glucosegehalt im Blut eines Patienten ( in mg/dl ) zum Zeitpunkt t ( in
Stunden ) der Behandlung mit 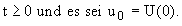 Dem Patieneten wird Glucose mit einer konstanten Rate pro
Stunde zugeführt. Der Abbau der Glucose erfolgt proportional zu dem vorhandenen Glucosegehalt mit der Konstanten
Dem Patieneten wird Glucose mit einer konstanten Rate pro
Stunde zugeführt. Der Abbau der Glucose erfolgt proportional zu dem vorhandenen Glucosegehalt mit der Konstanten
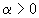 . Mit diesen Annahmen gilt ( ohne Berücksichtigung der Einheiten ) :
. Mit diesen Annahmen gilt ( ohne Berücksichtigung der Einheiten ) : 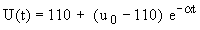 Bei der Rechnung kann auf Einheiten verzichtet werden. Die Ergebnisse sind auf zwei Nachkommastellen zu runden.
2.1 Bei einem Patienten, bei dem der Glucosegehalt im Blut am Anfang der Behandlung u 0 = 60 [ mg/dl ] beträgt,
wird nach 3 Stunden ein Glucosegehalt im Blut von U( 3 ) = 90 [ mg/dl ] festgestellt.
Bestimmen Sie für diesen Fall den Wert der Konstanten
Bei der Rechnung kann auf Einheiten verzichtet werden. Die Ergebnisse sind auf zwei Nachkommastellen zu runden.
2.1 Bei einem Patienten, bei dem der Glucosegehalt im Blut am Anfang der Behandlung u 0 = 60 [ mg/dl ] beträgt,
wird nach 3 Stunden ein Glucosegehalt im Blut von U( 3 ) = 90 [ mg/dl ] festgestellt.
Bestimmen Sie für diesen Fall den Wert der Konstanten 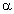 . ( 3 BE )
2.2 Setzen Sie nun
. ( 3 BE )
2.2 Setzen Sie nun 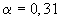 und berechnen Sie den Glucosegehalt im Blut des Patienten nach 5 Stunden. ( 2 BE )
2.3 Bestimmen Sie den Grenzwert der Funktion U für
und berechnen Sie den Glucosegehalt im Blut des Patienten nach 5 Stunden. ( 2 BE )
2.3 Bestimmen Sie den Grenzwert der Funktion U für 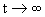 und interpretieren Sie diesen im Sinne der vorliegenden
Thematik. ( 3 BE )
3.0 Zur Versorgung der Raumstation ISS wird von Cap Canaveral eine Rakete gestartet.
Die Momentangeschwindigkeit der Rakete lässt sich, bis der gesamte Treibstoff verbrannt ist, näherungsweise mit der
Funktion
und interpretieren Sie diesen im Sinne der vorliegenden
Thematik. ( 3 BE )
3.0 Zur Versorgung der Raumstation ISS wird von Cap Canaveral eine Rakete gestartet.
Die Momentangeschwindigkeit der Rakete lässt sich, bis der gesamte Treibstoff verbrannt ist, näherungsweise mit der
Funktion 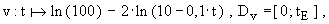 beschreiben.
Dabei ist t die Zeit, t E die Brenndauer jeweils in Sekunden und v( t ) die Geschwindigkeit in Kilometer pro Sekunde.
Bei den Berechnungen kann auf die Einheiten verzichtet werden,
die Ergebnisse sind gegebenenfalls auf zwei Nachkommastellen zu runden.
3.1 Berechnen Sie die Geschwindigkeit der Rakete zwei Sekunden nach dem Start
und den Zeitpunkt t 1 , zu dem die Geschwindigkeit
beschreiben.
Dabei ist t die Zeit, t E die Brenndauer jeweils in Sekunden und v( t ) die Geschwindigkeit in Kilometer pro Sekunde.
Bei den Berechnungen kann auf die Einheiten verzichtet werden,
die Ergebnisse sind gegebenenfalls auf zwei Nachkommastellen zu runden.
3.1 Berechnen Sie die Geschwindigkeit der Rakete zwei Sekunden nach dem Start
und den Zeitpunkt t 1 , zu dem die Geschwindigkeit 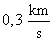 beträgt. ( 5 BE )
3.2 Nach dem Start wird die Masse m der Rakete ( in Tonnen ) durch die Verbrennung des Treibstoffs kleiner.
Es gilt :
beträgt. ( 5 BE )
3.2 Nach dem Start wird die Masse m der Rakete ( in Tonnen ) durch die Verbrennung des Treibstoffs kleiner.
Es gilt : 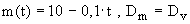 . Beim Start bestehen 85% der Gesamtmasse aus Treibstoff.
Berechnen Sie den Zeitpunkt t E , zu dem der gesamte Treibstoff verbrannt ist. ( 2 BE )
3.3 Bestimmen Sie das Monotonieverhalten von v und ermitteln Sie die maximale Geschwindigkeit der Rakete. ( 5 BE )
3.4 Zeigen Sie, dass
. Beim Start bestehen 85% der Gesamtmasse aus Treibstoff.
Berechnen Sie den Zeitpunkt t E , zu dem der gesamte Treibstoff verbrannt ist. ( 2 BE )
3.3 Bestimmen Sie das Monotonieverhalten von v und ermitteln Sie die maximale Geschwindigkeit der Rakete. ( 5 BE )
3.4 Zeigen Sie, dass 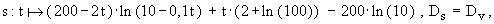 eine Stammfunktion von v ist,
berechnen Sie s ( t E ) - s ( 0 ) und interpretieren Sie diesen Wert im Sinne der Thematik. ( 6 BE )
eine Stammfunktion von v ist,
berechnen Sie s ( t E ) - s ( 0 ) und interpretieren Sie diesen Wert im Sinne der Thematik. ( 6 BE )

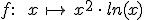 in der
größtmöglichen Definitionsmenge
in der
größtmöglichen Definitionsmenge 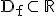 .
Ihr Graph wird mit
.
Ihr Graph wird mit 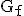 bezeichnet.
bezeichnet.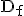 an und bestimmen Sie die Nullstelle
von f. (2 BE)
an und bestimmen Sie die Nullstelle
von f. (2 BE)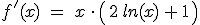 (6 BE)
(6 BE)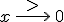 . (5 BE)
. (5 BE)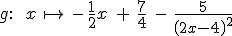 mit ihrer größtmöglichen Definitionsmenge
mit ihrer größtmöglichen Definitionsmenge 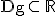 . Ihr Graph heißt
. Ihr Graph heißt 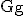 .
.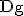 sowie die Lage und die Art der Definitionslücke von g an
und bestimmen Sie das Verhalten von g(x) bei Annäherung an
die Definitionslücke. Weisen Sie nach, dass
sowie die Lage und die Art der Definitionslücke von g an
und bestimmen Sie das Verhalten von g(x) bei Annäherung an
die Definitionslücke. Weisen Sie nach, dass 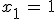 eine Nullstelle der Funktion g ist, und berechnen Sie die Koordinaten des Schnittpunktes
eine Nullstelle der Funktion g ist, und berechnen Sie die Koordinaten des Schnittpunktes 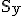 von
von 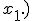 (6 BE)
(6 BE)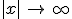 von oben oder von unten annähert. (4 BE)
von oben oder von unten annähert. (4 BE)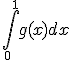 und erläutern Sie dessen geometrische Bedeutung. (5 BE)
und erläutern Sie dessen geometrische Bedeutung. (5 BE)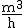 )
in Abhängigkeit von der Zeit t (in h) beobachtet.
Frühere Messungen ergaben, das für die Wasserdurchflussmenge für
t ≥ 0 annähernd die Beziehung
)
in Abhängigkeit von der Zeit t (in h) beobachtet.
Frühere Messungen ergaben, das für die Wasserdurchflussmenge für
t ≥ 0 annähernd die Beziehung 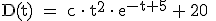 gilt, wobei c eine positive niederschlagsabhängige
Konstante ist. Im Funktionsterm und bei den Berechnungen wird auf die
Angabe von Einheiten verzichtet. Die Ergebnisse sind auf zwei
Nachkommastellen zu runden.
gilt, wobei c eine positive niederschlagsabhängige
Konstante ist. Im Funktionsterm und bei den Berechnungen wird auf die
Angabe von Einheiten verzichtet. Die Ergebnisse sind auf zwei
Nachkommastellen zu runden.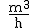 . Ermitteln Sie damit den Wert der Konstanten c. (Ergebnis: c ≈ 0,25) (3 BE)
. Ermitteln Sie damit den Wert der Konstanten c. (Ergebnis: c ≈ 0,25) (3 BE)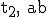 dem die Durchflussmenge wieder abnimmt. (5 BE)
dem die Durchflussmenge wieder abnimmt. (5 BE)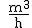 ufert der Bach aus. Stellen Sie fest, ob eine Ausuferung stattfindet. (2 BE)
ufert der Bach aus. Stellen Sie fest, ob eine Ausuferung stattfindet. (2 BE)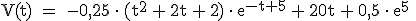 für t ≥ 0. Zeigen Sie, dass V eine Stammfunktion von D ist.
für t ≥ 0. Zeigen Sie, dass V eine Stammfunktion von D ist.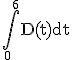 und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik.
und interpretieren Sie das Ergebnis im Sinne der vorliegenden Thematik. 