1.0     

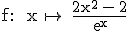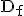Gegeben ist die Funktion   mit = IR. Ihr Graph sei   .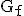

Geben Sie die Schnittpunkte von 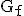   mit den Koordinatenachsen an.     (3 BE)

Untersuchen Sie das Verhalten von f(x) für  x 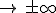  und geben Sie die Gleichung der Asymptote von  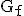  an.     (4 BE)

Bestimmen Sie die Art und die Koordinaten der Extrempunkte von 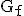 .  Runden Sie die Ordinaten auf zwei Nachkommastellen.
( Teilergebnis: 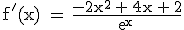 )     (9 BE)

Zeichnen Sie 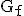   unter Verwendung der bisherigen Ergebnisse und der Berechnung weiterer geeigneter Funktionswerte im Intervall  [–1,2 ; 6]  in ein kartesisches Koordinatensystem.     (5 BE)

1.5

Zeigen Sie, dass die Funktion 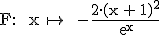   mit 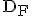= IR eine Stammfunktion von  f  ist und berechnen Sie die exakte Flächenmaßzahl des Flächenstücks, das von 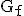und der x-Achse unterhalb der x-Achse eingeschlossen wird.     (5 BE)

1.6.0

Gegeben ist die Funktion 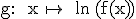   mit maximaler Definitionsmenge 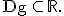Ihr Graph ist 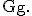Lösen Sie die folgenden Aufgaben möglichst unter Verwendung der Eigenschaften von  f  (Aufgaben 1.1 – 1.4).

Geben Sie 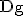an und begründen Sie, dass g nur genau eine Nullstelle hat.     (4 BE)

Bestimmen Sie das Verhalten von g an den Rändern von 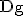.     (4 BE)

Untersuchen Sie 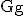auf Extrempunkte und geben Sie gegebenenfalls deren Koordinaten und Art an.     (5 BE)

2.0

Zur Unterstützung der Stromversorgung einer Gemeinde wird in der Zeit von 12:00 Uhr bis 18:00 Uhr ein kleines Wasserkraftwerk zugeschaltet. Durch unterschiedlichen Wasserdurchfluss in 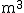pro Minute (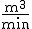) kann die Stromabgabe an den Energiebedarf der Gemeinde angepasst werden. Der Wasserdurchfluss an einem bestimmten Tag wird in Abhängigkeit von der Tageszeit annähernd durch den Funktionsterm 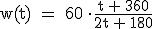beschrieben. Dabei bedeutet t die Zeit in Minuten (min) von 12:00 Uhr bis 18:00 Uhr, das heißt 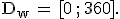Auf die Mitführung von Einheiten kann verzichtet werden.

2.1

Berechnen Sie den Wasserdurchfluss um 13:00 Uhr und um 15:00 Uhr.     (2 BE)

2.2

Ermitteln Sie, um welche Uhrzeit im betrachteten Zeitraum der Wasserdurchfluss und damit die Stromerzeugung des Elektrizitätswerkes am größten ist.     (4 BE)

2.3.0

Das Integral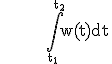  gibt die in der Zeit von  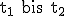  durchgeflossene Wassermenge an.

2.3.1

Zeigen Sie, dass sich der Funktionsterm von w auch in der Form 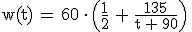schreiben lässt, und berechnen Sie W(t) = ∫w(t)dt.     (4 BE)

2.3.2

Zeichnen Sie den Graphen der Funktion w in ein geeignetes Koordinatensystem.
(Maßstab: t-Achse: 1cm 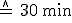; w-Achse: 1cm )     (5 BE)

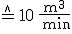2.3.3

Entnehmen Sie aus der Zeichnung von 2.3.2 die Uhrzeit, zu der etwa die Hälfte der Wassermenge durchgeströmt ist, die von 12:00 Uhr bis 18:00 Uhr durchgeflossen ist. Überprüfen Sie Ihre Annahme durch Rechnung und kommentieren Sie das Ergebnis.     (6 BE)