Prüfung zur Erlangung der fachgebundenen Hochschulreife
Frühjahr 1999
Aufgabengruppe A: A I A II
A I
1.
Gegeben ist die Funktion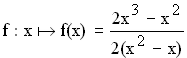 
mit maximaler Definitionsmenge D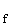
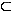IR.
1.1
Bestimmen Sie Df , die Nullstelle von f, und untersuchen Sie das Verhalten von f(x) bei Annäherung an die Definitionslücken. Geben Sie auch die Art der Definitionslücken an. (7 BE)
1.2
Zeigen
Sie, dass sich der Funktionsterm f(x) darstellen lässt in der Form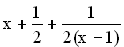 
,
1.3
Bestimmen Sie ohne Verwendung der 2.Ableitung die Art und die Koordinaten der Extrempunkte des Graphen von f auf zwei Dezimalstellen genau. (8 BE)
1.4
Zeichnen Sie die Asymptoten und den Graphen von f für | x | ≤ 3 unter Verwendung der bisherigen Ergebnisse sowie der Werte f(-3) und f(3) in ein kartesisches Koordinatensystem (1LE = 2cm). (5 BE)
1.5
Bestimmen
Sie die reelle Zahl c so, dass für 0 < x < 1 die Funktion F mit
(Zur Kontrolle: c = 0,5)
2.
Nun ist die Funktion g: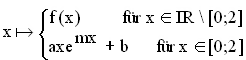 
mit a, b, m 
IR und f aus Aufgabe 1 gegeben.
2.1
Ermitteln Sie die Koeffizienten a, b und m so, dass g an der Stelle x = 0 stetig und differenzierbar und zusätzlich an der Stelle x = 2 stetig ist. (8 BE)
(Zur Kontrolle: a =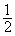 
; b = 0; m = 
)
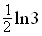2.2
Zeigen Sie, dass g aus Aufgabe 2.1 an der Stelle x = 2 nicht differenzierbar ist und dass der Graph von g im Intervall ]0; 2[ linksgekrümmt ist. Zeichnen Sie den Graphen von g unter Verwendung bisheriger Ergebnisse in das Koordinatensystem von Aufgabe 1.4 ein. (7 BE)
3.
Der Durchmesser d (in Metern) einer Durchschnittsfichte gemessen in Brusthöhe in Abhängigkeit vom Alter t des Baumes (in Jahren) lässt sich näherungsweise durch den Funktionsterm
d(t) =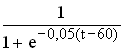 
darstellen.
3.1
Ermitteln Sie den Durchmesser einer Durchschnittsfichte im Alter von 50 bzw. 100 Jahren. (2 BE)
3.2
Untersuchen Sie das Verhalten der Funktionswerte d(t) für t
0 sowie für sehr große t-Werte und erläutern Sie damit Grenzen des verwendeten Wachstumsmodells. (4 BE)
3.3
Mit einem Maßband wird als Umfang einer Fichte 1,80 Meter gemessen. Berechnen Sie das Alter dieser Fichte (4 BE)
A II
1.
Gegeben ist die Funktion g: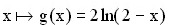 
mit maximaler Definitionsmenge D
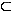IR .
1.1
Bestimmen Sie Dg und die Nullstelle von g, und untersuchen Sie das Verhalten von g(x) an den Rändern der Definitionsmenge. (4 BE)
1.2
Untersuchen Sie das Monotonieverhalten von g und zeigen Sie, dass g weder Extrem- noch Wendestellen besitzt. (5 BE)
1.3
Zeichnen Sie den Graphen von g für –6 < x < 2 anhand geeigneter Funktionswerte in ein kartesisches Koordinatensystem (1LE =1 cm). (3 BE)
1.4
Ermitteln Sie die Werte der reellen Parameter a, b und c so, dass die Funktion S mit der Gleichung
(Zur Kontrolle: a = 2; b = –4; c = –2)
2.
Nun ist die Funktion f: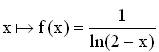 
mit der maximalen Definitionsmenge D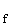 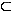] –∞; 2 [ gegeben.
2.1
Bestimmen Sie Df und untersuchen Sie das Verhalten von f(x) an den Rändern der Definitionsmenge und an der Definitionslücke. (5 BE)
2.2
Bestimmen Sie die maximalen Monotonieintervalle des Graphen von f. Begründen Sie, dass f nicht in der gesamten Definitionsmenge streng monoton ist. (5 BE)
(Zur Kontrolle: f '(x) =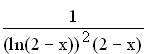 
)
2.3
Zeigen Sie, dass der Graph von f einen Wendepunkt besitzt und berechnen Sie dessen Koordinaten. (6 BE)
2.4
Berechnen Sie die Abszissen der Schnittpunkte der Graphen von f und g. (4 BE)
2.5
Verwenden Sie die bisherigen Ergebnisse und zeichnen Sie den Graphen von f in das Koordinatensystem von Aufgabe 1.3 ein. (3 BE)
3.
Die Wirtschaftlichkeit W einer Produktion wird gemessen durch den Quotienten aus dem erzielten Ertrag E (Wert der produzierten Leistung) und dem Aufwand A (Wert der eingesetzten Produktionsfaktoren). In Abhängigkeit von der Produktionsmenge x ≥ 0 gilt für die Ertragsfunktion
3.1
Erläutern Sie, welche Bedeutung die Ungleichung W(x) > 1 für diese Produktion hat, und bestimmen Sie die Lösungsmenge dieser Ungleichung. (5 BE)
3.2
Zeigen Sie, dass die Wirtschaftlichkeit W ein Maximum besitzt und berechnen Sie dieses.
(Zur Kontrolle: xmax ≈ 707) (5 BE)
3.3
Stellen Sie fest, ob bei der in Aufgabe 3.2 ermittelten Produktionsmenge auch der größtmögliche Gewinn erzielt wird und erläutern Sie den Sachverhalt. (5 BE)