1.0
Gegeben ist das lineare Gleichungssystem A![]() mit A =
mit A = 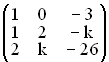 und
und 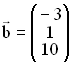 sowie
sowie  IR.
IR.
Untersuchen Sie durch eine Rangbetrachtung, für welche k  IR das Gleichungssystem keine, genau eine oder unendlich viele Lösungen besitzt, und geben Sie für k = 8 die Lösungsmenge an. (10 BE)
IR das Gleichungssystem keine, genau eine oder unendlich viele Lösungen besitzt, und geben Sie für k = 8 die Lösungsmenge an. (10 BE)
Interpretieren Sie die Spalten der Matrix A als Vektoren des IR3. Welche Aussage ergibt sich aus Aufgabe 1.1 über die lineare Unabhängigkeit dieser Vektoren ? (3 BE)
Nun wird die Matrix B = ![]() betrachtet.
betrachtet.
Ermitteln Sie die Menge aller (2,2)-Matrizen D, für die gilt: B · D = D · B. Geben Sie sodann ein Beispiel für eine Matrix C an, für die die Matrizenmultiplikation B · C nicht kommutativ ist. (7 BE)
2.2
Bestimmen Sie die reellen Zahlen α und β, für die gilt: B3 = α·B + β·B2. Hierbei ist
2.3
Nun sei n eine beliebige natürliche Zahl. Folgern Sie aus dem Vergleich von B2 und B3 eine Beziehung für die Matrix Bn. Überprüfen Sie Ihre Vermutung durch Berechnen von
In einem kartesischen Koordinatensystem des IR3 sind die Punkte
3.1
Begründen Sie, welche besondere Lage die Gerade QR im Koordinatensystem besitzt, und berechnen Sie die Koordinaten des Schnittpunktes von QR mit der ![]() -Ebene. (4 BE)
-Ebene. (4 BE)
3.2
Untersuchen Sie, ob es eine Ebene  E gibt, die die Gerade QR und die Gerade mit der Gleichung
E gibt, die die Gerade QR und die Gerade mit der Gleichung 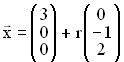 mit
mit  IR
IR
Ein Objekt bewegt sich ohne Richtungswechsel mit konstanter Geschwindigkeit auf der Geraden QR. Es startet in Q und erreicht 10 Sekunden später R. Berechnen Sie, in welchem Punkt es sich 45 Sekunden nach dem Start befindet. (3 BE)

In einem kartesischen Koordinatensystem sind der Punkt
einem kartesischen Koordinatensystem sind der Punkt  (3 –
m | m –
1 | m –
2)
(3 –
m | m –
1 | m –
2)  IR
IR 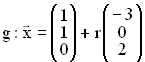 mit r
mit r  IR gegeben.
IR gegeben.
1.1
Untersuchen Sie, für welche m  IR durch die Gerade g und den Punkt Am eine Ebene E festgelegt
IR durch die Gerade g und den Punkt Am eine Ebene E festgelegt
1.2
Stellen Sie für m = 3 je eine Gleichung der Ebene E in Parameterform und parameterfreier Darstellung
(Mögliches Ergebnis: 2x1 – x2 + 3x3 – 1 = 0)
1.3
Nun sind die Punkte P(3 | 4 | –
2) und Qa(1 –
2a | a –
2 | a + 2) mit  IR
IR
2.0
Gegeben sind die Matrix 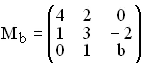 und der Vektor
und der Vektor 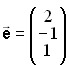 mit
mit  IR.
IR.
2.1
Bestimmen Sie k und b so, dass die Gleichung 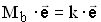 mit k
mit k  IR erfüllt ist. (4 BE)
IR erfüllt ist. (4 BE)
2.2
Untersuchen Sie anhand einer Rangbetrachtung, für welche Zahlen b das Gleichungssystem 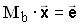 genau eine bzw. keine Lösung besitzt.
genau eine bzw. keine Lösung besitzt.
3.0
Die drei Abteilungen F, G und H eines Unternehmens sind nach dem Leontief-Modell miteinander verbunden (Angaben in Mengeneinheiten ME):
|
F |
G |
H |
Markt |
|
|
F |
20 |
3 |
2 |
15 |
|
G |
8 |
9 |
6 |
7 |
|
H |
4 |
3 |
0 |
3 |
Bestimmen Sie die Inputmatrix A. (3 BE)
3.2
Es wird eine Produktionserhöhung in Abteilung F um 20 und in Abteilung G um 30 Einheiten bei gleichbleibender Produktion in H vorgeschlagen. Beurteilen Sie anhand des neuen Marktvektors, ob dies möglich ist. (3 BE)
3.3
Berechnen Sie zum Marktvektor 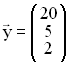 den Produktionsvektor. (4 BE)
den Produktionsvektor. (4 BE)
Nun soll Abteilung F die Produktion auf 60 ME erhöhen und die Abteilungen F und G sollen jeweils mindestens 20 ME an den Markt abgeben. Stellen Sie die drei sich ergebenden Bedingungen in einem 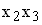 -Koordinatensystem
-Koordinatensystem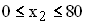 )
)
