1.0 | Im IR sind die Ebenen E sind die Ebenen E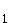 : –3x : –3x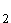 + x + x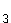 = 0, E = 0, E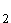 : : 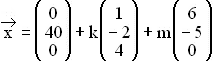 mit k, m mit k, m  IR, E IR, E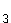 : 4x : 4x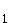 + x + x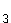 = 96 und E = 96 und E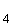 : –4x : –4x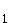 + x + x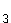 = 0 gegeben. = 0 gegeben. |
| |
| 1.1 | Wandeln Sie die Gleichung von E2 in Koordinatenform um.
(Mögliches Ergebnis für E2: 20x1 + 24x2 + 7x3 – 960 = 0) (4 BE) |
| |
| 1.2 | Weisen Sie nach, dass die vier Ebenen E1, E2, E3 und E4 genau einen Punkt S gemeinsam haben, und berechnen Sie dessen Koordinaten. (5 BE) |
| |
| 1.3 | Zeigen Sie, dass die Ebene E1 die x1-Achse enthält. (2 BE) |
| |
1.4 | Die Ebene E3 schneidet die x1-Achse im Punkt A und E2 schneidet die x2-Achse im Punkt C. Die Schnittgerade der Ebenen E2 und E3 trifft die x1x2-Ebene im Punkt B. Bestimmen Sie die Koordinaten der Punkte A, B und C. (7 BE) |
| |
| |
2.0 | Für eine Kunstausstellung soll ein futuristischer pyramidenförmiger Pavillon mit dem Viereck ABCO als Grundfläche und dem Punkt S als Pyramidenspitze errichtet werden (siehe Skizze). | 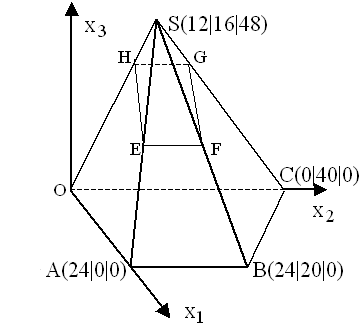 |
| |
2.1 | Begründen Sie: Das Viereck OABC ist ein Trapez. (2 BE) |
| |
2.2 | Die Mittelpunkte E und F der Kanten [AS] und [BS] sollen zusammen mit den Punkten G und H die Eckpunkte eines Parallelogramms EFGH darstellen, das als eine schräg liegende Ausstellungsplattform dienen soll. Dabei soll der Punkt G auf der Kante [CS] und der Punkt H auf der Kante [OS] liegen. Berechnen Sie die Koordinaten der Punkte E, F, G und H.
(Teilergebnisse: E(18|8|24); F(18|18|24); G(9|22|36) ) (10 BE) |
| |
2.3 | Überprüfen Sie rechnerisch, ob die Vektoren 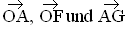 linear unabhängig sind. Schließen Sie aus dem Ergebnis Ihrer Untersuchung auf die gegenseitige Lage der Geraden OF und AG. (5 BE) linear unabhängig sind. Schließen Sie aus dem Ergebnis Ihrer Untersuchung auf die gegenseitige Lage der Geraden OF und AG. (5 BE) |
| |
| |
3. | Mit M wird die Menge aller Matrizen der Form A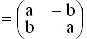 mit a, b mit a, b  IR bezeichnet, die bezüglich der üblichen Verknüpfungen „+“ und „·“ ein reeller Vektorraum ist. Geben Sie eine geeignete Basis des Vektorraums an und begründen Sie, welche Dimension dieser Vektorraum hat. (5 BE) IR bezeichnet, die bezüglich der üblichen Verknüpfungen „+“ und „·“ ein reeller Vektorraum ist. Geben Sie eine geeignete Basis des Vektorraums an und begründen Sie, welche Dimension dieser Vektorraum hat. (5 BE) |
| |

|
1.0 | Im IR sind die Geraden g: sind die Geraden g: 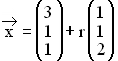 und h: und h: 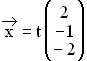 mit r, t mit r, t  IR sowie der Punkt Q (0 | 0 | –1) gegeben.
IR sowie der Punkt Q (0 | 0 | –1) gegeben. |
| |
1.1 | Bestimmen Sie eine Gleichung derjenigen Ebene E in parameterfreier Darstellung, die den Punkt Q und die Gerade g enthält. (5 BE)
(Mögliches Ergebnis für E: 2x2 – x3 – 1 = 0) |
| |
1.2 | Untersuchen Sie, welche Lage die Gerade h zur Ebene E und zur Geraden g hat. (6 BE) |
| |
1.3 | Beschreiben Sie die besondere Lage der Ebene E im Koordinatensystem, und ermitteln Sie eine Gleichung der Schnittgeraden zwischen der Ebene E und der x1x3-Ebene. (5 BE) |
| |
| |
2. | Im Vektorraum der Polynome vom Grad höchstens 2 sind die Vektoren p1 = 3x2 – x + 2, p2 = –x2 + 1 und p3 = 3x + 2 gegeben. Zeigen Sie, dass die drei Vektoren linear unabhängig sind, begründen Sie sodann, dass diese drei Vektoren eine Basis des Vektorraumes bilden, und berechnen Sie die Koordinaten des Vektors p4 = 5x2 + 12x + 20 bezüglich dieser Basis. (6 BE) |
| |
| |
3.0 |
Die drei Werke A, B und C eines Unternehmens sind nach dem Leontief-Modell verflochten. (Produktionszahlen pro Jahr in ME) | 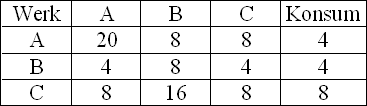 |
|
3.1 | Bestimmen Sie die Inputmatrix. (3 BE) |
| |
3.2 | Im nächsten Jahr sollen sich die Lieferungen an die Kunden bei gleich bleibender Inputmatrix wie folgt ändern: Von Werk A und C gehen die Lieferungen um jeweils 25 % zurück, von Werk B verdoppeln sie sich. Bestimmen Sie den Produktionsvektor 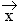 . (6 BE) . (6 BE) |
| |
3.3 | Für die längerfristige Planung ist bei gleichbleibender Inputmatrix folgender Produktionsvektor mit t die längerfristige Planung ist bei gleichbleibender Inputmatrix folgender Produktionsvektor mit t  [ 0 ; ∞ [ vorgesehen: [ 0 ; ∞ [ vorgesehen: 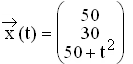 . Bestimmen Sie diejenigen t-Werte, für die sich bei allen 3 Werken für die Marktabgabe mögliche Werte ergeben und die Lieferung von Werk C an die Kunden größer ist als die von Werk B. Ermitteln Sie außerdem denjenigen t-Wert, für den die Summe der Marktabgaben aller 3 Werke innerhalb des möglichen Bereichs maximal wird und bestimmen Sie diesen Maximalwert. (9 BE) . Bestimmen Sie diejenigen t-Werte, für die sich bei allen 3 Werken für die Marktabgabe mögliche Werte ergeben und die Lieferung von Werk C an die Kunden größer ist als die von Werk B. Ermitteln Sie außerdem denjenigen t-Wert, für den die Summe der Marktabgaben aller 3 Werke innerhalb des möglichen Bereichs maximal wird und bestimmen Sie diesen Maximalwert. (9 BE)

|
 sind die Ebenen E
sind die Ebenen E : –3x
: –3x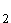 + x
+ x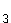 = 0, E
= 0, E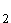 :
: 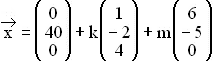 mit k, m
mit k, m  IR,
IR, 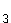 : 4x
: 4x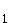 + x
+ x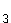 = 96
= 96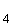 : –4x
: –4x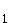 + x
+ x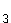 = 0
= 0 
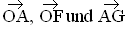 linear unabhängig sind. Schließen Sie aus dem Ergebnis Ihrer Untersuchung auf die gegenseitige Lage der Geraden OF und AG. (5 BE)
linear unabhängig sind. Schließen Sie aus dem Ergebnis Ihrer Untersuchung auf die gegenseitige Lage der Geraden OF und AG. (5 BE)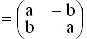 mit a, b
mit a, b  IR bezeichnet, die bezüglich der üblichen Verknüpfungen „+“ und „·“ ein reeller Vektorraum ist. Geben Sie eine geeignete Basis des Vektorraums an und begründen Sie, welche Dimension dieser Vektorraum hat. (5 BE)
IR bezeichnet, die bezüglich der üblichen Verknüpfungen „+“ und „·“ ein reeller Vektorraum ist. Geben Sie eine geeignete Basis des Vektorraums an und begründen Sie, welche Dimension dieser Vektorraum hat. (5 BE)
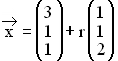 und h:
und h: 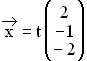 mit
mit 
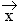 . (6 BE)
. (6 BE) die längerfristige Planung ist bei gleichbleibender Inputmatrix folgender Produktionsvektor mit t
die längerfristige Planung ist bei gleichbleibender Inputmatrix folgender Produktionsvektor mit t 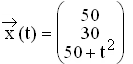 . Bestimmen Sie diejenigen t-Werte, für die sich bei allen 3 Werken für die Marktabgabe mögliche Werte ergeben und die Lieferung von Werk C an die Kunden größer ist als die von Werk B. Ermitteln Sie außerdem denjenigen
. Bestimmen Sie diejenigen t-Werte, für die sich bei allen 3 Werken für die Marktabgabe mögliche Werte ergeben und die Lieferung von Werk C an die Kunden größer ist als die von Werk B. Ermitteln Sie außerdem denjenigen