1.0
Gegeben sind im IR die Vektoren
die Vektoren 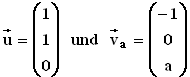 mit a
mit a  IR sowie die Punkte P(0 | 4 | 1) und Q(5 | 6 | 7).
IR sowie die Punkte P(0 | 4 | 1) und Q(5 | 6 | 7).
1.1
Berechnen Sie den Wert von a, für den die Geraden 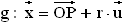 und
und 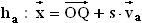 mit
mit  IR
IR
(Mögliche Lösung: E: 2x1 – 2x2 – x3 + 9 = 0 ) (7 BE)
1.2
Ermitteln Sie eine Gleichung der Schnittgeraden k der Ebene E und der x2x3-Koordinatenebene. (4 BE)
1.3
Der Punkt R (r1 | r2 | 4) mit r1, r2  IR liegt auf der Geraden PQ. Ermitteln Sie die Werte r1 und r2 sowie das Teilverhältnis λ von R bezüglich der Strecke [PQ]. (4 BE)
IR liegt auf der Geraden PQ. Ermitteln Sie die Werte r1 und r2 sowie das Teilverhältnis λ von R bezüglich der Strecke [PQ]. (4 BE)
2.0
Die drei Zweigwerke U, V, W eines Betriebes sind nach dem Leontief-Modell untereinander und mit dem Markt verflochten. Die derzeitige Produktion beträgt im Werk U 800 ME, im Werk V 450 ME und im Werk W 300 ME. Die Verflechtung ist der nebenstehenden Tabelle zu entnehmen.
|
U |
V |
W |
Markt |
|
|
U |
a |
450 |
180 |
10 |
|
V |
0 |
b |
0 |
360 |
|
W |
160 |
0 |
c |
80 |
2.1
Ermitteln Sie die Werte a, b und c und die Inputmatrix A.
2.2
Die Abgabe von U an den Markt soll sich auf 62 ME erhöhen, ohne dass sich die Abgaben von V und W an den Markt ändern. Ermitteln Sie die dazu benötigten Produktionsmengen der einzelnen Zweigwerke. (5 BE)
2.3
Nun wird festgestellt, dass die Produktionsmengen in V und W doch nicht erhöht werden können, sondern lediglich die Produktion in U ausgeweitet werden kann. Es wird für jede produzierte und an den Markt abgegebene Mengeneinheit 1 GE (Geldeinheit) erzielt. Ermitteln Sie die maximal mögliche Gesamteinnahme, die durch die Ausweitung der Produktion in U erreicht werden kann. (6 BE)
3.0
Gegeben sind die Matrizen
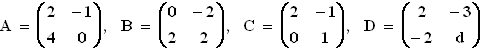 und
und 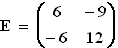 mit d
mit d  IR.
IR.
3.1
Bestimmen Sie den Wert von d, für den die Matrix D als Linearkombination von A, B und C dargestellt werden kann.
(Ergebnis: d = 4 ) (6 BE)
3.2
Untersuchen Sie unter Verwendung von Aufgabe 3.1, ob die Matrizen A, B, C und E linear abhängig sind. (4 BE)

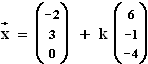 und h
und h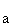 :
: 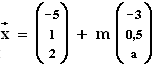 mit k, m, a
mit k, m, a 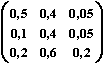 und der Marktvektor
und der Marktvektor 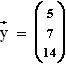 .
. und erstellen Sie die Input-Output-Tabelle.
und erstellen Sie die Input-Output-Tabelle. , in dem die Produktionsmenge von W variieren kann. Bestimmen Sie den Marktvektor
, in dem die Produktionsmenge von W variieren kann. Bestimmen Sie den Marktvektor 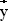 , falls die Produktionsmenge von W auf den kleinsten Wert absinkt.
, falls die Produktionsmenge von W auf den kleinsten Wert absinkt. (6 BE)
(6 BE)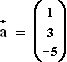 ,
, 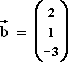 ,
, 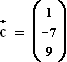 und
und 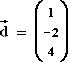 gegeben.
gegeben. als Linearkombination von
als Linearkombination von 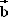 ,
, 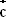 und
und 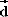 darstellen lässt, aber
darstellen lässt, aber  (8 BE)
(8 BE)