1.0
Die Verflechtungen dreier Abteilungen U, V und W eines Betriebes untereinander und mit dem Markt nach dem Leontief-Modell sind durch die Inputmatrix 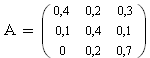 gegeben.
gegeben.
1.1
Berechnen Sie die Produktionsmengen in den einzelnen Abteilungen, wenn mit dem Marktabgabevektor 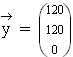 gerechnet wird. (6 BE)
gerechnet wird. (6 BE)
1.2
Geben Sie für die Produktion nach Teilaufgabe 1.1 die Verflechtungstabelle mit allen intern verbrauchten und an den Markt gelieferten Mengen an. (3 BE)
1.3
Für eine kurzfristige Planung gilt der Produktionsvektor 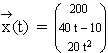 mit
mit 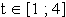 . Mit s(t) wird die Summe der an den Markt abgegebenen Mengen in Abhängigkeit von t bezeichnet. Bestimmen Sie den Wert von t, für den
. Mit s(t) wird die Summe der an den Markt abgegebenen Mengen in Abhängigkeit von t bezeichnet. Bestimmen Sie den Wert von t, für den
2.0
Im 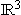 sind die Punke A(–1 | 1 | 1), B
sind die Punke A(–1 | 1 | 1), B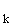 (1 | –k | –1), C
(1 | –k | –1), C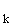 (2 | 2 – k | –8) mit k
(2 | 2 – k | –8) mit k 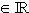 gegeben.
gegeben.
2.1
Berechnen Sie die Werte von k, für welche die Vektoren 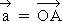 ,
, 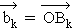 und
und 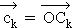 eine Basis des rellen Vektorraums
eine Basis des rellen Vektorraums 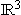 bilden. (6 BE)
bilden. (6 BE)
2.2
Untersuchen Sie die gegenseitige Lage der Vektoren 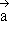 ,
, 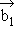 und
und 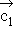 (also k = 1) und stellen Sie eine mögliche gegenseitige Lage in einer Skizze dar. (3 BE)
(also k = 1) und stellen Sie eine mögliche gegenseitige Lage in einer Skizze dar. (3 BE)
2.3
Bestimmen Sie für die Ebene E: 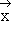 =
= 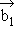 + r ·
+ r · 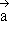 + s ·
+ s · 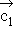 mit r, s
mit r, s 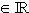 eine parameterfreie Gleichung. Welche besondere Lage hat E im Koordinatensystem? (6 BE)
eine parameterfreie Gleichung. Welche besondere Lage hat E im Koordinatensystem? (6 BE)
(mögliches Ergebnis:  E: 3x1 + 2x2 + x3 = 0)
E: 3x1 + 2x2 + x3 = 0)
2.4
Untersuchen Sie die gegenseitige Lage der Geraden 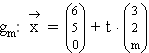 mit t, m
mit t, m 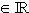 und der Ebene E in Abhängigkeit von m. Berechnen Sie für m = 1 die Koordinaten des Schnittpunktes S von E und g1. (5 BE)
und der Ebene E in Abhängigkeit von m. Berechnen Sie für m = 1 die Koordinaten des Schnittpunktes S von E und g1. (5 BE)
2.5
Der Punkt Q teilt die Strecke [PS] mit P(6 | 5 | 0) und S(0 | 1 | –2) im Verhältnis λ = –2. Geben Sie anhand einer Skizze die Lage des Punktes S bezüglich der Strecke [PQ] an und berechnen Sie die Koordinaten von Q. (4 BE)

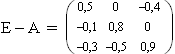
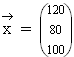 ist. (4 BE)
ist. (4 BE)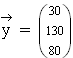 . Berechnen Sie den zugehörigen Produktionsvektor. (5 BE)
. Berechnen Sie den zugehörigen Produktionsvektor. (5 BE)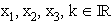 ) :
) :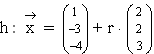 mit r
mit r 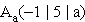 und
und 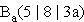 mit
mit