1       

Ermitteln Sie die Werte von k, für welche die drei Vektoren 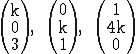   mit  k   eine Basis des 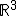   bilden.   (5 BE)

2.0

In einem Koordinatensystem des 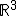   ist die Ebene  E  durch die Punkte  A(–7 | 5 | –1),  B(–3 | 10 | –4)  und  C(–7 | 15 | –1)  festgelegt.

2.1

Ermitteln Sie eine Gleichung der Ebene  E  in parameterfreier Form und beschreiben Sie die besondere Lage der Ebene  E  im Koordinatensystem.
(mögliches Ergebnis: E: 3x₁ + 4x₃ + 25 = 0)   (5 BE)

2.2

Der Punkt  M  ist der Mittelpunkt der Strecke  [AB]  und die Gerade  g  ist durch die Punkte  M  und  C  bestimmt. Ermitteln Sie eine Gleichung von  g.
(mögliches Ergebnis: 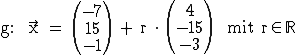)   (3 BE)

2.3

Bestimmen Sie die Koordinaten des Schnittpunktes  S  der Geraden  g  mit der  x₁x₃-Ebene  und ermitteln Sie, in welchem Verhältnis  S  die Strecke  [MC]  teilt. Stellen Sie in einer Skizze die gegenseitige Lage der Punkte  A,  B,  C,  M  und  S  in der Ebene  E  dar.
(Teilergebnis: S(–3 | 0 | –4) )   (6 BE)

2.4

Nun sind die Geraden 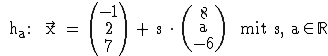gegeben. Zeigen Sie, dass alle Geraden  h 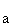echt parallel zur Ebene  E  verlaufen, und bestimmen Sie die gegenseitige Lage von  g (Aufgabe 2.2) und  h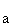 in Abhängigkeit von  a.   (6 BE)

3.0

Die drei Zweigwerke P, Q und R eines Unternehmens sind untereinander und mit dem Markt nach dem Leontief- Modell verflochten. Das nebenstehende Diagramm stellt die Verflechtung dar.

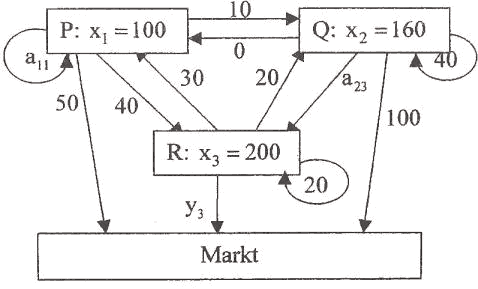
3.1

Bestimmen Sie die Inputmatrix  A.   (4 BE)

3.2

In einem früheren Zeitraum war der Marktvektor 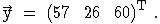   Berechnen Sie den zugehörigen Produktionsvektor 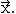   (5 BE)

3.3

Nach einer Umstellung des Produktionsverfahrens ist eine neue Inputmatrix gegeben durch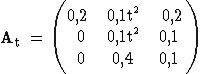
, dabei ist 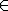t [0,5 ; 3] 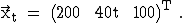ein reeller technologieabhängiger Parameter. Für die Produktion ist folgender Produktionsvektor geplant: Berechnen Sie den Wert von t, für welchen die Summe der Marktabgaben aller drei Zweigwerke am größten ist.   (6 BE)

Ermitteln Sie den Produktionsvektor.      (5 BE)

Skizzieren Sie das zugehörige Verflechtungsdiagramm ("Gozintograph"), wenn die Produktion von U 50 ME, die von V 40 ME und die von W 60 ME beträgt.       (7 BE)

In der nächsten Zeit soll bei unveränderter Inputmatrix die Produktion im Bereich W auf 80 ME gesteigert werden. Die Produktionen in den Bereichen U und V sollen so verändert werden, dass in beiden Bereichen die gleichen Mengen produziert werden. Berechnen Sie die in den Bereichen U und V möglichen Produktionsmengen.       (5 BE)

Gegeben ist folgendes Gleichungssystem mit:



Ermitteln Sie die Anzahl der Lösungen in Abhängigkeit von r.      (7 BE)

Im sind die Geraden g, h und i gegeben. Die Gerade g verläuft durch die Punkte und und die Gerade i durch die Punkte und . Weiter gilt: .

Zeigen Sie, dass die Geraden g und h echt parallel sind.      (3 BE)

Die Ebene F ist durch die Geraden g und h festgelegt. Ermitteln Sie eine Gleichung der Ebene F in Koordinatenform und beschreiben Sie deren besondere Lage im Koordinatensystem. (mögliches Teilerergebnis: )      (5 BE)